Развитие фрактальных моделей агрегации коллоидных частиц
Зырянов Роман Сергеевичмагистрант
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» имени В. И. Ульянова (Ленина)
В данной статье рассматриваются основные модели агрегации коллоидных частиц и становление представлений о фрактальной структуре агрегатов. Проведен обзор с момента введения термина фрактал Б. Мандельбротом до современных моделей агрегации.
Ключевые слова: фрактал, фрактальный агрегат, ограниченная диффузией агрегация, коллоид, фрактальная размерность, кластер-кластерная агрегация
Описать простыми геометрическими формами сложные фигуры, которые наблюдаются экспериментально на поверхности слоев, как правило, представляется бесперспективным. В то же время игнорировать появление иных форм симметрии, а именно фрактальных, на формирование окончательных электрооптических и термодинамических свойств неоправданно.
Применение фрактального анализа к описанию самоподобного состояниястак называемыми фрактальными, сложнымиформами симметрии в системах представляет собой одно из перспективных направлений в исследовании свойств пространства в наномире. Исходя из этого, для понимания того, как фрактальная геометрия вписывается в физические свойства материалов, надо проследить как зарождался термин фрактал и рассмотреть основные модели, описывающие физические фрактальные структуры в хронологическом порядке.
- Появление термина фрактал
На протяжении долгого времени считалось, что мелкие частицы, диспергированные в жидкостях и газах, могут образовывать агрегаты с низкой плотностью. В различных исследованиях в 1960-х и 1970-х годах, на основе компьютерных моделей было предположено, что «аномальные» масштабные отношения связанны со структурой этих агрегатов. Отсутствие подходящей теоретической базы и небольшая вычислительная мощность компьютерной техники тормозили развитие понимания структуры этих агрегатов и кинетики их образования. В 1980-е годы, популяризация фрактальной геометрии и быстрый прогресс в области компьютерных технологий устраняет эти препятствия. Термин «фрактал» введён Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальные объекты: форма, случайность и размерность» [1, с. 21].
- Модель Виттена-Сэндера идиффузионной агрегации
После получения экспериментального доказательств фрактальной структуры аэрозольных агрегатов, изображенных на рисунке 1, Форрестом и Виттеном в 1979 году, было сделано много попыток построения реалистичных теоретических моделей, позволяющих воспроизводить эти структуры [2, с. 110]. Пионерская модель была создана Томасом Виттеном и Леонардо Сэндером в 1981 году.

Рис. 1. Проекция фрактального кластера железа, полученная с помощью электронного микроскопа
Аналитические исследования, подтвержденные компьютерным моделированием, показывают, что «виттен-сэндеровские» агрегаты, изображенные на рисунке 2 [3, с. 5092], являются специальным видом самоаффинных фракталов с фрактальной размерностью, большей в радиальном направлении, чем в тангенциальном направлении, и что фрактальные размерности зависят от решетки [4, с. 1408].
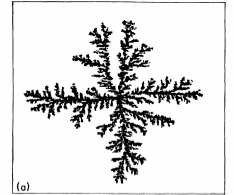
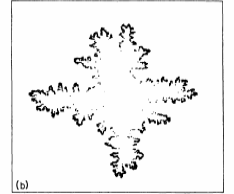
Рис. 2. а) кластер, состоящий из 4·106 частиц. б) места, где происходит рост кластера
П. Мекиным были проведены очень важные исследования по влиянию изменения фрактальной размерности траекторий частиц на фрактальную размерность кластера в рамках модели агрегации, лимитированной диффузией. Напомним, что фрактальная размерность траектории частицы Ds, совершающей броуновское движение, равна 2. При уменьшении Ds от 2 до 1 (баллистическая модель, прямолинейное движение) фрактальная размерность агрегата D возрастает и становится равной размерности пространства, иными словами объект перестает быть фракталом. Другая модель, в которой не рассматриваются какие-либо траектории вообще, — модель Айдена (1961 г), Ds = 0. На рисунке 3 продемонстрированы агрегаты при различных траекториях движения частиц. Для визуализации трехмерной модели агрегата можно использовать технологию трехмерной печати [5, с. 101].
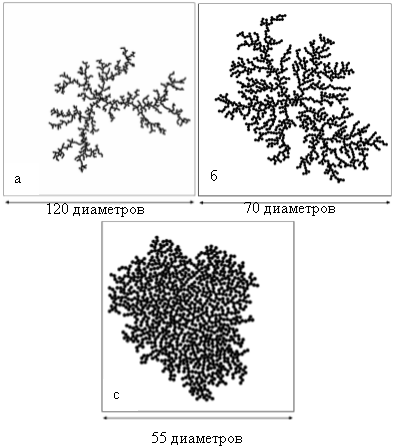
Рис. 3. а) траектория частицы — броуновское движение. б) траектория частицы — баллистическая. с) модель Айдена, частицы не двигаются
- Расширение модели Виттена-Сэндера. Кластер-кластерная агрегация
С тех пор как была реализована виттен-сэндеровская модель, стало понятно, что она не является наиболее приемлемой моделью агрегационных экспериментов на коллоидах и аэрозолях. Теоретические значения фрактальных размерностей (D ~ 2,5 3d) были слишком большими в сравнении с экспериментальными (D ~ 1,7 3d). Чтобы лучше описать эти эксперименты, была предложена альтернативная кластер-кластерная агрегационная модель, изображенная на рисунке 4, независимо и в одно и то же время в США [6, с. 1119] и во Франции [7, с. 1125]. Эта модель может рассматриваться как расширение виттен-сэндеровской модели, в которой сами кластеры могут двигаться вместе с частицами.
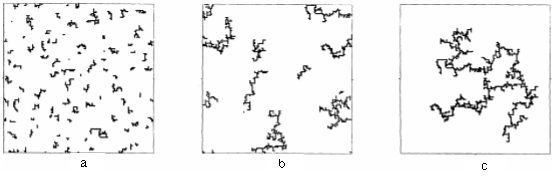
Рис. 3. Стадии роста при кластер-кластерной агрегации, а) 86 кластеров, б) 8 кластеров, с) 1 кластер
Идеализированная версия кластер-кластерной модели, иерархическая модель, которая была введена в 1971 [8, с. 2078], была снова высказана позднее [9, с. 75]. В этой модели следующие один за другим наборы кластеров из равного числа части: 2, 4, 8,..., 2k строятся последовательно. На каждом шагу кластеры группируются парами и один из кластеров может диффундировать в пространстве до соударения с другим. Модель основана на коагуляции Смолуховского.
Смолуховский, в 1916 г., предложил рассматривать процесс коагуляции как попарное слипание частиц, принимая вероятность одновременного столкновения трех частиц столь малой, что такие столкновения можно не учитывать.
При построении модели химически ограниченной кластер-кластерной агрегации (RLCA-модели) вводится понятие вероятности соединения, и затем эта вероятность устремляется к нулю. В этом пределе кластеры некоторое время «изучают» все возможные соединения и, в конце концов, выбирают одно случайное. Интерес к такой модели вызван тем, что она реализуется в коллоидах, когда электростатическое отталкивание не полностью экранировано. Фрактальная размерность в этом случае равна D ~ 2 при размерности пространства d = 3. Это больше, чем величина D ~ 1.78, полученная в чисто диффузионном случае (с вероятностью соединения равной единице). Такое изменение фрактальных свойств агрегатов близко к наблюдаемым в экспериментах.
- Дальнейшее усовершенствование моделей агрегации
Реструктуризация. Идея заключается в том, что при объединении двух кластеров обобщенная система еще не становится жесткой. Кластеры могут вращаться друг относительно друга вокруг точки соприкосновения. Необходимо образование второй, а для полной жесткости — и третьей связи [10, с. 1546].
Поляризация. Если два кластера находятся близко, то наводят заряды противоположного знака на ближайших друг к другу концах. В результате возникает взаимное электростатическое притяжение, оказывающее влияние на диффузионное движение и плотность (фрактальную размерность) конечного агрегата [11, с. 2133].
Изменение рН. Во многих практических случаях, часто встречающихся в промышленных процессах, агрегация заряженных коллоидов вызывается дополнительным введением противоположно заряженных ионов в коллоидный раствор. Представляется весьма важным моделирование таких механизмов. В первом приближении можно расширить кластер-кластерную модель на случай двух диффундирующих веществ, А (частицы) и В (полимеры), в которой связи А–В разрешены, а А–А и В–В — подавлены [12, с. 2139].
Открытие того, что агрегаты коллоидных частиц имеют фрактальную природу, было важным шагом для становления представлений о золь-гель процессах, теории перколяции и сенсорики [13. с, 22]. Появились новые методы оценки поверхности вещества, взаимосвязь между поверхностной структурой и различными термодинамическими свойствами вещества.
Литература:
- Mandelbrot B. Fractals: form, chance and dimension. — San Francisco: WH Freeman & Co., 1979. — 365 с.
- Forrest S. R., Witten Jr T. A. Long-range correlations in smoke-particle aggregates //Journal of Physics A: Mathematical and General. — 1979. — Т. 12. — №. 5. — С. L109.
- Meakin, P., Ramanlal, P., Sander, L. M., & Ball, R. C. Ballistic deposition on surfaces //Physical Review A. — 1986. — Т. 34. — №. 6. — С. 5091.
- Ball, R. C., Brady, R. M., Rossi, G., & Thompson, B. R. Anisotropy and cluster growth by diffusion-limited aggregation //Physical review letters. — 1985. — Т. 55. — №. 13. — С. 1406.
- Зырянов Р. С. Получение слоев функциональных материалов из жидкой фазы методами трехмерной печати // Молодой ученый. — 2016. — № 6. — С. 101–105.
- Meakin P. Formation of fractal clusters and networks by irreversible diffusion-limited aggregation //Physical Review Letters. — 1983. — Т. 51. — №. 13. — С. 1119.
- M. Kolb, R. Botet, and R. Jullien Scaling of Kinetically Growing Clusters //Physical Review Letters. — 1983. — Т. 51. — №. 13. — С. 1123.
- Sutherland D. N., Goodarz-Nia I. Floc simulation: the effect of collision sequence //Chemical Engineering Science. — 1971. — Т. 26. — №. 12. — С. 2071–2085.
- Botet R., Jullien R., Kolb M. Hierarchical model for irreversible kinetic cluster formation //Journal of Physics A: Mathematical and General. — 1984. — Т. 17. — №. 2. — С. L75.
- Meakin P., Jullien R. Structural readjustment effects in cluster-cluster aggregation //Journal de Physique. — 1985. — Т. 46. — №. 9. — С. 1543–1552.
- Jullien R. A new model of cluster aggregation //Journal of Physics A: Mathematical and General. — 1986. — Т. 19. — №. 11. — С. 2129.
- Meakin P., Djordjevic Z. B. Cluster-cluster aggregation in two-monomer systems //Journal of Physics A: Mathematical and General. — 1986. — Т. 19. — №. 11. — С. 2137.
- Александрова. О. А., Алешин А. Н., Белорус А. О. и др. Новые наноматериалы. Синтез. Диагностика. Моделирование: лаб. практикум. / Под ред. Мошников В. А., Александрова О. А. — СПб.: Издательство СПбГЭТУ «ЛЭТИ». — 2015. — 248 с.

