В статье авторы рассматривают моделирование пространственной стержневой системы с помощью методов вычислительного дизайна. Исследуют применимость алгоритмического проектирования в задачах моделирования однослойных стержневых оболочек с треугольным делением решетки.
Ключевые слова: вычислительный дизайн, вариантное проектирование, стержневая система, пространственные конструкции, поиск формы, визуальное программирование.
Архитектурная концепция
Вычислительный дизайн — это динамически развивающийся метод проектирования, в котором вместо того, чтобы выполнять задачу, исходя из доступных инструментов (программ), проектировщик сам разрабатывает инструмент, исходя из задачи.
Подобная методика может быть крайне эффективна в строительной отрасли при проектировании сложных многовариантных конструкций. В данной работе мы будем рассматривать проектирование пространственной однослойной стержневой модели (оболочки) по заданным архитектурным требованиям и контурам, с помощью разработанных в ходе работы алгоритмов и физических симуляций.
Основные требования, продиктованные архитектурной концепцией:
– материал стержней сосна, сечение круглое в диаметре не более 30 мм;
– длины отдельных стержневых элементов не должны превышать 1 м;
– решетка пространственной системы — треугольная;
– высота конструкций покрытия не должна превышать 1,5 м;
– опорные элементы разместить по осевой линии парапета;
– конструкция внутри теплого контура.
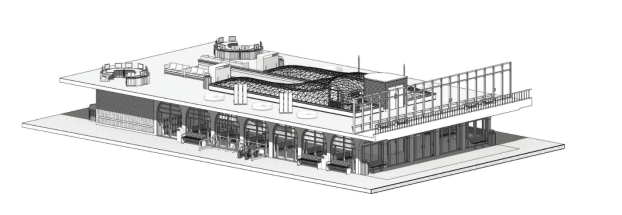
Рис. 1. Архитектурная концепция пространственного покрытия
В качестве базового инструментария будем использовать графический программный комплекс Rhinoceros и систему визуального программирования Grasshopper
Суть метода наследует принципы, выдвинутые Р. Гуком и исследованные А. Гауди [1,2] в рамках поиска рациональных форм плоских арочных систем (цепная линия). А также методы, разработанные в ходе поиска формы пространственных растянутых и сжатых структур в Германии О. Фраем и Дж. Шеком [3, 4, 5, 6]. В работе предлагается провести математический эксперимент, основанный на физической симуляции провисания плоской поверхности, закрепленной по контуру. В результате реверса деформированной схемы поверхности мы получим наиболее рациональную (испытывающую сжатие) форму оболочки в пространстве.
Моделирование пространственной системы с помощью вычислительного дизайна
Перед началом работы по моделированию стержневой системы нам необходимо преобразовать имеющиеся исходные данные. Для этого импортируем контур, по которому требуется разместить проектируемую оболочку в формате.dwg в файл проекта Rhinoceros. Предполагается что данный контур отчерчивает срединную линию железобетонных стен, на которые происходит опирание оболочки. Следующей задачей будет размещение опорных точек, которые будут служить, как местами для размещения опорных узлов, так и граничными условиями при дальнейшем статическом расчете. Деление будем производить с помощью системы визуального программирования Grasshopper, предварительно подгрузив в нее участки контура. Именно эта операция будет служить отправной точкой при создании алгоритма, генерирующего пространственную стержневую систему. Стоит отметить, что среда Grasshopper работает с геометрией, имеющейся в файле Rhinoceros, при этом никаким образом не изменяя ее. То есть, любой существующий в файле объект, может служить опорой для алгоритма. Остальные объекты, которые производятся с помощью самого алгоритма в файле не существуют, а являются надстройкой над опорными объектами. Это позволяет изменять или заменять участки контура, по которому предполагается размещение оболочки, обеспечивая инвариантность и воспроизводимость алгоритма для любого контура. Схема деления имеющегося контура представлена на рис. 2.
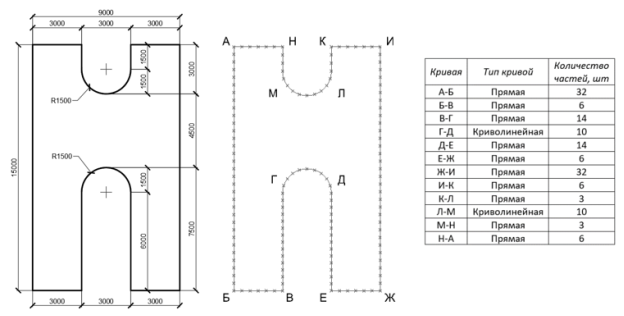
Рис. 2. Импорт контура опирания оболочки в среду Rhinoceros. Деление кривых на участки
Полученные точки и отрезки, используем для построения поверхности, вписанной в данный контур. Подобное вспомогательное построение необходимо для преобразования поверхности в полигональную сетку (polygon mesh), а именно совокупность ребер, граней и вершин, представляющих форму объекта в трехмерной среде. В основном преобразование поверхности или трехмерного объекта в полигональную сетку производиться для упрощения геометрии и уменьшения излишней сложности модели. Представление объекта происходит в виде совокупности простых выпуклых многоугольников (в основном треугольников и четырехугольников). В нашем случае по поверхности простраивается произвольная полигональная сеть, состоящая из треугольников, имеющих свои вершины во всех ранее заданных точках. Подобную хаотичную сеть необходимо привести к структурированной постепенно уменьшая размер граней и увеличивая их количество. Данная операция носит название подразделение (subdivision) в общем смысле включая в себя и предыдущий этап, а именно разделение поверхности на полигоны. В данном случае мы будем работать не с поверхностью, а с совокупностью уже имеющихся граней полигональной сети, дробя их на субэлементы. Процесс начинается с исходной полигональной сети, алгоритм работает с уже известными гранями и вершинами, добавляя новые грани и вершины на их основе. Положение изначальных вершин в различных методах может либо меняться, либо оставаться фиксированным. В нашем случае мы используем плагин Mesh Machine основанный на методе Loop Subdivision в ходе выполнения которого, положение исходных вершин может быть скорректировано. При этом, позиции опорных точек являются определенными, фиксированными и при дальнейшем делении будут неподвижны. Информация о фиксированных ребрах, вершинах и другая входная информация (примерный размер ребра, сила натяжения сети, количество итераций) вносится в исходные данные плагина.
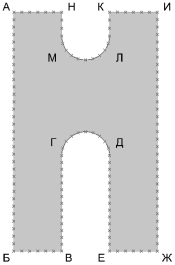
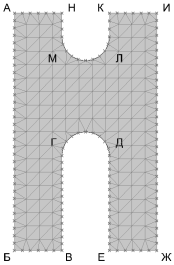
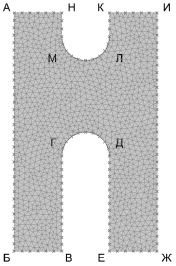
Рис. 3. Первичная поверхность. Черновая полигональная сетка. Исходная полигональная сетка
В нашем случае полигональная сетка является исходной для физической симуляции. Симуляция физических процессов будет происходить с использованием плагина Kangaroo. К закрепленной по контуру оболочке будут приложены силы обратные гравитации с поправочным коэффициентом, дополнительно будет дано начальное натяжении по поверхности оболочки (аналогия с силами поверхностного натяжения). При подобном воздействии оболочечная конструкция с деформируется и образует равновесную форму для заданного поправочного коэффициента, приложенных гравитационных сил и сил поверхностного натяжения. При этом количество форм равновесия напрямую зависит от комбинаций входных параметров.
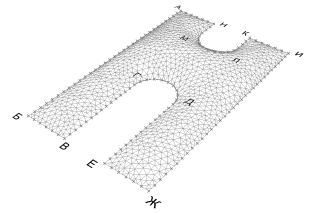
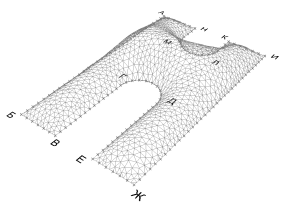
Рис. 4. Поиск формы оболочки с помощью физического движка Kangaroo. Финальная форма
Для дальнейшей работы выделим форму, которая наиболее соответствует архитектурными требованиями (выпуклостью, размерами элементов) и будем считать ее финальной. Обозначим вышеперечисленные параметры характеризующую данную форму:
Таблица 1
Параметры исходной пространственной стержневой системы
|
Номер конструкции |
Исходные параметры | |||
|
Размер грани конечного элемента, - |
Сила натяжения, - |
Количество итераций, шт. |
Величина прилагаемой силы, - | |
|
Финальный |
0,29 |
0,45 |
15 |
49,86 |
Алгоритм поиска формы
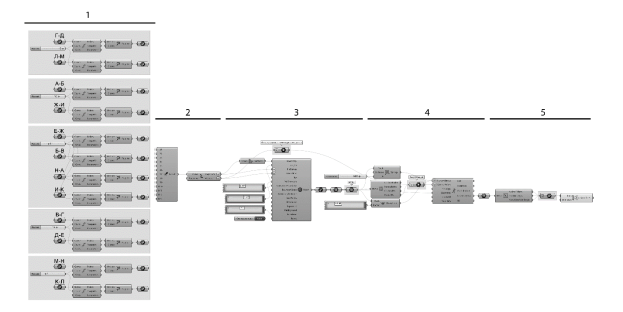
Рис. 5. Алгоритм поиска формы пространственной стержневой системы с помощью физической симуляции в среде Rhinoceros, Grasshopper с использованием плагинов Mesh Machine и Kangaroo
В результате работы в системе визуального программирования Grasshopper был разработан алгоритм, упрощающий процесс поиска формы оболочечных конструкций с помощью физической симуляции. Алгоритм состоит из нескольких информационных блоков:
- Подгрузка геометрии в алгоритм из рабочего файла Rhinoceros. Деление кривых на заданное количество частей, определение опорных точек.
- Объединение всех полученных сегментов и точек контура в единый список. Построение поверхности по заданному контуру.
- Работа с полигональной сеткой по входным параметрам, получение полигональной сети, находящейся в одной плоскости.
- Задание исходных параметров для физической симуляции — определение граничных условий, силы натяжения и прилагаемой пространственной силы.
- Извлечение ребер из полигональной сети, удалении дублирующихся стержней.
Подобная структура алгоритма позволяет вносить любые изменения в процессе работы над формой стержневой системы. При этом для одного контура могут быть получены различные формы равновесия, они характеризуются внешними силовыми факторами (сила натяжения, сила гравитации). Так же стоит отметить, что созданный алгоритм способен создавать подобный тип конструкции для любой площади и основы (контура) и может быть использован многократно.
Выводы
В ходе работы были реализованы основные принципы вычислительно дизайна, а именно разработка конкретного инструмента под выполнение конкретной задачи. Была получена наиболее рациональная форма пространственной однослойной оболочки, где основными усилиями, возникающими в стержнях, являются продольные силы сжатия. Подобный алгоритм позволяет создавать подобные оболочки над любыми опорными контурами. Основным преимуществом данного метода перед ранее разработанными является простота использования, а также возможность экспорта в программы для конечно-элементного расчета (SCAD, Лира и т. п.). Подобный алгоритм может быть доработан с помощью инструментов генетической или иной оптимизации позволяющих среди тысяч форм равновесия найти наиболее благоприятную, например менее материалоемкую. Положительное влияние также может оказать добавление модуля конечно-элементного анализа способного мгновенно производить оценку прочности стержневой системы.
Литература:
- Цепная линия. Идеальная арка от природы. Текст: электронный // ArtElectronics: [сайт]. — URL: https://artelectronics.ru/blogs/tsepnaya-liniya-idealnaya-arka-ot-prirody (дата обращения: 02.05.2020).ASTM. 1986. Standard specification for evaluating performance of prefabricated wood I-joists. Draft (7/88). American Society for Testing and Materials, Philadelphia, PA. 60 pp.
- Vizotto, I. Computational generation of free-form shells in architectural design and civil engineering. Automat Constr 2010; 19: 1087–1105.
- Wu, J, Burgueño, R. An integrated approach to shape and laminate stacking sequence optimization of free-form FRP shells. Comput Method Appl M 2006; 195: 4106–4123
- Frei Otto and the development of gridshells. Текст: электронный // ScienceDirect: [сайт]. — URL: https://www.sciencedirect.com/science/article/pii/S2214399815300011 (дата обращения: 02.05.2020). [5] Bletzinger, KU, Ramm, E. Structural optimization and form finding of light weight structures. Comput Struct 2001; 79: 2053–2062
- Balz, M, Böhm, J. Generating shell models and their realization by photogrammetric measurement. In: Shell and spatial structures from models to realization, IASS 2004 symposium, Montpellier, 20–24 September 2004, paper no. TP119. CD-ROM of IASS

