В статье автор исследует особенности и проблемы трассировки лучей на неструктурированную расчетную сетку.

Ключевые слова: луч, трассировка лучей, неравномерная объемная сетка, ячейка, иерархическая сетка.

Эффективная трассировка лучей через сложные среды требует оптимизации пространственного разбиения для повышения вычислительной производительности и точности моделирования.

Цель данной работы — исследовать и сравнить методы применения равномерных и иерархических сеток для трассировки лучей, а также изучить возможности неравномерных объемных сеток для повышения эффективности расчетов в задачах с поглощающей и излучающей средой.

В статье рассматриваются методы равномерного и иерархического разбиения вычислительной области с использованием ограничивающих объемов, а также применение неравномерных объемных сеток. Анализируются их эффективность в зависимости от распределения объектов и количество вычислительных ресурсов, необходимых для обработки пересечений лучей с объектами.

Равномерная и иерархическая сетка

Применение сетки для трассировки лучей включает разбиение вычислительной области на равные интервалы, образующие равномерную сетку внутри ограничивающего параллелепипеда. Каждая ячейка сетки содержит список ограничивающих объемов, и луч последовательно просматривает каждую ячейку. Объекты в каждой ячейке проверяются на пересечение с лучом, и процесс завершается при первом обнаружении пересечения (см. рис. 1).

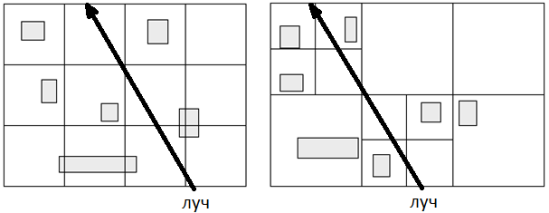
Рис. 1. Примеры равномерной и иерархической сеток

В случае равномерного распределения объектов метод сетки эффективен, но при неравномерном распределении может возникнуть неэффективность из-за избыточных проверок или множества пустых ячеек. В таких случаях используются иерархические сетки, которые разделяют область на равномерные ячейки, а затем только ячейки с наибольшим количеством объектов дополнительно разбиваются, что позволяет ускорить алгоритм.

Рассмотрим процесс трассировки луча через такую иерархическую сетку. Луч начинает свой путь с корневой ячейки и, проходя через ячейки верхних уровней иерархии, проверяет на пересечение только те из них, которые содержат объекты. Если луч входит в ячейку, которая делится на ячейки меньшего размера, то он рекурсивно продолжает свой путь через них, пока не достигнет самого нижнего уровня и перейдет к следующей ячейке уровня выше или пока не будет найдено пересечение с объектом.

Основное преимущество иерархической сетки заключается в её способности адаптироваться к сценам с высокой сложностью и неоднородным распределением объектов, снижая количество проверок и улучшая время выполнения алгоритма трассировки лучей. Однако, стоит отметить, что создание иерархической сетки может быть сложным и требовать дополнительных вычислительных ресурсов для её построения и управления.

Неравномерная объемная сетка

Неравномерная объемная сетка — это метод пространственного разбиения, где ячейки зачастую имеют форму тетраэдра или.

Данный метод позволяет моделировать среды и объекты как бы подменяя их ячейками сетки с требуемыми свойствами. Это значит, что ячейки не содержат исследуемые объекты (пустое пространство, твердые объекты, газы), а моделируют их физические и геометрические свойства с заданной точностью.

Таким образом, при пересечении грани соседних ячеек, луч либо попадает в другую среду, либо продолжает движение по текущей среде. Соответственно, на каждом шаге задача состоит в определении грани которую пересекает луч и определения следующей ячейки, в которую он попадает. В общем случае, если луч пересекает грань твердого тела, то его трассировка завершается [4].

Этот подход обеспечивает высокое качество аппроксимации геометрии объекта и упрощает алгоритмы поиска пересечений с гранями ячеек [1]. Однако он ограничивает возможность решения проблемы неравномерной концентрации объектов, что приводит к обработке большого числа однородных соседних ячеек, в том числе и пустых. Несмотря на потенциал, алгоритмы в этой области все еще нуждаются в разработке и имеют существенные недостатки (см. рис. 2).

Рис. 2. Примеры неравномерной сетки — структурированная четырехугольная сетка на рисунке слева и неструктурированная треугольная сетка справа [2]

В случае трассировки лучей в поглощающей среде необходимо учитывать не только поверхность, с которой столкнулся луч, но и все прозрачные грани сеточной модели, через которые луч прошел. Это необходимо для вычисления длины луча, пройденной через каждую объемную зону модели, и определения доли поглощенной энергии в каждой зоне.

Метод использования неравномерной объемной сетки позволяет легко определить все грани, через которые прошел луч. Следовательно, применение неравномерной объемной сетки в качестве структуры данных для ускорения трассировки лучей в задачах моделирования физических процессов с применением неструктурированных расчетных сеток является наиболее перспективным.

Неравномерные объемные сетки также позволяют более точно учитывать сложные физические явления, такие как диффузия, конвекция и поглощение энергии в различных материалах. В моделях с высокой степенью сложности, таких как симуляции атмосферных явлений, биологических тканей или сложных технических объектов, неравномерные сетки позволяют достигать необходимой детализации без существенного увеличения вычислительных затрат. Они также облегчают адаптацию моделей к изменяющимся условиям, таким как движение объектов или изменение их физических свойств во времени.

На данный момент в сферах, таких как компьютерная графика, медицинская визуализация и инженерное проектирование, использование неравномерных объемных сеток становится стандартом. Это связано с их способностью точно моделировать сложные геометрические и физические свойства объектов, обеспечивая при этом высокую эффективность вычислений. В дальнейшем, развитие методов генерации и оптимизации неравномерных объемных сеток, а также улучшение алгоритмов трассировки лучей, работающих с такими сетками, будет способствовать созданию еще более точных и реалистичных моделей.

Выводы

Применение иерархических сеток показало значительное улучшение в вычислительной эффективности при неравномерном распределении объектов по сравнению с равномерными сетками. Неравномерные объемные сетки обеспечивают высокое качество аппроксимации геометрии и упрощают алгоритмы поиска пересечений, что особенно важно для задач с поглощающей средой, где необходимо учитывать все прозрачные грани, через которые проходит луч.

Использование иерархических сеток и неравномерных объемных сеток является перспективным направлением для оптимизации трассировки лучей в сложных средах. Эти методы позволяют уменьшить количество избыточных проверок и повысить точность моделирования, что особенно важно в задачах, связанных с моделированием физических процессов в поглощающих и излучающих средах.

Литература:

1. Г. К. Маликов, В. Г. Лисиенко, Р. П. Коптелов. Методы трассировки лучей для определения угловых коэффициентов излучения в промышленных сложных геометриях. // Известия вузов. Черная металлургия. — 2010. — N 7. — С. 53–59.
2. М. П. Галанин, В. В. Лукин. Разностная схема для решения двумерных задач идеальной МГД на неструктурированных сетках // Препринт ИПМ им. М. В. Келдыша РАН, 2007, № 50.