Сложный процент — это экономическая категория, используемая для сопоставления одной и той же суммы денег в различные периоды времени с учетом того, что в каждом периоде доход приносит не только первоначально вложенная сумма, но и процент от нее [1, c. 11].
Смысл сложного процента заключается в том, что проценты, начисленные в конце каждого периода, не выплачиваются, а присоединяются к основной сумме вложенного капитала, и в следующий расчетный период процент начисляется уже на большую сумму.
В рамках доходного подхода при использовании собственного капитала инвестора применяются два метода определения стоимости оцениваемого объекта недвижимости, в которых используются функции сложного процента — это метод капитализации по расчетным моделям и метод дисконтирования денежных потоков (ДДП).
Наиболее универсальным методом определения текущей стоимости оцениваемой недвижимости является метод ДДП. В учебнике «Оценка недвижимости» [2, с.163] предлагается рассчитывать стоимость объекта недвижимости методом ДДП по формуле
![]() (1)
(1)
где ![]() текущая стоимость;
текущая стоимость; ![]() денежный поток периода
денежный поток периода ![]() ;
; ![]() ставка дисконтирования денежного потока периода
ставка дисконтирования денежного потока периода ![]() ;
; ![]() стоимость реверсии, или остаточная стоимость.
стоимость реверсии, или остаточная стоимость.
В формуле (1) знаменатель первого и второго слагаемых представляет собой общую формулу сложного процента, которая используется в его шести функциях. Величину ![]() в финансовых расчетах называют множителем наращения по сложным процентам, фактором будущей стоимости единицы, коэффициентом наращения, а обратную ей величину
в финансовых расчетах называют множителем наращения по сложным процентам, фактором будущей стоимости единицы, коэффициентом наращения, а обратную ей величину ![]()
![]() — дисконтным, или дисконтирующим множителем. В теории оценки общую формулу сложного процента называют будущей стоимостью единицы, а обратную ей величину — текущей стоимостью единицы или коэффициентом дисконтирования.
— дисконтным, или дисконтирующим множителем. В теории оценки общую формулу сложного процента называют будущей стоимостью единицы, а обратную ей величину — текущей стоимостью единицы или коэффициентом дисконтирования.
Базовой функцией сложного процента является первая функция — будущая стоимость капитала. В работе «Элементы финансовой математики (курс лекций и сборник задач)» формула будущей стоимости капитала имеет следующий вид [3, c. 7–8]
![]() (2)
(2)
где ![]()
![]() будущая стоимость капитала;
будущая стоимость капитала; ![]() текущая стоимость (стоимость в начальный момент времени);
текущая стоимость (стоимость в начальный момент времени); ![]() ставка процента, начисляемого периодически;
ставка процента, начисляемого периодически; ![]() количество периодов начисления (год, квартал, месяц, день).
количество периодов начисления (год, квартал, месяц, день).
Остальные пять функций сложного процента — это производные от первой функции сложного процента (будущей стоимости капитала). В теории и практике оценки стоимости недвижимости методом ДДП используется четвертая функция сложного процента, которая является обратной первой функции и имеет следующий вид
![]() (3)
(3)
где ![]() будущая стоимость капитала;
будущая стоимость капитала; ![]() ставка дисконтирования будущей стоимости капитала;
ставка дисконтирования будущей стоимости капитала; ![]() количество периодов дисконтирования будущей стоимости капитала.
количество периодов дисконтирования будущей стоимости капитала.
Ключевым параметром сложного процента является ставка процента (процентная ставка), которая с математической точки зрения выражает численное значение (в форме процентов или десятичной дроби). В практических финансовых расчетах процентные ставки обычно измеряются в десятичных дробях. В учебнике по финансовой математике Е. М. Четыркина указано, что «временной интервал, к которому приурочена процентная ставка, называют периодом начисления, его не следует путать со сроком начисления» [4, c. 17]. Из данного положения следует, что процентная ставка имеет не только числовое значение, но и временную характеристику.
Однако в [3] и в литературе по оценке стоимости недвижимости временной интервал (период начисления) ставки процента в общей формуле сложного процента, как правило, не указывается. В этой связи ставка процента выступает в общей формуле сложного процента как безразмерная величина и поэтому может суммироваться с единицей, что нельзя признать правомерным.
Временные единицы измерения ставки процента приводятся в учебной литературе по финансовой математике. Так, например, в учебном пособии «Финансовая математика» [5, c. 8] приведены переводы единицы измерения ставки процента: «Иногда полезно переводить процентные ставки из одной единицы измерения в другую. Для этого достаточно сделать переход к другим единицам измерения времени. Так, например, если дана годовая процентная ставка ![]() (1/год), то месячная процентная ставка равна
(1/год), то месячная процентная ставка равна ![]() и т. д».
и т. д».
Временная характеристика ставки процента присуща ей и она не сокращается под влиянием какого-либо фактора. Но тогда возникает проблема реализации общей формулы сложного процента, так как по правилам математики нельзя выполнять суммирование единицы с параметром, имеющим единицу измерения, т. е. некорректно складывать безразмерную величину (единицу) со ставкой процента, являющейся размерной величиной, например, ![]() , если 0,12 — численное значение годовой ставки процента. В этой связи нельзя признать правомерным суммирование единицы с размерной ставкой процента в формуле (2).
, если 0,12 — численное значение годовой ставки процента. В этой связи нельзя признать правомерным суммирование единицы с размерной ставкой процента в формуле (2).
Кроме того, нельзя в формуле (2) признать правомерным указанные единицы измерения параметра «Количество периодов начисления процентов» — год, квартал, месяц, день. По правилам математики нельзя возводить число или какой-либо показатель в степень, которая имеет числовое значение и единицу измерения, т. е. не является безразмерным показателем.
Целью настоящей статьи является исправление недостатков формулы сложного процента для корректного с математической точки зрения ее применения в теории оценки стоимости недвижимости.
Как известно, сложный процент является дальнейшим развитием простого процента, который выражается формулой
![]() (4)
(4)
где ![]() ставка процента, 1/год;
ставка процента, 1/год; ![]() срок начисления процентов, годы.
срок начисления процентов, годы.
Смысл простого процента заключается в том, что процент начисляется только на первоначальный капитал, а полученная постоянная величина прибыли не участвует в обороте капитала и ее можно использовать после окончания каждого отчетного периода.
В формуле (4) нет нарушений правил математики, так как при умножении ставки процента в форме десятичной дроби на срок начисления процентов, выраженных в одинаковых единицах времени, происходит сокращение этих единиц измерения. В результате умножения ставки процента на срок начисления процентов получается безразмерная величина, которая может суммироваться с единицей в общей формуле простого процента. Простой процент можно использовать и в методе ДДП без нарушения правил математики.
Переход от простого процента к сложному проценту в финансовой математике иллюстрируется на примере инвестора, который по депозитному договору с банком вложил определенную сумму денежных средств на депозитный счет на определенный срок с начислениями по простому проценту. После получения вложенной суммы денег с начисленными процентами инвестор перезаключил договор с банком на следующий такой же срок с начислениями по простому проценту. Число перезаключений депозитного договора инвестора с банком может быть многоразовое, что означает реинвестирование средств, полученных на каждом этапе наращения с помощью постоянной или переменной ставки процента.
Схема наращения денежных средств инвестора по простому проценту в результате перезаключений договоров (реинвестирования средств), например для трех реинвестирования средств, будет иметь следующий вид
![]() (5)
(5)
В общем виде формула наращения (5) при годовой процентной ставке, сроке начисления, измеряемого в годах, многократном реинвестировании средств будет иметь вид
![]() (6)
(6)
где ![]() ставка процента, 1/ год;
ставка процента, 1/ год; ![]() срок начисления процентов, годы;
срок начисления процентов, годы; ![]() количество повторений реинвестирования, в течение общего срока реинвестирования средств.
количество повторений реинвестирования, в течение общего срока реинвестирования средств.
Если в формуле (6) срок начисления процентов (![]() ) у всех перезаключаемых договоров принять равным одному периоду (одному году, одному полугодию, одному кварталу, одному месяцу и т. д. или определенному числу дней в пределах года), то в этом случае
) у всех перезаключаемых договоров принять равным одному периоду (одному году, одному полугодию, одному кварталу, одному месяцу и т. д. или определенному числу дней в пределах года), то в этом случае ![]() будет выражать один период начисления процентов в течение заданного общего срока реинвестирования средств. Такой вид наращения будет представлять собой наращение по сложным процентам. Поэтому «наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая прослужила базой для их начисления, частоназывают капитализацией процентов» [4, c. 44].
будет выражать один период начисления процентов в течение заданного общего срока реинвестирования средств. Такой вид наращения будет представлять собой наращение по сложным процентам. Поэтому «наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая прослужила базой для их начисления, частоназывают капитализацией процентов» [4, c. 44].
В формуле (6) как и в формуле (4) произведение ![]() является безразмерной величиной тогда, когда знаменатель ставки процента и числитель одного периода начисления имеют одинаковые единицы измерения, которые при умножении сокращаются. Поэтому математически правомерно в множителе наращения складывать единицу с безразмерным произведением
является безразмерной величиной тогда, когда знаменатель ставки процента и числитель одного периода начисления имеют одинаковые единицы измерения, которые при умножении сокращаются. Поэтому математически правомерно в множителе наращения складывать единицу с безразмерным произведением ![]() .
.
Если заданный период начисления меньше годового периода ставки процента, то в этом случае годовой период ставки процента переводится в измеритель заданного периода начисления. Например, если заданный период начисления составляет 1 мес., тогда годовой период ставки процента должен выражаться в месяцах. В этом случае знаменатель годовой ставки процента будет равен 12 месяцам. При численном значении ставки процента равной 0,12 и периоде процентной ставки равном 12 мес., получим скорректированное значение ставки процента — 0,12/12 мес.=0,01/мес. Тогда произведение ![]() будет представлять коэффициент наращения первоначальной суммы вклада за 1 мес., который можно суммировать с единицей дисконтного множителя, как две безразмерные величины (1+0,01=1,01).
будет представлять коэффициент наращения первоначальной суммы вклада за 1 мес., который можно суммировать с единицей дисконтного множителя, как две безразмерные величины (1+0,01=1,01).
Параметр ![]() в формуле (6) может быть рассчитан по формуле
в формуле (6) может быть рассчитан по формуле
![]() (7)
(7)
где ![]() общий срок реинвестирования средств, выраженный в единицах времени одного заданного срока начисления.
общий срок реинвестирования средств, выраженный в единицах времени одного заданного срока начисления.
Рассчитаем значение ![]() для представленного выше примера, если
для представленного выше примера, если ![]() , что составляет 36 мес.
, что составляет 36 мес. ![]()
![]() Тогда
Тогда ![]()
В целом для данного примера значение множителя наращения по сложным процентам составит ![]()
В теории оценки стоимости недвижимости формула (6) будет иметь вид
![]() (8)
(8)
где ![]() будущая стоимость денежного потока;
будущая стоимость денежного потока; ![]() ставка дисконтирования денежного потока
ставка дисконтирования денежного потока ![]() периода;
периода; ![]() один заданный период дисконтирования денежных потоков (1 год, 1 полугодие, 1 квартал, 1 месяц или определенное число дней в пределах года);
один заданный период дисконтирования денежных потоков (1 год, 1 полугодие, 1 квартал, 1 месяц или определенное число дней в пределах года); ![]() количество временных интервалов (периодов) от дисконтируемого денежного потока до даты оценки.
количество временных интервалов (периодов) от дисконтируемого денежного потока до даты оценки.
На основе данных формулы (8) получим усовершенствованную модель оценки стоимости недвижимости методом ДДП
![]() (9)
(9)
где ![]() текущая стоимость, ден. ед.;
текущая стоимость, ден. ед.; ![]() наименование временного интервала прогнозного периода;
наименование временного интервала прогнозного периода; ![]() количество временных интервалов в прогнозном периоде;
количество временных интервалов в прогнозном периоде; ![]() денежный поток
денежный поток ![]() го временного интервала прогнозного периода, ден. ед.;
го временного интервала прогнозного периода, ден. ед.; ![]() ставка дисконтирования денежного потока
ставка дисконтирования денежного потока ![]() периода, 1/временной интервал;
периода, 1/временной интервал; ![]() один заданный период дисконтирования денежных потоков, временной интервал;
один заданный период дисконтирования денежных потоков, временной интервал; ![]() стоимость реверсии недвижимости в конце прогнозного периода, ден. ед.
стоимость реверсии недвижимости в конце прогнозного периода, ден. ед.
Для практических оценочных расчетов целесообразно в формуле (9) вместо параметра ![]() использовать соотношение срока прогнозного периода к заданному периоду дисконтирования денежных потоков
использовать соотношение срока прогнозного периода к заданному периоду дисконтирования денежных потоков ![]() Тогда модель оценки стоимости недвижимости методом ДДП будет иметь вид
Тогда модель оценки стоимости недвижимости методом ДДП будет иметь вид
![]() (10)
(10)
где ![]() значение прогнозного периода, ед. времени.
значение прогнозного периода, ед. времени.
В работе [6] отмечалось, что ставка дисконтирования должна включать не только временной интервал, но иметь в числителе и знаменателе еще и денежные единицы. Например, при годовом значении ставки дисконтирования равном 0,12, периоде дисконтирования равном году и денежного выражении числителя и знаменателя в рублях, ставка дисконтирования будет иметь наиболее общий вид ![]() .
.
При умножении ставки дисконтирования на один заданный период дисконтирования (год) происходит сокращение временных и денежных единиц измерения этих параметров и ставка дисконтирования превращается в коэффициент, который можно складывать с единицей в дисконтном множителе.
Кроме указанных выше недостатков формулы (1), следует отметить несопоставимость результатов дисконтирования текущих будущих денежных потоков и остаточной стоимости недвижимости. Так как при дисконтировании текущего будущего дохода каждого временного интервала периода владения будем получать приведенный денежный поток, а не текущую стоимость. Тогда как при дисконтировании остаточной стоимости недвижимости получим текущую стоимость, которую нельзя суммировать с суммарным приведенным денежным потоком из-за другой размерности. Например, при использовании годовых временных интервалов в прогнозном периоде и рублевом исчислении денежных потоков и остаточной стоимости получим размерность текущей стоимости объекта недвижимости вида ![]() .
.
Несопоставимость результатов дисконтирования денежных потоков объясняется тем, что будущие доходы от сдачи объекта недвижимости в аренду и остаточная стоимость недвижимости в конце прогнозного периода характеризуются разными по природе экономическими показателями, т. е. являются разнородными показателями.
Так, будущие доходы от сдачи объекта недвижимости в аренду на определенный период времени характеризуются показателями, которые в экономической науке называются интервальными экономическими показателями, т. е. численные значения показателей устанавливаются за определенный период времени. В оценке стоимости недвижимости временными периодами сдачи объекта в аренду чаще всего являются месяц или год. Если, например, объект сдается в аренду на год с месячными платежами, то при дисконтировании этих платежей (доходов) с размерностью руб./мес., их можно суммировать за год, получая размерность руб./год. И эти доходы не превращаются в текущую стоимость недвижимости. Их размерность такой же и останется, т. е. руб./год.
Остаточная стоимость объекта недвижимости представляет собой продажу объекта в конце периода владения (прогнозного периода). Выражается показателем, который характеризует стоимостное состояние объекта на определенный момент времени. Такой вид показателей в экономической науке называются моментными экономическими показателями. Поэтому при продаже объекта недвижимости его размерность будет выражена только в рублях на конец прогнозного периода. При дисконтировании моментного экономического показателя получаем его размерность в рублях.
Из-за разной размерности нельзя складывать интервальные показатели с моментными показателями, как это сейчас делается в теории оценки недвижимости, так как это противоречит правилам математики и экономическому смыслу.
В экономической науке, в частности экономической статистике, моментные и интервальные показатели трактуются следующим образом.
Моментные показатели характеризуют изучаемые социально-экономические процессы и явления по состоянию на определенную дату, начало или конец месяца, года, т. е. на определенный момент времени. К таким показателям относится численность населения, стоимость основных фондов, дебиторская задолженность и другие.
Интервальные показатели позволяют получать значения признаков за определенный период — день, неделю, месяц, квартал, год (производство продукции, число заключенных браков, сумма страховых выплат).
Отличительной особенностью интервальных показателей является возможность их суммирования. Например, суммируя производство продукции по месяцам, мы получаем общий объем производства за год.
Для устранения указанного недостатка формулы (1) автор в работах [6, 7] предложил вместо метода ДДП применить метод накопления денежных доходов (метод НДД). Сущность метода НДД заключается в том, что текущие денежные доходы от эксплуатации объекта недвижимости в конце каждого расчетного периода передаются на банковский депозит с начислением по формуле сложных процентов (с капитализацией процентов). При таком способе накопления они в конце прогнозного периода приобретают форму капитала и измеряются в тех же единицах, что и остаточная стоимость объекта недвижимости. В таком виде обеспечивается реальный учет фактора времени, поскольку система банковского депозита деньги множит, а не обесценивает [8]. Таким образом, происходит капитализация текущих денежных доходов и превращение их в капитальную стоимость в конце расчетного периода. Для дисконтирования будущего капитала (суммы остаточной стоимости недвижимости и капитализированной стоимости денежных доходов) на дату оценки использовался коэффициент приведения (инфляции), рассчитанный за прогнозный период.
При использовании в качестве коэффициента приведения дисконтного множителя модель оценки стоимости объекта недвижимости методом НДД, в случае использования собственного капитала инвестора, будет иметь вид
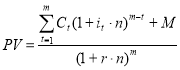 (11)
(11)
Где ![]() текущая стоимость оцениваемого объекта недвижимости;
текущая стоимость оцениваемого объекта недвижимости; ![]() наименование временного интервала прогнозного периода;
наименование временного интервала прогнозного периода; ![]() число временных интервалов в прогнозном периоде;
число временных интервалов в прогнозном периоде; ![]() чистый операционный доход
чистый операционный доход ![]() го временного интервала прогнозного периода, ден. ед. / временной интервал;
го временного интервала прогнозного периода, ден. ед. / временной интервал; ![]() процентная банковская ставка по вкладам (депозитам) для t — го временного интервала прогнозного периода, 1/ временной интервал;
процентная банковская ставка по вкладам (депозитам) для t — го временного интервала прогнозного периода, 1/ временной интервал; ![]() один заданный период дисконтирования денежных потоков, временной интервал;
один заданный период дисконтирования денежных потоков, временной интервал; ![]() ставка дисконтирования, 1/ временной интервал;
ставка дисконтирования, 1/ временной интервал; ![]() остаточная стоимость объекта недвижимости, ден. ед.
остаточная стоимость объекта недвижимости, ден. ед.
Параметр ![]() в формуле (11) может быть рассчитан из соотношения
в формуле (11) может быть рассчитан из соотношения ![]() .
.
В числителе формулы (11) текущие доходы в конце каждого расчетного интервала времени передаются на банковский депозит с начислением дохода по формуле сложных процентов, которые в конце прогнозного периода приобретают форму капитала и измеряются в тех же единицах, что и остаточная стоимость объекта недвижимости. Таким образом, происходит капитализация текущих денежных доходов и превращение их в капитальную стоимость в конце прогнозного периода. В знаменателе формулы (10) для приведения к дате оценки остаточной стоимости и капитализированных на конец прогнозного периода текущих денежных доходов используется коэффициент дисконтирования, основанный на сложном проценте.
Проиллюстрируем расчеты по формуле (11) на условном примере.
Дано: ![]() ; m=5;
; m=5; ![]() руб.;
руб.; ![]() руб.;
руб.; ![]() руб.;
руб.; ![]() руб.;
руб.; ![]() руб.;
руб.; ![]() 1 год;
1 год; ![]() ;
; ![]() ;
; ![]()
Ставка процента и ставка дисконтирования в течение прогнозного периода не изменяются.
Определить рыночную стоимость недвижимости.
- Рассчитаем будущую стоимость текущих денежных потоков:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- Рассчитаем общую сумму стоимости будущих денежных потоков и остаточной стоимости недвижимости в конце прогнозного периода:
![]()
- Рассчитаем значение дисконтного множителя:
![]() .
.
- Рассчитаем текущую стоимость недвижимости:
![]()
Для сравнения, полученного по формуле (11) результата оценки недвижимости, выполним по предыдущим исходным данным расчет рыночной стоимости недвижимости по формуле (1). Исходные данные и результаты расчета по формуле (1) приведены ниже в таблице.
|
Наименование параметра |
Значение параметра | ||||
|
|
1-й |
2-й |
3-й |
4-й |
5-й |
|
|
|
1200 |
1300 |
1400 |
1500 |
|
|
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
х |
х |
х |
х |
10000 |
|
|
|
1,2544 |
1,4049 |
1,5735 |
1,7623 |
|
|
892,9 |
956,6 |
925,3 |
889,7 |
851,2 |
|
|
892,9+956,6+925,3+889,7+851,2=4515,7 | ||||
|
|
5674,4 | ||||
|
|
4515,7+5674,4=10190,1 | ||||
Примечания: ![]() текущая стоимость реверсии;
текущая стоимость реверсии; ![]() текущая стоимость недвижимости.
текущая стоимость недвижимости.
Результаты оценки стоимости недвижимости, рассчитанные по формуле (1) и формуле (11), различаются незначительно (1,6 %), что связано с разницей в значениях ставки процента и ставки дисконтирования в формуле (11). Чаще всего процентные ставки приравниваются к ставкам по банковским вкладам на депозит, а ставки дисконтирования — к банковским ставкам по кредитам. Если значения ставок дисконтирования будут значительно выше значений процентных ставок, то результаты расчета по формуле (11) будут ниже результатов расчета по формуле (1). В этом случае при использовании для оценки стоимости недвижимости формулы (1) получим завышение результатов оценки.
В заключение следует отметить, что предлагаемые исправления недостатков формулы сложного процента и модели оценки стоимости недвижимости методом НДД являются корректными с точки зрения математики, содержит необходимые дополнительные параметры, имеет расшифровки всех параметров и их единиц измерения и примеры их практического использования.
Литература:
- Грибовский С. В. Методы капитализации доходов. Курс лекций. Санкт-Петербург, 1977. 172 с.
- Оценка недвижимости: Учебник / Под ред. А. Г. Грязновой, М. А. Федотовой. М.: Финансы и статистика, 2004. 496 с.
- Элементы финансовой математики для оценщиков (курс лекций и сборник задач). Составитель и ответственный редактор канд. физ.-мат. наук, зам. директора ПИНО Т. Г. Касьяненко. СПб., ЗАО «ПИНО», 1997. 64 с.
- Четыркин Е. М. Финансовая математика: Учебник. — 4-е изд. М: Дело, 2004. 400 с.
- Бадюков В. Ф. Финансовая математика: учеб. пособие / В. Ф. Бадюков, М. Ю. Серкин. Хабаровск: РИЦ ХГАЭП, 2009. 92 с.
- Мочулаев В. Е. Мнимые безразмерные показатели в теории оценки стоимости объектов гражданских прав / В. Е. Мочулаев // Вопросы оценки. 2014. № 4.
- Мочулаев В. Е. Методические проблемы реализации метода дисконтированных денежных потоков в оценке стоимости недвижимости // Вопросы оценки. 2011. № 3.
- Дасковский В. Об учете фактора времени при оценке эффективности инвестиционных проектов // Хранение и переработка сельхозсырья. 2003. № 3.

