Тема позиционирования затрагивается уже не в первый раз. Местоположение объекта может быть определено в терминах как глобальных, так и локальных координат. Без сомнений точность глобального позиционирования превосходит локальное. При использовании указанных систем, точность позиционирования составляет порядка 5–10 м в практически любой точке земного шара [1]. Но, к сожалению, не всегда применимо. Слабая сторона этого метода в том, что использование системы GPS недопустимо в здании из-за сильного погашения сигналов в стенах и перекрытиях зданий. Поэтому в большинстве мобильных приложение, ориентированных на определение местоположения объектов, применяются локальные методы геопозиционирования.
Идея использовать точки доступа Wi-Fi не нова и широко применяется для самых разных задач, наиболее передовыми в этой области являются сервисы skyhook, wi2geo, Google maps и Яндекс карты, Яндекс локатор. Эти сервисы предоставляют информацию о местоположении объекта в любой точке города с помощью зарегистрированных Wi-Fi сетей, используя различные методы. Однако, на практике точность этих координат, может достигать 140 метров и более, а при условии, что объект будет находиться вне города, где точек доступа малое количество, и вообще до 2 км. Эти цифры просто огромные, когда речь идет о ребенке, который живет в 100 метрах от школы. Для уменьшения погрешности многие разработчики используют различные технологии и комбинации алгоритмов.
В статье было рассмотрено несколько алгоритмов позиционирования, проведено сравнение нескольких по определенным критериям.
- Модулируемая ситуация.
Исследования проходят в модулируемом помещении (рис. 1), в котором расположены позиционируемые объекты, в дальнейшем просто объект. В качестве них выступают мобильные устройства, которые способны передавать Wi-Fi сигнал. Также в модели помещения присутствуют точки доступа, которые способны принимать Wi-Fi сигнал. Для упрощения вычислений мы будем рассматривать помещение как плоскую среду, в которой присутствуют помехи от стен.
На рис. 1 изображен пример расположения объекта и точек доступа на плоскости, где OPi — i-я точка доступа, (Xi, Yi) — декартовы координаты i-й точки доступа, Pi — мощность сигнала от i-й точки доступа, O — объект, (X0, Y0) — декартовы координаты объекта, N — количество точек доступа.
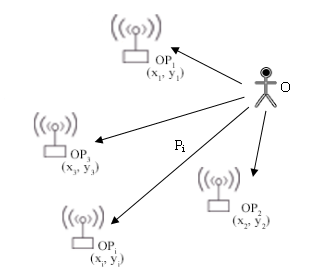
Рис. 1. Моделируемое помещение
- Критерии сравнения.
В каждом анализе должны присутствовать свои критерии оценки. Для данной работы были выбраны следующие критерии:
– Погрешность (это отклонение результата работы алгоритма от истинного положения объекта.);
– Вычислительная точность (зависимость количества вычислений, выполняемых алгоритмом, от размера входных данных);
- Алгоритмы позиционирования.
Для того, чтобы провести анализ необходимо ознакомиться с существующими алгоритмами. Ниже представлена краткая характеристика каждого.
Алгоритм 1. Наибольшая мощность.
Иногда такой алгоритм называют «Ближайшая точка доступа» [2]. Суть алгоритма присвоить объекту координаты той точки доступа, которая имеет сигнал наибольшей мощности. С точки зрения вычислений, это достаточно простой алгоритм. Например, если в помещении находятся несколько точек доступа (см. рис. 1) и одна из них (в данном случае OPi) имеет наибольшую мощность Pi, то местоположение объекта будет приравнено местоположению точки доступа OPi.
К достоинствам данного алгоритма относится простота реализации из-за низкой вычислительной сложности и необходимость знать только месторасположения точек доступа. Отрицательной стороной алгоритма является потеря точности определения, погрешность в помещении может достигать до 100 метров.
Алгоритм 2. Весовой алгоритм.
При использовании этого алгоритма координаты определяются как линейная комбинация координат точек доступа с учетом характеристики веса (т. е. мощность сигнала) [3]. Вычислительная сложность, так же как и в предыдущем, является простой. Координаты определяется по формулам:
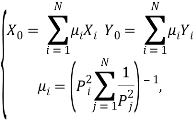(1)
где 
— характеристика веса.
К достоинствам данного алгоритма относится простота реализации из-за низкой вычислительной сложности и необходимость знать только месторасположения точек доступа. Недостатком является зависимость от числа точек доступа одновременно доступных объекту. У данного алгоритма по сравнению с предыдущим точность определения более высокая, однако, для наиболее точного позиционирования внутри помещений этих результатов мало.
Алгоритм 3. Геометрический подход (Триангуляция).
Определение координат точек методом триангуляции заключается в построении на местности системы смежных треугольников, вершинами которых являются определяемые и вспомогательные точки. При определении координат точек методом триангуляции проводятся вычислительные работы, которые включают:
– обработку полевых материалов и предварительные вычисления;
– вычисление координат точек, определенных засечками (прямой засечки);
– уравнивание триангуляции.
В данной работе вычисления засечки проводятся методом «по котангенсам углов треугольников». Так же существует второй метод «по котангенсам дирекционных углов направлений». При его использовании стоит учитывать, что значения дирекционных углов направлений находятся в пределах 5–85°, 95– 175о, 85–265°, 275–355°.
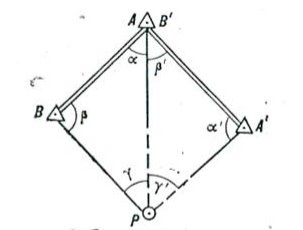
Рис. 2. К вычислению прямой засечки по котангенсам углов треугольников
Вычисление засечки по котангенсам углов треугольников выполняется по формулам:
,
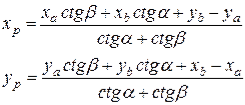где ха, yа, хb, yb — координаты точек доступа А и В;
хp, yp — координаты объекта Р;
αap, αbp — дирекционные углы направлений с точек доступа A и В на объект Р.
Проверка полученных координат производиться по следующей формуле:
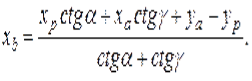
Достоинством данного алгоритма является его оперативность и достаточная высокая точность определения координат (при определенных условиях). Недостатком алгоритма является использование достаточно большого расхода памяти устройства для хранения необходимых переменных.
Алгоритм 4. Минимизация функционала (Дифференциальная латерация).
Координаты объекта вычисляются через минимизацию функционала, ядром которого является отношение затуханий сигнала от 1 и i-й точек доступа до произвольной точки с координатами (x,y).Будем считать, что коэффициент затухания сигнала, выраженный в децибелах, соответствует формуле:
(2)
где d — расстояние до агента, P0 — значение мощности сигнала на расстоянии одного метра и n — коэффициент распространения сигнала. Значения P0 и n неизвестны. Для того чтобы избавиться от этих неопределенных параметров, будем оценивать положение пользователя через минимизацию следующего функционала:
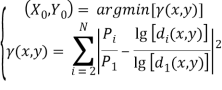(3)
где P1 и Pi — это мощность сигнала в децибелах принятая соответственно 1 и i-й точкой доступа, d1 и di — расстояния соответственно от 1 и i-й точки доступа до текущей точки с координатами (x,y).
Достоинствами являются простота реализации и достаточно высокая точность. К недостаткам можно отнести повышенную вычислительную сложность, так как применяется метод перебора (большое количество точек может значительно замедлить выполнение). Для повышения качества работы алгоритма необходимо начальное приближение, что позволит уменьшить вычислительную сложность. Алгоритм имеет различные модернизации.
Тестирование.
Для тестирования алгоритмов была смоделирована среда (рис. 6), представляющая собой квадратное помещение размером 50 × 50 м2. По углам помещения расположено четыре одинаковые точки доступа со следующими локальными координатами: OP1(0; 0), OP2(0; 50), OP3(50; 50) и OP4(50; 0) [2]. Работа алгоритма проверяется в следующих точках: O0(35; 25), O1(10; 10), O2(10; 40), O3(40; 40) и O4(40; 10).
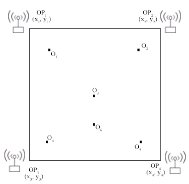
Рис. 3. Смоделирована среда
Мощность сигнала от каждой точки доступа в помещении изменяется согласно модели распространения радиоволн по формуле:
(4)
где 
— расстояние до объекта, 
— потеря мощности сигнала на расстоянии , 
— мощность передатчика, 
— мощность сигнала на приемнике на расстоянии , 
— расстояние 1 метр, 
— коэффициент распространения сигнала в среде.
Для вычисления мощности сигнала в работе были подобраны следующие параметры:
Погрешность вычисляется, как среднее арифметическое всех отклонений (разность между истинным значением и получившимся в ходе вычислений) разных точек:
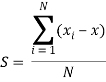
Таблица 1
Результаты тестирования
|
Алгоритм |
Погрешность (м) |
|
Наибольшая мощность |
20–25 м (количество точек доступа от 3–4) |
|
Весовой алгоритм |
15 м |
|
Геометрический подход (Триангуляция) |
8 м |
|
Минимизация функционала (Дифференциальная латерация) |
0–10 м (в зависимости от параметров среды, n) |
Заключение.
Из результатов тестирования (см. таблицу 1) видно, что те алгоритмы, где сложность вычислений больше показывают наибольшую точность. Обратим внимание на первые два алгоритма. В них на точность влияет количество точек доступа. Чем их больше, тем и погрешность вычислений меньше. Это происходит из-за того, что не проводиться предварительной подготовки к определению координат объектов. В последних двух, погрешность зависит от подготовки моделируемой среды. Например, при минимизации функционала, погрешность почти исчезает при хорошо подобранных параметров. Однако в реальных условиях подбор данного параметра является весьма трудоемкой задачей, ввиду географии среды и возникающих помех.
В статье рассмотрено несколько алгоритмов локального позиционирования при использовании точек доступа Wi-Fi и вышек сотовых операторов.
Исходя из данных в табл. 1 и описания алгоритмов можно сделать вывод, что точность определения зависит от количества вычислений проводимых в ходе выполнения. Можно увидеть обратно пропорциональную зависимость. Чем сложнее вычисления, тем погрешность меньше. Но, с другой стороны, алгоритмы с более сложной вычислительной структурой являются более трудоемкими на подготовительном этапе.
При написании программ на мобильные устройства стоит сокращать использование таких характеристик, как память и вычислительные ресурсы, следовательно, для достижения оптимальных результатов следует использовать комбинированные алгоритмы (т. е. алгоритмы, совмещающие в себе два и более), позволяющие использовать приемлемое количество памяти при невысокой вычислительной сложности. Комбинирование позволит значительно сократить средства, затраченные на подготовку, и уменьшить погрешность определения местоположения объекта.
В ходе анализа можно сказать, что наиболее сбалансированный алгоритм является триангуляция, которая хоть и имеет погрешность, а также неэкономично использует память устройств, но в сравнении с другими алгоритмами за счет использования дополнительного оборудования приводит к балансу затраченных средств и погрешности.
Литература:
- Аверин И. М., Семенов В. Ю. Позиционирование пользователей с использованием инфраструктуры локальных беспроводных сетей. IV Всероссийская конференция “Радиолокация и радиосвязь”. ИРЭ РАН. 29 ноября — 3 декабря 2010 г.
- Миниахметов Р. М., Рогов А. А., Цымблер М. Л. Обзор алгоритмов локального позиционирования для мобильных устройств. Вестник ЮУрГУ. Серия “Вычислительная математика и информатика”. Т. 2. № 2. 2013.
