«Бизнес для бизнеса» («B2B») — вид информационного и экономического взаимодействия, где в качестве субъектов выступают юридические лица (далее компании), целью которого является не работа на конечного потребителя, а на такие же компании, т. е. на другой бизнес. Математический аппарат теории игр позволяет сосредоточиться на выборе стратегий, которые компании могут использовать для увеличения своей прибыли и адекватной реакции на действия своих оппонентов по рынку, анализу равновесных ситуаций на рынке и в целом выбора модели своего поведения. Различные расширения позволяют моделировать ситуации в условиях неопределенностей, такие как сигнальные игры и равновесие Байеса.
Исследование теоретико-игровых моделей дуополий в условиях различных неопределенностей является достаточно популярной темой, большой вклад в неё сделали [1] и [2], показавшие, что в условиях дуополии Курно когда предельные издержки производства игроков являются приватной информацией и для оппонентов представляются случайными величинами, прибыльнее делиться приватной информацией о них. В [3] этот подход был расширен и дополнен, позволяя уточнить условия, при которых компании в условиях схожих неопределенностей смогут увеличить свою прибыль, при этом не только в рамках олигополии Курно, но также и Бертрана.
Модель [4] приводит сигнальный механизм обмена информации между игроками и позволяет оценить его выгодность в зависимости от качества сигнала, уточняющего спрос, получаемого игроками.
Модели, приведенные в [3] и [4] связывает общая идея: насколько выгодно игроку (т. е. компании) раскрыть собственную приватную информацию, при этом получить доступ к информации о некоем сегменте рынка (участниках информационного обмена на некоей онлайновой площадке с открытой историей транзакций, позволяющей уточнить параметры, являющиеся неопределенными для других игроков).
Остановимся на рассмотрении и сравнении результатов, представленных в данных моделях. В рамках модели [4], в дуополии Курно, игроки получают приватные сигналы об одном из неопределенных параметров линейной функции спроса (коэффициенты сдвига и углового наклона), и далее рассматривается две ситуации: когда они делятся информацией, и когда не делятся. Сигналы в обоих случаях могут быть как информативными, так и не информативными. Авторами модели была получена квадратичная зависимость между уровнем информативности сигнала (трактуемого как уровень неопределенности, с которым сталкиваются участники рынка) и объемом прибыли, получаемого игроками.
В рамках модели [3] получена аналогичная зависимость между уровнем неопределенности (параметрами распределения вектора случайных величин, задающего издержки, и соответствующего ему ковариационной матрицы), для олигополий Курно и Бертрана. Однако стоит заметить, что в случае олигополии Бертрана, в отличие от предыдущих моделей, товары не идентичны, а дифференцируемы, и это также повлияет на уровень прибыли. Далее представлены результаты компьютерного моделирования, проведенного на основании математического аппарата, изложенного в данных моделях.
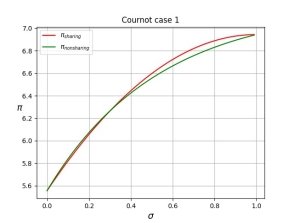
Рис. 1. Результат моделирования [3] в случае неопределенного первого параметра
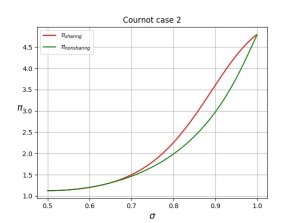
Рис. 2. Результат моделирования [3] в случае неопределенного второго параметра
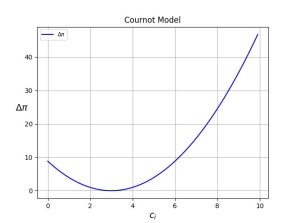
Рис. 3. Результат моделирования [4] в случае олигополии Курно
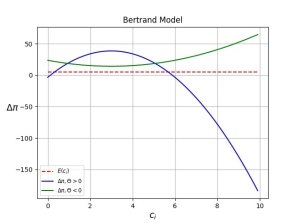
Рис. 4. Результат моделирования [4] в случае олигополии Бертрана с дифференцируемыми товарами
На рисунках 1 и 2 представлены результаты моделирования для модели [3], где 
и 
обозначают прибыли игроков в условиях равновесия в случае когда они делятся информацией и не делятся соответственно. Уровень информативности сигнала обозначен как 
. Нетрудно заметить, что прибыль в случае, когда игроки делятся информацией, начинает превышать прибыль для случая, когда игроки не делятся информацией, начиная с определенного значения уровня информативности сигнала, в данном случае это 
и 
соответственно.
На рисунках 3 и 4 представлены результаты моделирования для модели [4], где 
обозначает разность между прибылью в случае дележа и не дележа информацией для конкретного игрока с уровнем издержек 
, позволяя оценить, насколько выгодно ему будет вступать в информационный обмен. На рисунке 4 так же показано, как меняется прибыль в зависимости от уровня дифференцированности товаров 
.
К сожалению, в силу структурных различий обеих моделей невозможно корректно напрямую сравнить их результаты, однако можно сделать достаточно контр-интуитивный вывод: делиться информацией о себе бывает достаточно выгодно. Насколько же это выгодно? Зависит от модели поведения игроков на рынке и уровня неопределенности, с которым они могут столкнуться при осуществлении хозяйственной деятельности. Теоретико-игровые модели в большинстве своём являются иллюстративными, предоставляя лишь информацию о природе стратегических решений, принимаемых участниками рынка.
Литература:
- Gal-Or, R. Information sharing in oligopoly // Econometrica, 1985. Vol.53, No. 2. P. 329–343.
- Shapiro, C. Exchange of cost information in oligopoly // Review of Economic Studies, 1986. Vol. 53, No. 3. P. 433–446.
- Zhu, K. Information transparency of business-to-business electronic markets: A game-theoretic analysis // Management Science, 2004. Vol. 50, No. 5. P. 670–685.
- Lopez Rodrıguez, J. Information exchanges in Cournot duopolies // RBE Rio de Janeiro, 2003. Vol. 57, No.1. P. 191–208.
