Проблемы существования и нахождения значения и ситуаций ε-равновесия для общей марковской игры решены путем аппроксимации ее марковской игрой с переоценкой (дисконтированием). В качестве примера рассмотрена марковская игра «Большой матч».
- Марковская игра спереоценкой. Марковскую игру можно задать с помощью множества прямоугольных матриц (игр компонент) Г = {Г1, Г2, …, ГN} (см. [1]):
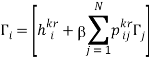 ,
,
где Гi(i= 1, 2, …, N) ̶ состояние игры,k (r) ̶ решение игрока I (II), принимаемое в i-м состоянии; kAi = {1, 2, …, ki}, rBi = {1, 2, …, ri}; [0, 1) ̶ коэффициент переоценки (дисконтирующий множитель).
Процесс игры определяется следующим образом. Пусть на очередном шаге разыгрывается игра-компонента Гi (игра находится в состоянии i). Игрок I и II независимо выбирают строку k и столбец r соответственно. В результате игрок II платит игроку I ![]() единиц, и согласно распределению
единиц, и согласно распределению ![]() определяется следующее состояние Гj. После чего игра продолжается по той же схеме. Выигрыши на протяжении игры накапливаются. Игрок I стремится максимизировать свой накопленный выигрыш, в то время как игрок II стремится его минимизировать. Суть коэффициента переоценки состоит в том, что единица выигрыша игрока I через n шагов игры будет стоить nединиц.
определяется следующее состояние Гj. После чего игра продолжается по той же схеме. Выигрыши на протяжении игры накапливаются. Игрок I стремится максимизировать свой накопленный выигрыш, в то время как игрок II стремится его минимизировать. Суть коэффициента переоценки состоит в том, что единица выигрыша игрока I через n шагов игры будет стоить nединиц.
Обозначим: ![]() ̶ вероятность выбора решения kAiигроком I в состоянии i на n-м шаге игры;
̶ вероятность выбора решения kAiигроком I в состоянии i на n-м шаге игры; ![]() ̶ вероятность выбора решения rBiигроком II в состоянии i на n-м шаге игры;
̶ вероятность выбора решения rBiигроком II в состоянии i на n-м шаге игры; ![]() ;
; ![]() ; S = {1, 2, …, N}.
; S = {1, 2, …, N}.
Решающей функцией на n-м шаге игрока I называется набор распределений xn = {Xi(n), 1≤i≤N}, а игрока II ̶ yn= {Yi(n), 1≤i≤N}. Стратегией игрока I называется последовательность решающих функций π = (x1, x2, …, xn, …), а игрока II ̶ φ= (y1, y2, …, yn, …). Стратегии вида x = (x, x, …, x, …), y = (y, y, …, y, …) называются стационарными. Множества стратегий игроков обозначим: = {π}, = {φ}, X= {x}, Y= {y}. В дальнейшем при рассмотрении стационарных стратегий, верхний индекс будет опущен. Множество ΣS = XY называется классом стационарных стратегий, множество ΣM= классом марковских стратегий.
На n-м шаге игры при заданных стратегиях π и φ вероятность перехода из состояния iSв состояние jSравна
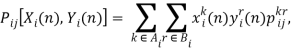
а ожидаемый выигрыш игрока I равна

При любых нестационарных стратегиях π и φ игроков рассматриваемый процесс является, вообще говоря, неоднородной цепью Маркова, для которой матрица вероятностей перехода за n шагов имеет вид
![]()
где P(xn, yn) является матрицей перехода размера N×N, (i, j)-й элемент которого равен
![]() . При n = 0 положим P0(π, φ) = I(единичная матрица размера N×N). Решающим функциям xn и yn соответствует (N×1)-мерный вектор выигрышей H(xn, yn) = {
. При n = 0 положим P0(π, φ) = I(единичная матрица размера N×N). Решающим функциям xn и yn соответствует (N×1)-мерный вектор выигрышей H(xn, yn) = {![]() }.
}.
Эти обозначения позволяют представить функцию выигрыша марковской игры с переоценкой и конечным числом шагов Т как N-мерный вектор-столбец
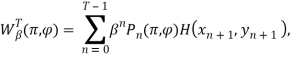
i-й элемент которого отвечает i-му начальному состоянию игры.
Тройка Γ = , , ![]() называется марковской игрой с переоценкой и конечным числом шагов. Подыгра = X, Y,
называется марковской игрой с переоценкой и конечным числом шагов. Подыгра = X, Y, ![]() игры Γ называется марковской игрой с переоценкой и конечным числом шагов в стационарном режиме. Верхнее и нижнее значения игры Γ определяются следующими N-мерными вектор столбцами:
игры Γ называется марковской игрой с переоценкой и конечным числом шагов в стационарном режиме. Верхнее и нижнее значения игры Γ определяются следующими N-мерными вектор столбцами:
![]() ,
, ![]()
Таким же образом определяются верхнее ![]() и нижнее
и нижнее ![]() значения игры . Игра Γ () имеет значение v(Γ) (v()), если ее верхнее и нижнее значения равны.
значения игры . Игра Γ () имеет значение v(Γ) (v()), если ее верхнее и нижнее значения равны.
Из принципа оптимальности Беллмана и принципа максимина фон Неймана вытекает существование значение игры Γ. Значение ![]() (iS)игрыΓ и оптимальные стратегии π*и φ*игроков могут быть определены с помощь функционального уравнения преобразования цен:
(iS)игрыΓ и оптимальные стратегии π*и φ*игроков могут быть определены с помощь функционального уравнения преобразования цен:
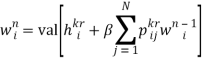 , iS, n= 1, 2, …, T, (1)
, iS, n= 1, 2, …, T, (1)
где ![]() jS;
jS; ![]() ̶ i-я компонента вектора
̶ i-я компонента вектора ![]() ; val [] ̶ значение (цена) игры с матрицей [].
; val [] ̶ значение (цена) игры с матрицей [].
Марковская игра с переоценкой и бесконечным числом шагов ΓW = , , ![]() исследована в [2] с помощью операторов сжатия.
исследована в [2] с помощью операторов сжатия.
- Общая марковская игра. Постановка задачи. Когда число шагов бесконечно в качестве функции выигрыша может быть рассмотрен предельный средний выигрыш игрока I
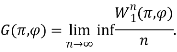
Общая марковская игра, задаваемая тройкой ΓG = , , G(π, φ), характеризуется тем, что при любых стационарных стратегиях игроков множество состояний игры S разбивается на несколько эргодических множеств и невозвратное множество, которые могут меняться в зависимости от стратегий игроков. Такая игра изучена в работах [3, 4].
Наша цель ̶ исследовать проблемы существования и нахождения значения и ситуаций ε-равновесия для общей марковской игры путем аппроксимации ее марковской игрой с переоценкой.
-
Существование инахождение значения иситуаций ε-равновесия для общей марковской игры.Напомним, что если P — стохастическая матрица, то последовательность {Pn} суммируема по Чезаро к некоторой стохастической матрице P*. Отсюда следует суммируемость по Абелю последовательности {Pn} к матрице P*, то есть
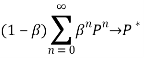 при 1 ̶ 0.
при 1 ̶ 0.
Пусть
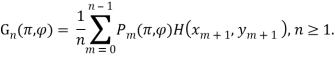
Обозначим ![]() .
.
Лемма 1. В классе стационарных стратегий ΣS сходимость ![]() равномерна.
равномерна.
Данное утверждение является следствием теоремы 6.3 из [3, 4].
Лемма 2. В классе стационарных стратегий ΣS сходимость
Доказательство. Согласно доказательству теоремы Фробениуса (см. [5]) имеем
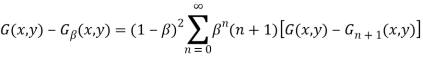 .
.
Сумму справа разобьем на две:
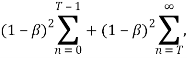
причем, ввиду леммы 1, для любого заданного числа ε>0 существует такой не зависящий от (x, y)ΣS номер Т, что при n>T норма ![]() для всех (x, y)ΣS. Тогда вторая сумма по норме будет меньше ε вне зависимости от , а для первой суммы того же можно добиться за счет приближения к 1 (независимо x от и y). Таким образом, по заданному ε>0 найдется не зависящей от (x, y)ΣS значение ε(0, 1) такое, что при > ε будет
для всех (x, y)ΣS. Тогда вторая сумма по норме будет меньше ε вне зависимости от , а для первой суммы того же можно добиться за счет приближения к 1 (независимо x от и y). Таким образом, по заданному ε>0 найдется не зависящей от (x, y)ΣS значение ε(0, 1) такое, что при > ε будет ![]() для всех (x, y)ΣS. Лемма доказана.
для всех (x, y)ΣS. Лемма доказана.
Теорема 1. Пусть множества S, Aiи Bi(iS) конечны. Тогда общая марковская игра в стационарном режиме G = , , G(x, y) имеет значение, т. е.
![]()
Доказательство. Существование значения игры G будет доказано, если покажем существование ситуации ε-равновесия (xε, yε) в классе стационарных стратегий ΣS.
Последовательность {Pn(x, y)} суммируема по Чезаро к P*(x, y). Отсюда следует суммируемость по Абелю последовательности{Pn(x, y)} к P*(x, y). Следовательно,![]() . Отсюда и из леммы 2 следует, что для любого ε>0 при достаточно близости коэффициента переоценки к 1 имеет место двойное неравенство
. Отсюда и из леммы 2 следует, что для любого ε>0 при достаточно близости коэффициента переоценки к 1 имеет место двойное неравенство
![]() (2)
(2)
где 1N-мерный вектор столбец с компонентами, равными 1.
С другой стороны, для марковской игры с переоценкой в классе стационарных стратегий ΣS существует ситуация ε-равновесия, ибо в ΣS при любом (0, 1) данная игра имеет значение [2]. Откуда для любого ε>0 справедливы неравенства
![]()
Отсюда и из (2) следует, что
![]()
Здесь вновь используя неравенства (2), имеем
![]()
Это значит, что для общей марковской игры в классе ΣS существует ситуация ε-равновесия (xε, yε) и, следовательно, данная игра в классе ΣS имеет значение. Теорема доказана.
Обобщим этот результат.
Теорема 1. Пусть множества S, Aiи Bi(iS) конечны. Тогда общая марковская игра ΓG = , , G(π, φ) имеет значение, а оба игрока ε-оптимальные стационарные стратегии, т. е.
![]()
Доказательство. Определим
![]()
Аналогично для фиксированной стратегии xXигрока I:
![]()
Учитывая, что в рассматриваемой игре знаки sup (inf) и max (min) равнозначны, имеем
![]()
![]()
![]() (3)
(3)
Поскольку ![]() , все неравенства (3) на самом деле являются равенствами, что и доказывает теорему.
, все неравенства (3) на самом деле являются равенствами, что и доказывает теорему.
Согласно доказательству теоремы 1 при достаточной близости коэффициента к 1 ситуация равновесия (x*, y*)ΣS игры с переоценкой ΓG = , , G(π, φ) является ситуацией ε-равновесия общей марковской игры ΓG. Для марковской игры с переоценкой с бесконечным числом шагов ΓW = , , ![]() имеет место функциональное уравнение преобразования цен [2]
имеет место функциональное уравнение преобразования цен [2]
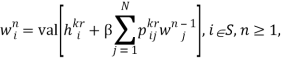
где
Умножим обе части исходного равенства на 1 и в полученном соотношении положим ![]() . В результате имеем
. В результате имеем
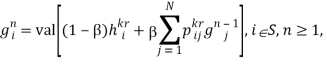 (4)
(4)
где ![]() , iS.
, iS.
Последовательность векторов ![]() при n сходится к значению игры с переоценкой в стационарном режиме
при n сходится к значению игры с переоценкой в стационарном режиме ![]() . Оптимальные стационарные стратегии игроков x* и y* определяются путем решения матричных игр
. Оптимальные стационарные стратегии игроков x* и y* определяются путем решения матричных игр
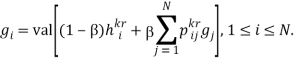 (5)
(5)
Для заданного ε>0 значение общей марковской игры ΓG определяется с помощью рекуррентного соотношения (4), постепенно приближая коэффициента к 1.
4. Пример. Марковская игра «Большой матч». Полученные результаты применим к игре «Большой матч», задаваемой тремя игр-компонентами [3, 4, 7–9]:
![]()
Применение функционального уравнения (5) к играм-компонентам Γ1, Γ2, Γ3 дает
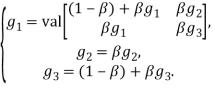 (6)
(6)
Из 2-го и 3-го уравнения получаем
![]()
Решая эту 22-игру (см. [9, c. 45]), находим значение данной игры ΓG и оптимальные стратегии игроков
![]()
Отсюда можем определить значение игры «Большой матч»
![]()
и ε-оптимальные стратегии игроков
![]()
где ![]() .
.
Заметим, что игрок I кроме ε-оптимальной стратегии xε имеет также оптимальную стратегию ![]() В то же время игрок II имеет лишь ε-оптимальную стратегию yε, так как
В то же время игрок II имеет лишь ε-оптимальную стратегию yε, так как ![]() не оптимальна, ибо
не оптимальна, ибо ![]() при стратегии x' = (1, 0) игрока II.
при стратегии x' = (1, 0) игрока II.
Литература:
- ЛьюсР. Д., РайфаХ. Игрыирешения. Введениеикритическийобзор. М.: Изд. иностр. литературы, 1961. 642 с.
- ИбрагимовА. А. Осуществованиииединственностиситуацииравновесиявмарковскихиграхспереоценкой // НАНУкраины. Кибернетикаисистемныйанализ. 2000. № 6. С. 152–165.
- ИбрагимовА. А. Марковскиеигрыснесколькимиэргодическимиклассами // Украинскийматематическийжурнал. 2003. Т 55. № 6. С. 466–471.
- ИбрагимовА. А. Существованиезначениявобщихмарковскихиграх // ИзвестияРАН. Теориясистемыуправления. 2004. № 2. С. 5–15.
- ФихтенгольцГ. М. Курсдифференциальногоиинтегральногоисчисления. Том 2. М.: Наука. 800 с.
- МайнХ., ОсакиС. Марковскиепроцессыпринятиярешений. М.: Наука, 1977. 176 с.
- ИбрагимовА. А. Омарковскойигре«большойматч» // РАН. Автоматикаителемеханика. 2000. № 11. С. 104–113.
- ИбрагимовА. А. Марковскаяигра«Большойматч»вклассестационарныхстратегий // Журнал«Молодойученый»№ 4 (84), март, 2015 г. Москва. С. 4–7.
- ДюбинГ. Н., СуздальВ. Г. Введениевприкладнуютеориюигр. М.: Наука, 1981. 336 с.







