Покрытием множества 
называется такое семейство 
его подмножеств, что 
. В случае когда 
— топологическое пространство, это покрытие называется открытым (замкнутым) покрытием пространства 
, если все множества 
открыты (замкнуты).
Определение 1. Топологическое пространство называется компактным, если из всякого его открытого покрытия можно выделить конечное подпокрытие.
Хаусдорфовы компактные пространства называется компактами.
Определение 2. Точка 
называется предельной точкой множества 
, если во всякой окрестности точки 
содержится бесконечно много точек множества 
. Точка называется точкой полного накопления множества , если для всякой ее окрестности 
множества 
и 
равномощны.
Определение 3. Топологическое пространство называется счетно-компактным, если из всякого его счетного открытого покрытия можно выделить конечное подпокрытие.
Теорема 1. Топологическое 
-пространство счетно-компактно тогда и только тогда, когда всякое бесконечное подмножество имеет предельную точку.
Доказательство. Необходимость. Предположим противное, что в существует бесконечное подмножество, 
которое не имеет предельных точек. Известно, что -пространстве всякое множество без предельных точек замкнуто. Поэтому множество 
открыто. Поскольку множество 
замкнуто и не имеет предельных точек, у всякой точки 
существует окрестность 
, пересекающаяся с множеством 
в единственной точке 
. Из счетного покрытия 
можно выделить конечное подпокрытие 
. Тогда множество 
состоит из 
точек 
. Получили противоречие, что 
содержит бесконечное много точек.
Достаточность. Предположим противное. Существует счетное открытое покрытие 
пространства 
, из которого нельзя выделить конечного покрытия. Можно считать, что 
для всякого 
. Из каждой разностей 
выберем по точке 
и положим 
. Пусть 
— произвольная точка пространства 
. Тогда точка 
лежит в некотором элементе 
покрытия 
. Множество 
является окрестностью точки 
, пересекающейся с множеством 
не более чем по 
точке 
. Таким образом, бесконечное множество 
не имеет предельных точек. Получили противоречие. Теорема 6.1 доказана.
Определение 4. Топологическое пространство называется финально компактным, если из всякого его открытого покрытия можно выделить счетное подпокрытие.
Пример 1. Пусть
— числовая прямая с обычной топологией является финально-компактным, но не является компактным пространством.
Утверждение 1. В финально-компактным пространстве 
всякое несчетное множество регулярной мощности имеет точку полного накопления.
Доказательство. Предположим противное, что существует множество 
несчетной регулярной мощности 
, не имеющее точек полного накопления. Тогда у всякой точки 
существует окрестность 
, пересекающаяся с множеством 
по множеству мощности 
. Из покрытия 
пространства 
можно выбрать счетное подпокрытие 
. Следовательно, множество 
можно представить в виде счетной суммы множеств 
мощности 
, что противоречит регулярности и несчетности 
. Утверждение 1 доказано.
Теорема 2. Топологическое пространство 
компактно тогда и только тогда, когда всякое его бесконечное подмножество имеет точку полного накопления.
Доказательство. Необходимость. Пусть 
— компактное пространство. Тогда в силу замечания 1 пространство 
является финально компактным пространством. В силу утверждения 1 всякое бесконечное подмножество пространство 
имеет полного накопления.
Достаточность. Пусть бесконечное подмножество 
пространство имеет точку полного накопления 
, т. е. для каждой окрестности точки 
множества и равномощны. Это означает, что точка 
есть предельная точка множества 
. Покажем, что есть компактное пространство. Теорема 3. Пусть 
— тихоновское пространство. Тогда
.
Литература:
- Radul T. N. On the funtor of order-preserving functionals.//Comment.Math.Unif.Carol. 1998.V,39.No.3.P.609–615.
-
Жиемуратов Р. Е. Топологические и категорные свойства пространства нелинейных
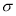-гладких функционалов. Канд. Дисс. Ташкент, ИМИТ, 2010, стр.69.
- Бешимов Р. Б. О слабой плотности топологических пространств // ДАН РУз. — 2000.– № 11. — С. 10–13.
