Цель работы — научиться составлять оптимальный план для транспортных средств на производстве с учетом ограничений, используя материальные запасы для транспортной задачи, получив оптимизацию планов математическими компьютерными методами линейного программирования посредством применения Solver из программы Microsoft Excel [1].
План транспортных средств представляется в табличной форме, включая количество производственных запасов на складах поставщиков и необходимое количество для потребителя в естественном выражении. При разработке плана производственная цель определена: минимизация расходов транспортировки [2].
Математическая модель для алгоритма оптимизации
Общее утверждение транспортной проблемы включает определение оптимального плана транспортных средств некоторого груза от ![]() пунктов отправления
пунктов отправления ![]() до
до ![]() мест назначения
мест назначения ![]() . Как критерий оптимальности мы берем или минимальную стоимость транспортных средств всего груза, или минимальное время его поставки [3].
. Как критерий оптимальности мы берем или минимальную стоимость транспортных средств всего груза, или минимальное время его поставки [3].
Пусть ![]() (
(![]() ) — тарифы транспортировки единицы груза от
) — тарифы транспортировки единицы груза от ![]() пункта отправления до
пункта отправления до ![]() места назначения;
места назначения; ![]() (
(![]() ) — груз
) — груз ![]() пункта;
пункта; ![]() (
(![]() ) — требование для груза в
) — требование для груза в![]() месте назначения;
месте назначения; ![]() (
(![]() ) — количество единиц груза, транспортируемых от
) — количество единиц груза, транспортируемых от ![]() пункта отправления до
пункта отправления до ![]() места назначения. Тогда экономико-математическая постановка задачи заключается в определении минимального значения функции:
места назначения. Тогда экономико-математическая постановка задачи заключается в определении минимального значения функции:
![]() (1)
(1)
с условиями
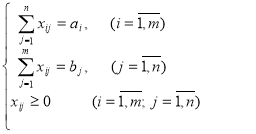 (2)
(2)
Если потребности в грузовых пунктах назначения равны грузовым резервам в пунктах отправления, т. е.
![]() (3)
(3)
тогда модель транспортной задачи называют закрытой, иначе — открытая.
Постановка задачи
Однородный груз в количестве 50, 30 и 10 единиц поступил на три базы ![]() . Этот груз требуется доставить в четыре места назначения
. Этот груз требуется доставить в четыре места назначения ![]() соответственно в количествах 30, 20, 10 и 20 единиц. Тарифы транспортных средств единицы груза даны в таблице 1. Найти оптимальный план транспортных средств транспортной задачи.
соответственно в количествах 30, 20, 10 и 20 единиц. Тарифы транспортных средств единицы груза даны в таблице 1. Найти оптимальный план транспортных средств транспортной задачи.
Табличная модель
Оформим план в форме таблицы:
Таблица 1
Транспортные тарифы
|
A |
B |
C |
D |
E |
F | |
|
1 |
Транспортная задача (minimum) | |||||
|
2 |
Поставщики |
Потребители |
Запас | |||
|
3 |
|
|
|
| ||
|
4 |
|
1 |
2 |
4 |
1 |
50 |
|
5 |
|
2 |
3 |
1 |
5 |
30 |
|
6 |
|
3 |
2 |
4 |
4 |
10 |
|
7 |
Потребность |
30 |
20 |
10 |
20 | |
После того, чтобы получить таблицу плана, необходимо составить формулы для вычислений (таблицы 2 и 3).
Таблица 2
Представление формул ивходных данных
|
… |
A |
B |
C |
D |
|
8 | ||||
|
9 |
|
|
| |
|
10 |
| |||
|
11 |
| |||
|
12 |
| |||
|
13 |
Импортировано |
=SUM(B10:B12) |
=SUM(С10:С12) |
=SUM(D10:D12) |
Таблица 3
Продолжение таблицы 2
|
E |
F |
G |
|
|
Экспортировано |
Остатки |
|
= SUM (B10:E10) |
| |
|
= SUM (B11:E11) |
| |
|
= SUM (B12:E12) |
| |
|
= SUM (E10:E12) |
На первых уроках нецелесообразно автоматизировать работу для планирования экспериментов и обработки результатов, поскольку студент получает готовые результаты, не показав действий, творчества. После ручного контроля эксперимента, когда понимание и знание объекта исследования улучшились, возможно начать автоматизацию планирования и управление экспериментом: изменяя число доставок в ячейках ![]() , сокращая расходы в ячейке
, сокращая расходы в ячейке ![]() . В то же время визуально управлять расходом запасов в колонке
. В то же время визуально управлять расходом запасов в колонке ![]() . Расход не должен превышать резервы на складе (колонка
. Расход не должен превышать резервы на складе (колонка ![]() ).
).
Посредством программы оптимизации мы можем облегчить реализацию этой задачи. После выбора Поиск Решения в MSExsell появится диалоговое окно, в котором мы установим следующие условия, показанные на рисунке 1:
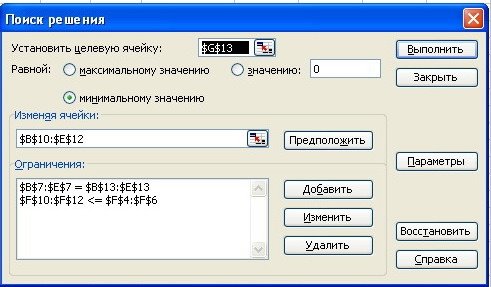
Рис. 1. Диалоговое окно Поиск решения
Мы принимаем модель как линейную, Рисунок 2:
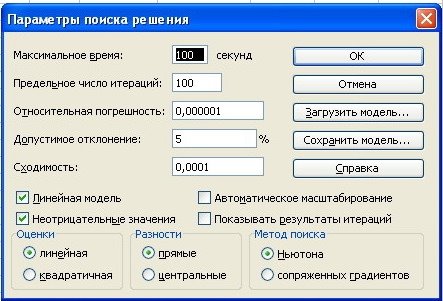
Рис. 2. Диалоговое окно «Параметры Поиска решения»
После нажатия на кнопку «Выполнить», получаем результат, приведенный в таблице 4.
Таблица 4
Полученные результаты
|
A |
B |
C |
D |
F |
G | ||
|
8 | |||||||
|
9 |
|
|
|
|
Экспортировано |
Остатки | |
|
10 |
|
20 |
10 |
0 |
20 |
50 |
0 |
|
11 |
|
10 |
0 |
10 |
0 |
20 |
10 |
|
12 |
|
0 |
10 |
0 |
0 |
10 |
0 |
|
13 |
Импортировано |
30 |
20 |
10 |
20 |
Об затраты |
110 |
Таким образом, достигнуты минимальные расходы при ограничениях запасов на складах поставщиков. Упростить и ускорить поиск прибыли помогла программа Solver, которая рационализировала решение этой экономической задачи [4].
Литература:
- Горчаков A. A. Компьютерные экономико-математические модели. M.: ЮНИТИ, 1995. — 201 с.
- Додж M. Эффективная работа с MicrosoftExcel 2000. SPb.: Питер, 2001. — 161 с.
- Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике. — M.: Изд. «ДИС», 2001. — 368 с.
- Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе. Изд. Юнити, 2001. — 367 с.
- Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. — 432 с.

