Определение толщины защитных покрытий

Представлены постановка и решение краевой задачи нестационарного теплопереноса применительно к двухслойной системе: полимерное покрытие — металлическое основание. Определены расчетные выражения для определения толщины покрытия. Разработаны метод теплового неразрушающего контроля и измерительная система, реализующая данный метод. Экспериментально получено подтверждение работоспособности метода.

Ключевые слова: двухслойное изделие, защитное покрытие, измерительная система, краевая задача, математическая модель, металлическое основание, неразрушающий контроль, полимерное покрытие, тепловой метод, теплопроводность, толщина.

Presented formulation and solution of the problem of unsteady heat transfer with respect to the two-layer system: polymeric coating — metal base. Defined calculation expressions to determine the thickness of the coating. We developed a method of thermal nondestructive testing and measuring system that implements this method. Experimentally obtained validation of the method.

Key words:two-layer product, the protective coating, the measuring system, the boundary value problem, the mathematical model, metal base, nondestructive testing, polymer coating, thermal method, the thermal conductivity, thickness.

Обозначения и аббревиатуры

Т — температура, С;

τ — время, c;

q — плотность теплового потока, Вт/м²;

h –линейный размер, м;

λ _— теплопроводность, Вт/(мК);

Fo — безразмерное время (число Фурье);

– безразмерная координата;

– температура в безразмерном представлении;

b₀, b₁ — параметры модели;

x, y,r — координаты, м;

R — радиус нагревателя, м;

В — константа прибора;

δ — относительная погрешность, %.

ТФС — теплофизические свойства;

ИС — измерительная система;

ИЗ — измерительный зонд;

ТП — термоэлектрический преобразователь;

БП — блок питания;

Н — нагреватель;

ПТФЭ — политетрафторэтилен.

Индексы

1 — первый слой;

2 — второй слой;

Для расчета многослойных композиционных материалов с заданными свойствами наилучшим образом подходят аналитические решения, так как они в явном виде содержат основные физические свойства среды. Получение решений задач теплопроводности для многослойных тел с помощью точных аналитических методов представляет большие математические трудности, так как появляется необходимость решения многопараметрических трансцендентных уравнений [1].

В последнее время все большее применение в теории теплообмена получают приближенные аналитические методы, а также совместное использование точных (Фурье, интегральных преобразований и др.) и приближенных (вариационных, взвешенных невязок, наименьших квадратов, коллокаций и др.) аналитических методов. Приближенные аналитические методы менее универсальны и более сложны, чем численные. Однако они обладают тем определенным преимуществом, что позволяют получать решения, хотя и приближенные, но в аналитической форме. Вследствие максимальной простоты этих решений они наиболее приспособлены для использования их в инженерной практике [2].

В данной работе применён подход, основанный на применении регулярных режимов, с целью получения аналитического решения для реализации неразрушающего метода определения толщины защитных покрытий на металлических основаниях [2–5].

В методе неразрушающего теплового контроля изделий использован круглый плоский источник тепла, расположенный на поверхности полуограниченного в тепловом отношении объекта [6–8]. Учтено, что регулярные тепловые режимы первого и второго рода имеют общее свойство, характеризующееся независимостью от времени отношения теплового потока в любой точке тела к потоку тепла на его поверхности. Данное свойство доказано Лыковым А. В. [6]. Математическая модель, описывающая термограмму, в данном случае чаще всего является линейной по параметрам или легко линеаризуется. Однако основная часть этих методов базируется на моделях для тех конечных размеров. Применительно же к методам НК следует говорить не о регулярном тепловом режиме для всего тела (так как оно принимается неограниченным), а о регуляризации теплового процесса только для определенной (локальной) области тела. Можно проводить термический анализ, основываясь только на участке термограммы, соответствующем регуляризации теплового режима в области нагревателя и термоприёмника.

Теоретическое обоснование метода представлено в работах [6–8].

Ограниченный стержень (неограниченная пластина) толщиной h₁ приведен в соприкосновение с полуограниченным стержнем, имеющим другие термические коэффициенты. Боковые поверхности стержней имеют тепловую изоляцию. В начальный момент времени на свободном конце стержня (пластины) начинает действовать источник тепла постоянной мощности q, который действует на протяжении всего процесса нагрева.

Требуется найти распределение температуры по длине стержней (по глубине пластины и тела) в любой момент времени [7].

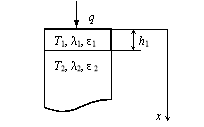
Рис. 1. Система, состоящая из ограниченного и полуограниченного тел

(1)

(3)

(4)

(5)

(6)

(7)

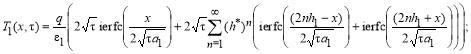
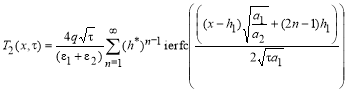(8, 9)

Введем следующие обозначения:

Выражения (8) и (9) в безразмерном виде:

(10,11)

Ряды в решениях (8), (9) и (10), (11) хорошо сходятся при малых значениях времени (Фурье).

При формула (10) имеет вид:

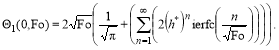(12)

При больших Fo выражение (12) имеет вид:

(13)

После ряда преобразований и упрощений при больших [7].:

(14)

Выражение (14) представляет собой линейную зависимость вида:

(15)

Решение (14), представляющее собой линейную зависимость (15), может быть применено при регуляризации теплового процесса в локальной области тела, расположенной вблизи нагревателя и термоприёмника.

Полученное решение (14) в форме, пригодной для использования на рабочем участке термограммы (при регуляризации теплового потока), было использовано для получения математических выражений для расчета толщины низкотеплопроводных покрытий на металлических основаниях.

Так как первый слой объекта (рис. 1) низкотеплопроводный, а второй — высокотеплопроводный, т. е. , тогда . Следовательно,

(17)

Из выражения (17) следует, что .(18)

Из выражения (18) можно определить толщину первого слоя объекта h₁.

Измерительная схема метода представлена на рис. 2.

Рис. 2. Измерительная схема метода

Тепловое воздействие на исследуемое тело с равномерным начальным температурным распределением осуществляется с помощью нагревателя постоянной мощности, выполненного в виде диска радиусом R, встроенного в подложку ИЗ. Подложка измерительного зонда изготовлена из теплоизолятора — пенополиуретана марки «Рипор». Температура в точке контроля измеряется с помощью термоэлектрического преобразователя (ТП).

Выражения для вычисления постоянной прибора, значения , при известной величинеимеют вид:

; .(19, 20)

Основные операции по определению.

1. Градуировка прибора: снятие термограммы на образце с известным значением λ_1о и величиной 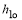; определение рабочего участка термограммы; расчет по этому участку коэффициента b_0o; расчет постоянной прибора В.
2. Определение толщины 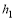покрытия исследуемого материала: снятие термограммы на исследуемом изделии; определение рабочего участка термограммы; расчет коэффициента b₀; расчет толщины h₁ покрытия по формуле (20).

Экспериментальные исследования. Структурная схема ИС, реализующей метод НК толщины покрытий в двухслойных полимерно-металлических изделиях, представлена на рис. 3.

Данная ИС предназначена для определения теплофизических свойств твердых материалов с повышенной точностью [9–11], для реализации метода неразрушающего определения температурных характеристик структурных переходов в полимерах [12–14] и может быть применена для определения толщины защитных покрытий на металлических основаниях.

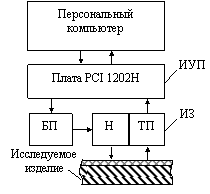
Рис. 3. Структурная схема ИС

ИС состоит из персонального компьютера, измерительно-управляющей платы, измерительного зонда, регулируемого блока питания. Зонд обеспечивает создание теплового воздействия на исследуемый образец с помощью нагревателя, температура в заданной точке контроля фиксируется термоэлектрическим преобразователем. Сбор информации производится при нагреве исследуемого тела.

Для экспериментальной проверки работоспособности разработанного метода и ИС определяли толщину покрытия из ПТФЭ на стальной пластине.

Испытаниям подвергали изделия с различными толщинами покрытий: h_1и = 0,95 мм (серия экспериментов № 1) и h_1и = 1,25 мм (серия экспериментов № 2). Для градуировки в качестве образцовой меры использовано изделие с толщиной покрытия из ПТФЭh_1о = 0,8 мм.

На рис. 4а представлена термограмма, зарегистрированная ТП при проведении градуировочного эксперимента (опыт № 1, табл. 1). Здесь T₁ — избыточная температура в точке контроля. На рис.4б показана зависимость Т = f(), по которой выделен рабочий участок термограммы.

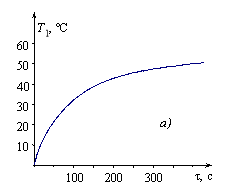
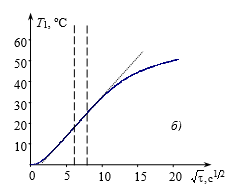
Рис. 4. Термограмма (а) и зависимость Т₁ = f() (б)

Для определения постоянной прибора В проведены пять градуировочных опытов, по результатам которых определено среднее значение В.

Таблица 1

Результаты градуировочного эксперимента

На рис. 5 представлены термограмма, зарегистрированная ТП при проведении опыта № 1 (табл. 2), и зависимость Т = f(), на которой выделен рабочий участок термограммы.

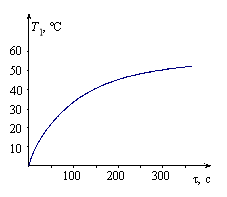
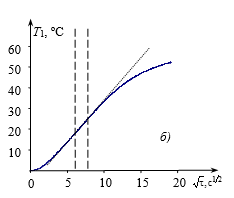
Рис. 5. Опыт № 1. Термограмма (а) и зависимость Т = f() (б).

В табл. 2 приведены результаты серий экспериментов № 1 и № 2.

Таблица 2

Результаты экспериментов на изделии спокрытием из ПТФЭ

Реализация математической модели и результаты экспериментов подтверждают работоспособность метода и ИС НК толщины полимерных, керамических и других низкотеплопроводных неметаллических покрытий на изделиях из металлов.

Литература:

1. Кудинов, В. А. Аналитические решения задач тепломассопереноса и термоупругости для многослойных конструкций: Учеб. пособие для вузов / Кудинов В. А., Карташов Э. М., Калашников В. В. — М.: Высшая школа. — 2005. — 430 с.
2. Теплофизические измерения и приборы / Е. С. Платунов, С. Е. Буравой, В. В. Курепин, Г. С. Петров; под общ. ред. Е. С. Платунова. — Л.: Машиностроение. — 1986. — 256 с.
3. Zhukov N. P., Mainikova N. F. Multimodel method of nondestructive determination of the thermophysical properties of solid materials // Journal of Engineering Physics and Thermophysics. Volume 76, Number 6 (2005). — P. 1104–1112.
4. Zhukov N. P., Mainikova N. F., Rogov I. V., Pudovkina E. V. Modeling of the process of heat transfer from a plane heat source of constant strength in thermophysical measurements // Journal of Engineering Physics and Thermophysics. Volume 85, Number 1(2012). — P. 203–209.
5. Определение условий адекватности модели распределения тепла в плоском полупространстве реальному процессу при теплофизическом контроле / Майникова Н. Ф., Жуков Н. П., Балашов А. А., Никулин С. С. // Вестник Тамбовского государственного технического университета. — 2006. — Т.12. № 3–1. — С. 610–616.
6. Лыков, А. В. Теория теплопроводности / А. В. Лыков. — М.: Высшая школа. — 1967. — 599 с.
7. Теоретическое обоснование теплового метода неразрушающего контроля двухслойных изделий / И. В. Рогов, Н. П. Жуков, Н. Ф. Майникова, Н. В. Лунева // Вопросы современной науки и практики. Университет им. В. И. Вернадского. — 2009. — № 9 (23) — С. 93–99.
8. Моделирование теплопереноса в методе неразрушающего контроля двухслойных материалов / Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов, А. О. Антонов // Вестник Тамбовского государственного технического университета. — 2013. — Т.19. № 3. — С. 506–511.
9. Жуков, Н. П. Измерительно-вычислительная система неразрушающего контроля теплофизических свойств / Н. П. Жуков, Н. Ф. Майникова // Приборы и техника эксперимента. — 2005, № 4. — С.164–166.
10. Мищенко, С. В. Информационно-измерительная система неразрушающего теплового контроля / С. В. Мищенко, Н. Ф. Майникова // Приборы. — 2009, № 4. — С. 20–24.
11. Estimation of systematic errors of the multimodel method for nondestructive determination of the termophysical properties of solid materials / N. P. Zhukov, N. F. Mainikova, I. V. Rogov, A. O. Antonov // Journal of Engineering Physics and Thermophysics. Vol. 87, No. 4. — 2014. — P.880–885.
12. Evaluation of random errors of the multimodel method for nondestructive determination of the termophysical properties of solid materials / N. P. Zhukov, N. F. Mainikova, I. V. Rogov, A. O. Antonov // Journal of Engineering Physics and Thermophysics. Vol. 87, No. 6, 2014. — P. 1398–1403. DOI 10.1007/s10891–014–1143–9.
13. Майникова, Н. Ф. Измерительная система и метод неразрушающего контроля структурных превращений в полимерных материалах/ Приборы и системы. Управление, контроль, диагностика. 2006. — № 1. — С 56–61.
14. Майникова, Н. Ф. Измерительная система неразрушающего контроля структурных превращений в полимерных материалах /Приборы и системы. Управление, контроль, диагностика. 2006. — № 9. — С 45–48.