Одно из направлений развития вычислительных технологий в настоящее время − это появление мощных математических пакетов, позволяющих максимально упростить процесс подготовки задачи, ее решения и анализа результатов. При использовании таких средств, как Maple [1], Mathcad, Mathematica или Matlab, решение дифференциального или трансцендентного уравнения, аналитическое либо численное дифференцирование и интегрирование, операции с матрицам, решение проблемы собственных значений, вычисление пределов, разложение в ряд и многие другие задачи решаются с помощью одной команды. Но, конечно, эту команду нужно правильно применить: надо корректно сформулировать задачу, знать в каком в виде искать решение и т. д. Иными словами, применение математических пакетов позволяет ускорить и упростить выполнение рутинных действий, выкладок и избавить от появления досадных ошибок, но математические пакеты не избавляют от необходимости думать.
Всеобщая компьютеризация коснулась и сферы образования. Внедрение вычислительной техники в учебный процесс поставило на повестку дня задачу создания учебников по различным дисциплинам, ориентированных на применение компьютеров и, в частности, на использование математических пакетов.
Например, широко распространенные учебники по вариационному исчислению [2–4] были написаны в 70-е годы прошлого столетия или даже раньше. Несомненно, они остаются прекрасными в научном и методическом плане книгами, но их авторы не предвидели и не могли предвидеть столь бурной компьютеризации, поэтому необходима адаптация курса вариационного исчисления к использованию современных компьютерных технологий.
Мною разработано учебно-методическое пособие «Вариационное исчисление» предназначенное для студентов всех форм обучения направления подготовки «Прикладная информатика» при изучении дисциплины «Теория оптимального управления». Данное учебно-методическое пособие посвящено методам решения классических вариационных задач.
Пособие содержит разделы «Основные понятия вариационного исчисления», «Вариационные задачи с фиксированными границами», «Вариационные задачи с подвижными границами», «Задачи на условный экстремум», «Достаточные условия экстремума», «Прямые методы в вариационных задачах», «Индивидуальное домашнее задание», «Приложение».
В каждом разделе кратко изложены теоретические сведения, содержащие основные определения и теоремы, приведены решения типовых примеров.
Поскольку ручное составление и решение уравнений (как правило, дифференциальных) связано с большими трудностями, и, как показывает опыт, плохо усваивается студентами. Поэтому при решении подобных задач мы применили систему компьютерной математики Maple, хорошо приспособленную к решению математических задач, требующих большого количества аналитических преобразований. Это самый первый пакет символьной математики. В настоящее время он является лидером среди универсальных систем символьных вычислений и пользуется особой популярностью в научной среде и предоставляет возможности для математических исследований любого уровня.
Разработала mws-файлы с подробными комментариями для каждого типа задач: вариационные задачи с фиксированными, подвижными границами и на условный экстремум.
Пример 1. Найти расстояние между параболой 
и прямой 
.
Решение: Эта задача с подвижными границами. Задача сводится к нахождению экстремального значения функционала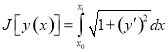
, при условии, что левый конец экстремали может перемещаться по кривой 
, а правый — по прямой 
.
1. Задаем подынтегральную функцию:
> restart:
> F:=(x,Y,DY)->sqrt(1+DY^2);
> x0:=X0;x1:=X1;
2. Задаем две фиксированные кривые 
и 
, находим их производные:
> F1:=(x)->x^2; dF1:=diff(F1(x),x);
> F2:=(x)->x-5; dF2:=diff(F2(x),x);
3. Составляем функционал:
> J:=int(F(x,y(x),diff(y(x),x)),x=x0..x1);
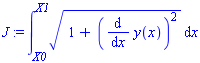
4. Записываем основную формулу уравнения Эйлера:
> eq:=diff(F(x,Y,DY),Y)-diff(diff(F(x,Y,DY),x),DY)-diff(diff(F(x,Y,DY),Y),DY)*DY-diff(F(x,Y,DY),DY$2)*D2Y=0;
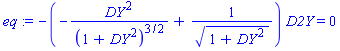
5. Выполняемзамены (оператор subs) 
:
> eq1:=subs(Y=y(x),DY=diff(y(x),x),D2Y=diff(y(x),x$2),eq);
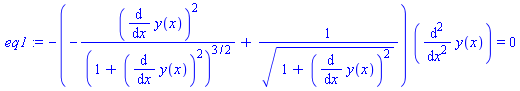
6. Находим общее решение уравнения Эйлера:
> rez:=dsolve(eq1);
>assign(rez):y(x):
7.Записываем условия трансверсальности:
> dFdY:=diff(F(x,Y,DY),DY);
> df:=subs(Y=y(x),DY=diff(y(x),x),D2Y=diff(y(x),x$2),dFdY):
> us_t1:=F(x,y(x),diff(y(x),x))+(dF1-diff(y(x),x))*df=0;
> us_t2:=F(x,y(x),diff(y(x),x))+(dF2-diff(y(x),x))*df=0;
> a:=subs(x=x0,us_t1);
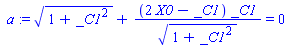
> b:=subs(x=x1,us_t2);
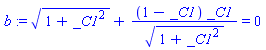
8.Записываем граничные условия 
, 
> left:=subs(x=x0,y(x))=F1(x0);
> right:=subs(x=x1,y(x))=F2(x1);
9. Находим
,
, 
, 
и экстремаль:
> rez1:=solve({left,right,a,b});
> y(x):=subs(rez1,y(x));assign(rez1);
10.Находим значение функционала при полученном решении:
> F(x,y(x),diff(y(x),x)):
>J;
Пример 2. Найти экстремаль функционала 
, удовлетворяющую граничным условиям 
и интегральным связям 
, 
.
Решение: Это изопериметрическая задача.
1. Задаем подынтегральную функцию и граничные условия:
> restart:
> F:=(x,Y,DY)->DY^2;
> x0:=0;x1:=1;y0:=0;y1:=0;
2. Составляем функционал:
> J:=int(F(x,y(x),diff(y(x),x)),x=x0..x1);
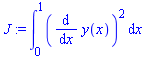
3.Составляем функцию Лагранжа. Т. к. 
, 
, 
, то
> H1:=(x,Y,DY)->Y;H2:=(x,Y,DY)->x*Y;
> F1:=(x,Y,DY)->F(x,Y,DY)+l1*H1(x,Y,DY)+l2*H2(x,Y,DY);
4. Записываем основную формулу уравнения Эйлера:
> eq:=diff(F1(x,Y,DY),Y)-diff(diff(F1(x,Y,DY),x),DY)-diff(diff(F1(x,Y,DY),Y),DY)*DY-diff(F1(x,Y,DY),DY$2)*D2Y=0;
5. Выполняемзамены (оператор subs): :
> eq1:=subs(Y=y(x),DY=diff(y(x),x),D2Y=diff(y(x),x$2),eq);
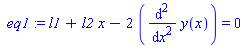
6. Находим общее решение уравнения Эйлера:
> dsolve(eq1,y(x));
7. Составляем краевую задачу:
> tk:={eq1,y(x0)=y0,y(x1)=y1};
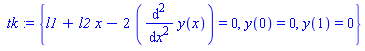
8. Решаем краевую задачу (оператор dsolve):
> S:=dsolve(tk,y(x));
> assign(S):y(x):
9. Из уравнений связей находим l1,l2
> a1:=int(H1(x,y(x),diff(y(x),x)),x=x0..x1)=1; a2:=int(H2(x,y(x),diff(y(x),x)),x=x0..x1)=0;
> L:=solve({a1,a2});
10.Находим значение функционала при полученном решении:
> y(x):=subs(L,y(x));
> F(x,y(x),diff(y(x),x)):
> J;
Участие в процессе обучения одновременно педагога и компьютера значительно улучшает качество образования. Использование возможностей системы Mapleактивизирует процесс преподавания, повышает интерес студентов к изучаемой дисциплине и эффективность учебного процесса, позволяет достичь большей глубины понимания учебного материала.
Литература:
- Шевченко, А. С. Использование математического пакета Maple при проведении лабораторных работ по курсу «Численные методы» / А. С. Шевченко // Молодой ученый. − 2015. − № 9. − С. 1222–1225.
- Гельфанд, И. М. Вариационное исчисление/ И. М. Гельфанд, С. В. Фомин. − М.: Физматлит, 1961.
- Краснов, М. Л. Вариационное исчисление: задачи и упражнения: учебное пособие для втузов / М. Л. Краснов, Г. И. Макаренко, А. И. Киселев. — М.: Наука, 1973. — 190 с.
- Эльсгольц, Л. Э. Дифференциальные уравнения и вариационное исчисление: Учебник для физ. спец. ун-тов/ Л. Э. Эльсгольц — М.: Наука, 1969. –424 с.
