Введение. В настоящей статье предлагается вариант концептуальной модели архитектуры информационной системы численного моделирования процессов рассеяния оптических волн, расчета и обработки дифракционных картин, позволяющей использовать различные численные методы решения прямой дифракционной задачи.
Применение проектируемой информационной системы возможно для научных исследований с целью выявления и исследования закономерностей и явлений, возникающих в ходе процесса рассеяния электромагнитных волн. Известно, что в настоящее время построены аналитические физ.-мат. модели процессов рассеяния оптических волн в дальней и ближней зонах Френеля, но, между тем, исследование данных процессов в средней зоне представляет известный научный и практический интерес: явления, происходящие в ходе данного процесса недостаточно изучены, отсутствуют аналитические методы и модели, позволяющие исследовать данную проблему. В связи с этим, численное моделирование процесса рессеяния в средней зоне позволит глубже исследовать данную проблему.
В силу того, что система позволяет моделировать процессы рассеяния, используя различные численные физ.-мат. модели, в том числе удовлетворяющие условию быстродействия в режиме реального времени, применение системы возможно и для решения инженерных задач, таких как дистанционный контроль и бесконтактное определение состояния и динамики изменения свойств материалов поверхностей.
Физико-математическая модель процессов рассеяния. Синтез оптико-электронных систем, применяющих дифракционные методы, требует использования эффективных численных моделей распространения частично когерентных волн, рассеянных на пространственно-случайном рассеивателе [1]. В настоящее время известны несколько физ.-мат. моделей процессов рассеяния на отражающих поверхностях, которые основываются на различных физических принципах и математических моделях. Выбор физ.-мат. модели, наиболее точно описывающей рассеяние оптического излучения при заданных условиях, определяется характеристиками источника излучения и рассеивающей поверхности, а также принципами и структурой измерительных схем [2].
В общем виде распределение рассеянных полей описывается следующим дифференциальным волновым уравнением:
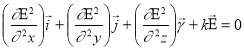 ,(1)
,(1)
граничные условия для которого определяются исходя из геометрических характеристик поверхности объекта и электродинамических параметров его материала. Специфика получаемых решений определяется граничными условиями данного уравнения. В связи с тем, что в реальном мире существует множество классов поверхностей с разнообразными геометрическими характеристиками и электродинамическими параметрами, весьма затруднительно выработать единую теорию, достаточно полно описывающую процессы рассеяния для всех видов рассеивающих объектов. Однако, существуют аналитические физ.-мат. модели, описывающие процесс рассеяния при определенных условиях, накладываемых как на параметры рассеиваемого излучения, так и на характеристики рассеивающего объекта. В наибольшей степени разработаны две из таких моделей: приближение Релея и приближение Кирхгофа.
Модель поверхностного рассеяния Релея. Рассмотрим случай, когда рассеивающая поверхность достаточно гладкая, тогда излучение, приходящее с направления ![]() , отражается только в направлении
, отражается только в направлении ![]() ,
, ![]() [3]. Граничные условия для уравнения распределения рассеянных полей заключаются в том, что поле в пространстве представляется неограниченным и аппроксимируется бесконечной суммой плоских волн. Рассеяние в таких условиях дает возможность получения данных о профиле поверхности при больших углах падения и рассеяния электромагнитного излучения [2]. Двумерная функция распределения коэффициента отражения при рэлеевском рассеянии является дельта-функцией и определяется соотношением
[3]. Граничные условия для уравнения распределения рассеянных полей заключаются в том, что поле в пространстве представляется неограниченным и аппроксимируется бесконечной суммой плоских волн. Рассеяние в таких условиях дает возможность получения данных о профиле поверхности при больших углах падения и рассеяния электромагнитного излучения [2]. Двумерная функция распределения коэффициента отражения при рэлеевском рассеянии является дельта-функцией и определяется соотношением
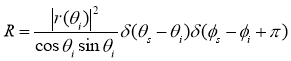 ,(2)
,(2)
где ![]() – амплитудный коэффициент отражения Френеля, соответствующий углу падения
– амплитудный коэффициент отражения Френеля, соответствующий углу падения ![]() .
.
Для строгого определения класса поверхностей, для которых применима данная модель, используется критерий Релея, характеризующий степень шероховатости рассеивающей поверхности:
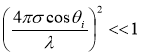 ,(3)
,(3)
где ![]() – среднеквадратичное отклонение высоты профиля от средней линии,
– среднеквадратичное отклонение высоты профиля от средней линии, ![]() – длина волны рассеиваемого оптического излучения,
– длина волны рассеиваемого оптического излучения, ![]() – угол падения подсвечивающей волны. Следовательно, как показано в [3], поверхность может считаться достаточно гладкой, если
– угол падения подсвечивающей волны. Следовательно, как показано в [3], поверхность может считаться достаточно гладкой, если
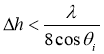 ,(4)
,(4)
где ![]() – отклонение высоты профиля от средней линии. Если провести анализ этих двух приведенных неравенств, то можно утверждать, что для электромагнитного излучения оптического диапазона (
– отклонение высоты профиля от средней линии. Если провести анализ этих двух приведенных неравенств, то можно утверждать, что для электромагнитного излучения оптического диапазона (![]() ) колебания
) колебания ![]() не должны превышать 60 нм. Также можно заметить, что приведенный критерий гладкости легче удовлетворить при больших значениях
не должны превышать 60 нм. Также можно заметить, что приведенный критерий гладкости легче удовлетворить при больших значениях ![]() , чем в случае нормального падения лучей, поэтому сравнительно неровные поверхности на практике могут рассматриваться как достаточно гладкие при скользящем облучении.
, чем в случае нормального падения лучей, поэтому сравнительно неровные поверхности на практике могут рассматриваться как достаточно гладкие при скользящем облучении.
Модель поверхностного рассеяния Кирхгофа. Теперь рассмотрим шероховатую поверхность со случайным распределением неровностей как совокупность различным образом ориентированных плоскостей, каждая из которых имеет определенную точку касания с исходной поверхностью, т.е. используем модель представления шероховатой поверхности аппроксимацией касательными плоскостями. Также примем во внимание следующие ограничения: поле вне экрана равно нулю, поле не взаимодействует с экраном и обратное распределение поле в соответствии с принципом Гюйгенса-Френеля не учитывается. Пусть система координат такова, что оптическая волна распространяется от источника вдоль оси ![]() и источник расположен в плоскости параллельной плоскости
и источник расположен в плоскости параллельной плоскости ![]() (
(![]() ), то есть
), то есть ![]() является константой. Тогда, согласно [4], решение волнового уравнения распределения рассеянных электромагнитных полей можно представить в виде:
является константой. Тогда, согласно [4], решение волнового уравнения распределения рассеянных электромагнитных полей можно представить в виде:
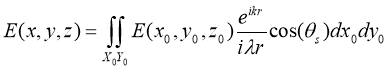 ,(5)
,(5)
где ![]() – значение интенсивности э/м поля в точке
– значение интенсивности э/м поля в точке ![]() источника излучения,
источника излучения, ![]() – длинна волны,
– длинна волны, ![]() – площадь отверстия,
– площадь отверстия, ![]() – расстояние между точкой
– расстояние между точкой ![]() на приемнике излучения и точкой
на приемнике излучения и точкой ![]() источника,
источника, ![]() – угол, задающий направление на точку наблюдения
– угол, задающий направление на точку наблюдения ![]() , величина
, величина ![]() – волновое число. Если принять во внимание, что
– волновое число. Если принять во внимание, что
![]() ,(6)
,(6)
то выражение (5) можно представить в виде:
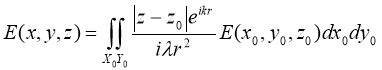 ,(7)
,(7)
или, для дискретного случая, в виде:
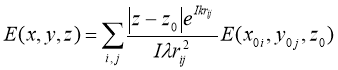 ,(8)
,(8)
где через ![]() обозначена мнимая единица.
обозначена мнимая единица.
В отличие от модели поверхностного рассеяния Релея, дифракционная модель Кирхгофа применима на шероховатых поверхностях, не удовлетворяющих критерию Релея (3). На гладких поверхностях модель Кирхгофа дает те же результаты, что и модель Релея, однако обладает большей вычислительной сложностью. На очень грубых поверхностях обе модели не соответствуют экспериментально полученным данным [2]. Таким образом, выбор конкретной физико-математической модели при моделировании процессов рассеяния определяется геометрическими характеристиками рассеивающей поверхности, в первую очередь степенью шероховатости (![]() ), а также пространственным соотношением источника и приемника излучения (углы
), а также пространственным соотношением источника и приемника излучения (углы ![]() и
и ![]() ).
).
Архитектура ИС моделирования процессов рассеяния. Проектирование и разработка программ, реализующих модели физических процессов и явлений достаточно сложны и трудоемки. Одним из подходов, обеспечивающих структурирование математической модели и упрощение ее программирования, является объектно-ориентированный подход, в котором реальный физический процесс или система представляются совокупностью объектов, взаимодействующих друг с другом. В ходе объектно-ориентированного анализа предметной области использовался метод неформального описания [7]. Формализация моделируемого явления рассеяния оптического излучения на поверхности и дифракции проводилась в три этапа.
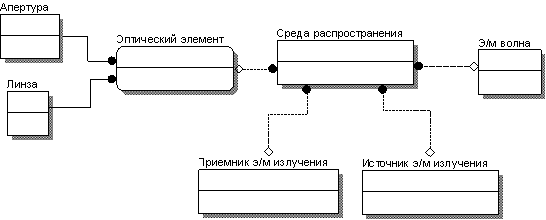
На первом этапе проводилось построение информационной модели, абстрагирование реальных сущностей в терминах объектов и атрибутов, то есть построение модели "сущность-связь" проектируемой системы. На данном шаге были выделены основные сущности моделируемой системы, такие, как электромагнитная волна, зондируемый объект, источник и приемник электромагнитного излучения, апертура и среда распространения (Рис. 1).
|
|
|
Рис. 1. Диаграмма сущность-связь ИС численного моделирования процессов рассеяния |
Проведенный системный анализ предметной области позволяет утверждать, что математические модели перечисленных сущностей могут представляться в виде функционально заданных величин, характеризующих моделируемые понятия предметной области с заданной степенью абстракции [8]. Следовательно, можно выделить такую сущность, которая будет представлять собой произвольную комплексную вектор-функцию в n-мерном пространстве. Используемые в процессе моделирования функции можно разделить на два класса: аналитически заданные функции и численные функции, заданные таблицей соответствия её значений определеннам аргументам области определения. В рамках проектируемой системы моделирования функции представляют собой однозначное отображение одного множества на другое.
![]() ,(9)
,(9)
где ![]() – область определения функции,
– область определения функции, ![]() – область значений функции.
– область значений функции.
Множества определения и значений функций также являются сущностями проектируемой системы моделирования и называются доменами значений или множествами допустимых значений. В качестве элементов множеств могут выступать точки n-мерного пространства, то есть используемые в процессе моделирования функции ограничиваются классом вектор-функций. Следовательно, ещё одной основной сущностью, необходимой для построения информационной системы моделирования процессов рассеяния, является точка, представляемая в виде вектора её координат. Применение вектор-функций позволит использовать одну программную сущность, абстрагирующую функциональную зависимость, для задания нескольких характеризующих моделируемую физическую сущность функциональных величин, определенных на одной области определения (домене). Например, волна может быть задана в некоторой области пространства при помощи определения характеризующих её функций амплитуды и фазы, которые задаются таблицами соответствующих значений амплитуды и фазы в точках принадлежащих одному множеству точек моделируемого пространства.
Таким образом, используемые в процессе моделирования сущности можно разделить на две группы: сущности, отражающие понятия предметной области, в данном случае процесса распространения электромагнитного излучения оптического диапазона, и сущности, необходимые для организации процесса моделирования, отражающие элементы и понятия математического аппарата, применяемого для формализации понятий и явлений предметной области.
Второй этап формализации предметной области заключался в выработке архитектурного решения и основных принципов построения системы моделирования. В ходе проектирования архитектурного решения, были выделены следующие структуры, образующие архитектуру разрабатываемой системы: модульные структуры декомпозиции и вариантов использования, типовая и структурная модели ИС.
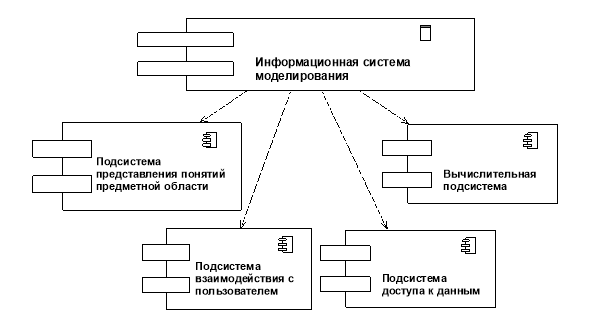
Модульная декомпозиция архитектуры информационной системы тесно связана с анализом предметной области и задач, стоящих перед авторами. Модульная структура представляет декомпозицию архитектуры проектируемой системы на отдельные части: подсистемы и блоки реализации, которые входят в состав проектируемой системы. К ним можно отнести следующие модули: подсистему взаимодействия с пользователем, подсистему представления понятий предметной области, вычислительную подсистему, и подсистему доступа к данным (Рис. 2).
|
|
|
Рис. 2. Модульная структура ИС моделирования процессов рассеяния |
Подсистема взаимодействия с пользователем выполняет функции организации контекста взаимодействия с пользователями системы и реализации пользовательского интерфейса. В свою очередь, данную подсистему можно декомпозировать на модуль ввода параметров, определяющих процедуры расчета и моделирования явлений предметной области, и модуль графического вывода, предназначенный для визуального представления результатов моделирования.
![]() Подсистема доступа к данным предназначена для организации механизмов хранения и получения данных из хранилища, а также включает инструментарий поиска данных по заданным критериям и их предобработки. Данная подсистема служит посредническим шлюзом между ядром информационной системы моделирования –подсистемой представления понятий предметной области и системой хранения данных, обеспечивающей доступ к репозитарию данных.
Подсистема доступа к данным предназначена для организации механизмов хранения и получения данных из хранилища, а также включает инструментарий поиска данных по заданным критериям и их предобработки. Данная подсистема служит посредническим шлюзом между ядром информационной системы моделирования –подсистемой представления понятий предметной области и системой хранения данных, обеспечивающей доступ к репозитарию данных.
Функциональным ядром разрабатываемой системы моделирования является вычислительная подсистема, которая предназначена для выполнения процедур численного моделирования физических процессов распространения оптического излучения. Данная подсистема включает в себя множество алгоритмов проведения численных экспериментов для различных физико-математических моделей процессов рассеяния, а также содержит инструменты анализа информации, содержащейся в данных, полученных в ходе процесса моделирования или из хранилища данных.
Подсистема представления понятий предметной области – структурное ядро системы и являет собой объединение структур данных и алгоритмов предназначенных для численного представления понятий и явлений моделируемой предметной области, таких как электромагнитная волна, различные оптические элементы, среды распространения и пр. (Рис. 1). Данные программные абстракции физических и математических сущностей могут участвовать в процессе численного эксперимента и моделирования под управлением разрабатываемой информационной системы. Подсистему представления понятий предметной области можно разбить на две логические части: подсистему инструментария моделирования (ПИМ) и подсистему моделирования предметной области (ПМПО).
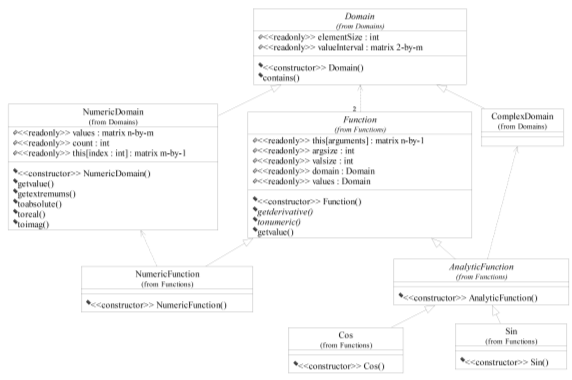
- ПИМ призвана обеспечить необходимую программную среду для проведения численных вычислений и предоставляет необходимые структуры данных и алгоритмы для представления понятий математического аппарата, используемого при построении физ.-мат. моделей процессов рассеяния и моделей участвующих в этих процессах физических объектов. Как было показано выше, одним из основных инструментов, используемых при математическом описании физических процессов, является функция, которая применяется для задания характеристик объектов и явлений (Рис. 3).
|
|
|
Рис. 3. Диаграмма основных классов подсистемы инструментария моделирования |
|
|
|
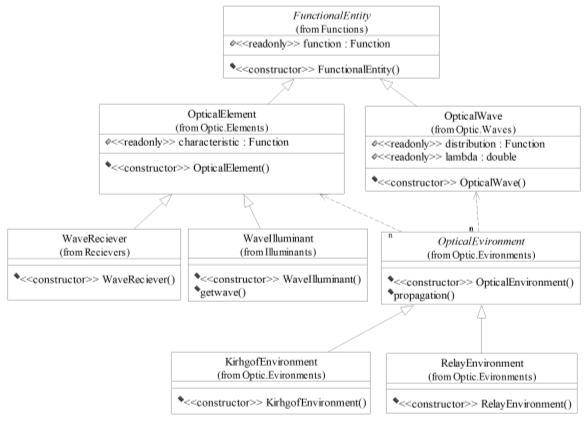
Рис. 4. Диаграмма основных классов подсистемы моделирования предметной области |
- ПМПО реализует необходимые программные структуры данных и алгоритмы поведения физико-математических моделей объектов предметной области в ходе численного эксперимента. На Рис. 4 представлены основные классы, абстрагирующие центральные понятия процесса рассеяния оптического излучения: оптическая волна, оптический элемент и среда распространения. Апертура, линзы, источник и приемник излучения являются оптическими элементами, которые, как и оптическая волна, используются объектами классов пространств при проведении численного эксперимента моделирования процесса рассеяния.
В силу наукоемкости и вычислительной сложности используемых алгоритмов для реализации программных компонент ИС использовалось такое современное средство решения сложных физико-математических задач, как пакет прикладных программ Matlab.
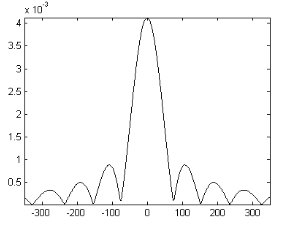
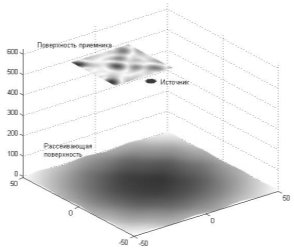
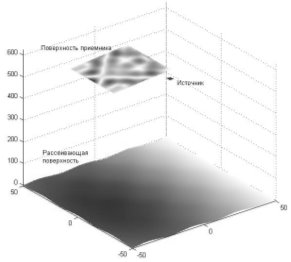
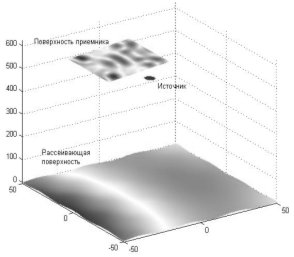
Примеры использования. С целью подтверждения применимости ИС для проведения моделирования процессов рассеяния был проведен ряд численных экспериментов, которые показали результаты, схожие с получаемыми на практике. В качестве физико-математической модели процесса рассеяния использовалась модель Кирхгофа, позволяющая получить наиболее точные результаты. Расчеты проводились для одномерного и двумерного случаев с параллельным и непараллельным положением излучателя и приемника и для различных типов апертур (Рис. 6–13).
На данных рисунках изображено пространственное распределение интенсивности электромагнитных рассеянных полей на рассеивающей поверхности и приемнике излучения: темные области – наибольшая интенсивность электромагнитного поля. Численный эксперимент проводился при следующих условиях:
а) длина волны принята равной единице с целью уменьшения погрешности вычисления, все линейные размеры на рисунках представлены в длинах волн;
б) расстояние от источника до рассеивающей поверхности ![]() = 500 длин волн;
= 500 длин волн;
в) расстояние от рассеивающей поверхности до приемника излучения равно 625 длин волн;
г) линейные размеры источника излучения равны 3 длины волны в одномерном случае и 3х3 длины волны в двумерном случае;
д) линейные размеры рассеивающей поверхности равны 750 длин волн в одномерном случае и 100х100 длин волн в двумерном случае;
е) линейные размеры поверхности приемника равны 750 длин волн в одномерном случае и 50х50 длин волн в двумерном случае;
ж) угол наклона источника к рассеивающей поверхности составляет 0˚ для Рис. 5, 9, 10 и -30˚ для Рис. 7, 11, 12;
з) угол наклона приемника к рассеивающей поверхности составляет 0˚ для Рис. 6, 9, 10 и -30˚ для Рис. 7, 11, 12.
|
|
|
|
|
Рис. 5. Распределение поля на рассеивающей поверхности (одномерный случай, источник параллелен поверхности) |
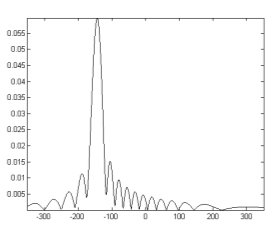
Рис. 6. Распределение поля на приемнике (одномерный случай, приемник параллелен рассеивающей поверхности) | |
|
| ||
|
|
|
|
|
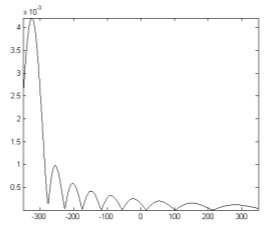
Рис. 7. Распределение поля на рассеивающей поверхности (одномерный случай, источник под углом -30˚ к поверхности) |
|
Рис. 8. Распределение поля на приемнике (одномерный случай, приемник под углом 30˚ к рассеивающей поверхности) |
|
|
|
|
|
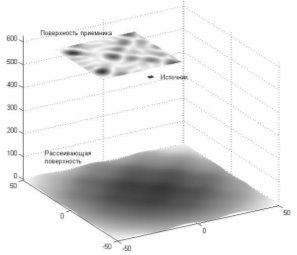
Рис. 9. Распределение поля на рассеивающей поверхности и приемнике излучения (двумерный случай, источник и приемник параллельны поверхности, апертура прямоугольная) |
Рис. 10. Распределение поля на рассеивающей поверхности и приемнике излучения (двумерный случай, источник и приемник параллельны поверхности, апертура эллиптическая) | |
|
| ||
|
|
|
|
|
Рис. 11. Распределение поля на рассеивающей поверхности (двумерный случай, источник и приемник под углом 30˚ к поверхности, апертура прямоугольная) |
|
Рис. 12. Распределение поля на приемнике (двумерный случай, источник и приемник под углом 30˚ к рассеивающей поверхности, апертура эллиптическая) |
Заключение. Применение системного и объектно-ориентированного подходов к проектированию и реализации системы моделирования процесса рассеяния электромагнитного излучения позволяет проводить численные эксперименты с физическими процессами и системами, обеспечивая легкую и быструю модернизацию и модификацию созданной модели в соответствии с возникающими в процессе научно-исследовательской деятельности целями и задачами. Предложенное архитектурное решение позволяет найти решения для поставленных авторами научно-исследовательских задач, и является применимым для создания информационной системы моделирования процессов распространения оптического излучения, которая будет способна проводить численные эксперименты с целью детального исследования вопросов и закономерностей распространения оптических волн и процессов дифракции света.
Библиографический список
- Проскурин Д. К., Печенкин Н. С. Сравнительный анализ численных моделей дифракции. Системы управления и информационные технологии, Воронеж 2006, N3(25), с. 85-87.
- Проскурин Д. К. Выделение пространственных неоднородностей в оптических полях, рассеяных на технологически обработанных поверхностях. Дисс. канд. физ.-мат. н., Воронеж, 2000.
- Рис У. Основы дистанционного зондирования. М.: Техносфера, 2006.
- Гудмен Дж. Введение в Фурье-оптику. М.: Мир, 1970.
- Короленко В. П., “Оптика когерентного излучения”; Москва, 1997.
- Басс Л., Клементс П., Кацман Р. Архитектура программного обеспечения на практике. 2-е издание. – СПб.: Питер, 2006.
- Буч Г., Объектно-ориентированное проектирование с примерами применения: Пер. с англ. - М.: Конкорд, 1992.
- Горстко А.В. Познакомьтесь с математическим моделированием. М.: Знание, 1991.
- Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика. Первый семестр: Интерактивный компьютерный учебник / Иван. гос. энеpг. ун-т. – Иваново, 2002.
- Вендров А.М. CASE -технологии. Современные методы и средства проектирования информационных систем. М.: Финансы и статистика, 1998. 176 с.