Математические методы в эконометрике как средства анализа и исследования социально-экономических систем
Автор: Звягин Леонид Сергеевич
Рубрика: Экономическое развитие и рост
Опубликовано в Вопросы экономики и управления №1 (1) июль 2015 г.
Дата публикации: 24.06.2015
Статья просмотрена: 3846 раз
Библиографическое описание:
Звягин, Л. С. Математические методы в эконометрике как средства анализа и исследования социально-экономических систем / Л. С. Звягин. — Текст : непосредственный // Вопросы экономики и управления. — 2015. — № 1 (1). — С. 1-6. — URL: https://moluch.ru/th/5/archive/10/210/ (дата обращения: 02.05.2024).
Методы эконометрики являются самыми современными средствами анализа и исследования различных социально-экономических систем. С помощью эконометрических методов можно отклонить некоторые экономические гипотезы или показать невозможность применения в конкретных условиях. Хотя средства эконометрики не позволяют доказать теоретические утверждения, но за счет ее методов можно показать, что то или иное утверждение не противоречит данным наблюдений. Овладев элементарным инструментарием эконометрики, можно обоснованно прогнозировать развитие этих систем, оценивать влияние решений или правительственных постановлений об изменении цен, налогов и т. д. на положение дел любого предприятия, разрабатывать пути эффективного управления ими, принимать эффективные управленческие решения.
Ключевые слова: математические методы, экономика, анализ, эконометрика, эффективность, управление.
Methods of econometrics are the most modern means of analysis and study of different socio-economic systems. Using econometric methods, you can reject some economic hypotheses or to show the impossibility of application in specific conditions. Although tools of econometrics does not allow to prove the theoretical assertion, but at the expense of its methods it is possible to show that the assertion does not contradict the observed data. Having mastered the basic tools of econometrics, can be reasonably predict the development of these systems, to assess the impact of decisions or government regulations on price changes, taxes, etc. on the state of Affairs of any enterprise, to develop ways to effectively manage it, to make effective management decisions.
Keywords: mathematical methods, Economics, analysis, econometrics, efficiency, management.
1. Исторические сведения о становлении науки эконометрики.
В начале XX века тенденции развития экономических теорий в условиях непрерывно растущей сложности социально-экономических процессов, бурного развития науки и промышленности, форм хозяйствования и, как следствие, усложнения управленческих функций, практически на всех уровнях иерархии экономических систем, обусловило появление нового направления в науке о социально-экономические явлениях. В некоторых странах были попытки составить так называемые «барометры развития». Самый известный из них «гарвардский барометр», с помощью которого в 20-е годы пытались предсказать поведение товарного и денежного рынка.
Гарвардская школа считалась в то время центром экономических исследований. Здесь впервые начали системно изучать ряды экономических показателей с учетом взаимосвязи между ними и на основе этих показателей исследовать тенденции и циклы экономических процессов. Кризис 1929–1933 гг. заставил критически пересмотреть методы анализа, которые применялись в то время в экономике. [3]
Лишь после того как в экономических исследованиях начали учитывать случайные аспекты экономических явлений, стало возможным формирование эконометрики как отрасли экономической науки.
Современные методы математической статистики начали применять в биологии. В конце XIX в. английский биолог К. Пирсон исследовал кривые распределения некоторых числовых показателей человеческого организма. Позже он и его школа начали изучать корреляции в биологии и строить линейные регрессии. Подходы, предложенные биологами, были применены в экономике. В 1897 появилась работа В. Парето, в которой исследовались доходы населения в разных странах. В ней впервые была применена так называемая кривая Парето, параметры которой были получены статистическими методами. [5]
В начале XX в. вышло несколько работ английского статистика Гукера, в которых с помощью корреляционно-регрессионных методов, основанных школой Пирсона, изучались взаимосвязи между экономическими показателями, в частности влияние банкротств на товарной бирже на цену зерна. Позже появилось много работ как по развитию теории математической статистики и ее прикладных элементов, так и по практическому применению этих методов в экономическом анализе. Прежде всего, это труды Мура, вышедшие в течение 1914–1917 гг. В 1928 было опубликовано исследование Ч. Кобба и П. Дугласа о производственной функции, которая вошла в эконометрику как классический пример и до сих пор является важным инструментом эконометрического анализа. Именно эти работы заложили основы современной эконометрики.
Эконометрика как отдельная отрасль науки известна под таким названием только с 1930 года. Именно тогда была основана эконометрическое общество, которое определяло себя так: «Международное общество для развития экономической теории и ее связи со статистикой и математикой». Основоположниками эконометрики считают Р. Фриша, Е. Шумпетера, Я. Тинбергена — последователей неоклассической экономической школы и кейнсианства. Они одними из первых целенаправленно пытались совместить экономическую теорию с математическими и статистическими методами. Сначала ученые ограничивались изучением некоторых моделей спроса и предложения. Только после Второй мировой войны они начали изучать комплексные эконометрические модели на макро уровне, в которых основное внимание уделялось спросу, финансовому состоянию и налогам, прибыли, ценам и т. п. Основным вкладом этих ученых в эконометрическую науку является разработка эконометрических моделей принятия решений, за которую в 1969 г.г. Фриш и Я. Тинберген были отмечены Нобелевской премией. [3]
Позже Нобелевскую премию в области экономики получили Т. К. Купманс (1975) за разработку линейных эконометрических моделей и развитие статистических методов в эконометрике, Л. Р Клейн (1980) за разработку сложных эконометрических моделей и их применение для анализа конъюнктурных колебаний и экономической политики, Т. Хаавельмо (1989) за разработку и применение теоретико-вероятностных методов для анализа взаимосвязанных эконометрических структур. Значительный вклад в разработку экономических моделей сделали также нобелевские лауреаты В. Леонтьев (1973), которому принадлежат разработки в области балансовых моделей для моделирования взаимосвязей с большим количеством переменных, Л. Канторович (1975), который исследовал производственные модели, Г. Дебре (1983), который работал в области математизации экономической теории. Хотя их труды непосредственно не связаны с эконометрическими исследованиями, все они в значительной степени повлияли на дальнейшее развитие не только эконометрики, но и экономической науки в целом. В 2000г. Дж. Хекман и Д. Макфеден отмечены Нобелевской премией за разработку микро эконометрики и методов статистического анализа. [7]
Слово «эконометрика» буквально означает «измерения в экономике», что дает основания под этим термином понимать все, что связано с измерениями в экономике. Однако такое толкование очень широкое и не отражает особенностей этой области знаний. С другой стороны, из-за необходимости применения математических методов иногда эконометрике дают узкое толкование, а именно рассматривают ее только как определенный набор математико-статистических средств, которыми количественно исследуют взаимосвязи определенных рядов статистических данных. Поэтому точнее будет такое определение [1]: эконометрика — это самостоятельная научная дисциплина, которая объединяет совокупность теоретических результатов, средств, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории, экономической статистики и математико-статистического инструментария придавать конкретных количественных значений общим (качественным) закономерностям, обоснованным экономической теорией.
Относительно данного определения следует иметь в виду, что задача экономической теории в пределах эконометрики заключаются не только в том, чтобы выявлять законы и связи, которые объективно существуют в экономике, но и описывать их математическими методами. Экономическая статистика аккумулирует всю информацию об экономических процессах, происходящих в реальной экономике, и олицетворяет тот практический опыт, который должен подтвердить или опровергнуть соответствующие экономические теории. А под математико-статистическим инструментарием понимают не всю математическую статистику, а лишь отдельные ее разделы: линейные модели регрессионного анализа, анализ временных рядов, построение и анализ систем одновременных уравнений, проверку статистических гипотез. [2]
Именно «приземление» экономической теории на базу конкретной экономической статистики и получение с помощью соответствующих математических методов количественных взаимосвязей между экономическими показателями являются сущностью эконометрики.
Указанные таким образом ключевые моменты в определении эконометрике обеспечивают ее разграничения с такими дисциплинами, как математическая экономика, описательная экономическая статистика и математическая статистика. Математическая экономика — это математически сформулированная экономическая теория, изучающая связи между экономическими переменными на общем (неколичественном) уровне. Она становится эконометрикой, когда символически представленные в уравнениях коэффициенты заменяют конкретными числовыми оценками, полученными на базе соответствующих статистических данных (данных описательной статистики) методами математической статистики.
Процесс эконометрического моделирования состоит из следующих шагов:
1) выбор конкретной формы аналитической зависимости между экономическими показателями (спецификация модели) на основании соответствующей экономической теории;
2) сбор и подготовка статистической информации;
3) оценка параметров моделей;
4) проверка адекватности модели и достоверности ее параметров;
5) применение модели для прогнозирования развития экономических процессов с целью дальнейшего управления ими. [5]
Итак, эконометрика — это прикладная экономико-математическая дисциплина, которая изучает методы количественного измерения взаимосвязей между экономическими показателями и направления их применения в экономических исследованиях и практической экономической деятельности.
3. Использование математического аппарата в эконометрике.
Во многих задачах требуется установить и оценить зависимость некоторого экономического показателя от одного или нескольких других показателей. Очевидно, любые экономические показатели, как правило, находятся под влиянием случайных факторов, а потому с математической точки зрения интерпретируются как случайные величины. Из теории вероятностей известно, что случайные величины могут быть связаны функциональной или статистической зависимостью или вообще быть независимыми. Строгая функциональная зависимость реализуется в экономике редко. Чаще наблюдается так называемая статистическая зависимость. Статистическая зависимость, когда с изменением одной случайной величины изменяется закон распределения вероятностей другой. Корреляционная зависимость статистическая зависимость, которая проявляется в том, что с изменением одной величины изменяется среднее значение другой.
Можно отметить два типа взаимосвязи переменных. В одном случае неизвестно, какая из переменных независимая, а какая — зависимая, то есть они равноправны и связь можно рассматривать как в одну, так и в другую сторону. Во втором случае переменные неравноправные, то есть изменения лишь одной из них влияет на изменение другой, а не наоборот. В этом случае при рассмотрении связи между двумя переменными величинами важно установить отношение логического рассуждения: которое из признаков является причиной, а какое следствием. Например, доходность банковского учреждения зависит от размера ставки по кредитам (депозитам), а не наоборот, то есть экономическая оценка процентной ставки является независимой переменной, а доходность — зависимой. [4]
Следует иметь в виду, что статистический анализ зависимостей сам по себе не раскрывает сущности причинных связей между явлениями, то есть он не решает вопрос, по каким причинам одна переменная влияет на другую. Решение такой задачи является результатом качественного (содержательного) изучения связей, обязательно должен либо предшествовать статистическому анализу или сопровождать его.
Применение методов математического аппарата для эконометрических моделей на различных уровнях экономической деятельности позволяет решать экономические проблемы разного уровня сложности. На уровне макроэкономики математическими средствами эконометрики исследуют закономерности в производстве, распределении, перераспределении и конечном использовании валового внутреннего продукта, в которых существенную роль играют государственный бюджет, налоговая политика, страхование, кредит, сберегательное дело. Согласованность всех отраслей финансово-кредитной системы определяет эффективность распределительных отношений, сбалансированность доходов и расходов в народном хозяйстве, обеспечение процессов воспроизводства денежных ресурсов, финансовой защищенности государственного, коллективного и личного имущества от инфляции и других негативных явлений. На микроуровне эконометрические исследования предполагают научное обоснование управленческих решений, принимаемых на предприятиях различных форм собственности и должны учитывать постоянное воздействие внешней среды.
Модели могут использоваться для анализа экономических и социально-экономических показателей, характеризующих соответствующую экономическую систему, для прогнозирования их дальнейшего изменения или для имитации возможных сценариев социально-экономического развития исследуемой системы при условии, что некоторые показатели можно изменять целенаправленно.
Особое значение эконометрические исследования приобретают в макроэкономике, где взаимосвязи величин часто неочевидные и изменчивы. Не исключены ситуации, когда модель вдруг перестает «работать» из-за появления или активизации какого-нибудь фактора. Именно такие ситуации вызывают развитие макроэкономической теории. С другой стороны, именно эконометрический анализ позволяет обосновать и уточнить форму зависимостей в макроэкономических моделях, лучше понять механизмы взаимосвязи макроэкономических показателей. [3]
Итак, сочетая в себе экономическую теорию и математико-статистические методы, эконометрическое моделирование широко применяется при принятии практических решений в экономической деятельности (в бизнесе, банковском деле, прогнозировании, государственном регулировании экономики), а также является мощной базой для получения новых знаний по экономике.
4. Специфичность применения математических методов в эконометрике.
Термин «эконометрика» означает измерения в экономике, но не все прикладные исследования экономики средствами математики относятся к эконометрии. Эконометрика изучает модели и методы количественной оценки параметров моделей, характеризующих взаимосвязи между экономическими показателями на макро и микро уровне экономики. Именно поэтому процесс изучения экономических явлений и процессов методами эконометрики называется эконометрическим моделированием.
В эконометрике любой результат хозяйственной деятельности на макро и микро уровне экономики рассматривается как очень сложная функция, как по аналитической форме, так и по неопределенно большому количеству условий-факторов. Общий ее вид такой:
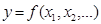 (1)
(1)
где у — зависимая переменная (результат);
xi — независимые переменные (факторы), влияющие на уровень и вариацию y.
Такой сложный объект моделирования объективно невозможно аналитически аппроксимировать однозначным (детерминированным) уравнением. В эконометрическую модель не могут быть включены все условия-факторы, потому что:
- много условий-факторов аналитику неизвестны;
- часть факторов не имеют количественного измерения;
- о некоторых факторах отсутствует информация;
- влияние многих факторов очень незначительно и его можно оставить без внимания.
В эконометрическую модель включается ограниченное количество наиболее важных факторов, и она приобретает вид:
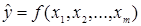 (2)
(2)
где 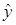 — математическое ожидание, или наиболее вероятное, среднее из возможных значений у.
— математическое ожидание, или наиболее вероятное, среднее из возможных значений у.
Такое упрощение действительности обусловливает возникновение ошибки аппроксимации, или прогноза, потому что в таком случае
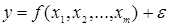 (3)
(3)
где 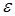 — случайная составляющая у, что объясняется влиянием других (не учтенных и неизвестных) факторов. [7]
— случайная составляющая у, что объясняется влиянием других (не учтенных и неизвестных) факторов. [7]
Это означает, что эконометрические модели является стохастическими, вероятностными. Стохастические зависимости в эконометрике называются также корреляционными. Термин «корреляция» (лат. correlatіo) ввел в научной терминологии английский ученый Ф. Гальтон в 1877. Этот термин буквально означает соотношение, пропорции, связь, зависимость. [2] Для определения зависимостей в эконометрии используются такие обозначения: у — зависимая (эндогенная) переменная; xi — независимые (экзогенные), объясняющие переменные, или факторы. Уравнение (2) называется уравнением регрессии. Такое название введено английским антропологом К. Пирсоном в начале XX века.
Уравнения регрессии могут иметь линейную:
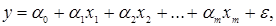
и нелинейную форму, например, степенную:
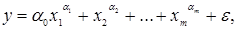
где 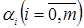 — параметры уравнения регрессии, или коэффициенты регрессии. Они определяют влияние изменение факторов xi на уровень у. [1]
— параметры уравнения регрессии, или коэффициенты регрессии. Они определяют влияние изменение факторов xi на уровень у. [1]
Если модель линейная, то 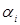 показывает, на сколько единиц изменяется у при изменении xi на единицу. В степенной модели коэффициент регрессии
показывает, на сколько единиц изменяется у при изменении xi на единицу. В степенной модели коэффициент регрессии 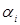 является относительной мерой изменения, он определяет, на сколько процентов изменится у, если xi изменится на один процент. Итак, предметом эконометрии являются методы оценивания параметров уравнений регрессии.
является относительной мерой изменения, он определяет, на сколько процентов изменится у, если xi изменится на один процент. Итак, предметом эконометрии являются методы оценивания параметров уравнений регрессии.
Поскольку независимых переменных в действительности может быить неопределенно много и истинная аналитическая форма зависимостей у от xi неизвестна, коэффициенты регрессии 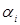 и величину
и величину 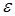 определить однозначно объективно невозможно. Оценивание параметров модели сводится к определению их эмпирических, вероятностных оценок, согласно
определить однозначно объективно невозможно. Оценивание параметров модели сводится к определению их эмпирических, вероятностных оценок, согласно 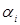 и е. Тогда, например уравнение линейной регрессии приобретает такой вид:
и е. Тогда, например уравнение линейной регрессии приобретает такой вид: 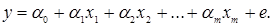
В процессе эконометрического моделирования решаются в общем две проблемы:
1) построение уравнения регрессии, то есть зависимости зависимой (эндогенной) переменной в от независимых (экзогенных) переменных 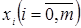 ;
;
2) определение доверительных границ для математического ожидания y, в пределах которых находится случайная составляющая 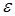 , которая означает ошибку прогноза или аппроксимации y. [3]
, которая означает ошибку прогноза или аппроксимации y. [3]
Решение первой проблемы осуществляется путем решения ряда задач, а именно: идентификация переменных, спецификация аналитической формы уравнения регрессии, оценки параметров уравнения регрессии и его качества. Идентификация, то есть обоснование выбора независимых переменных сначала основывается на предварительном теоретическом, качественном анализе экономической сущности моделируемой зависимости. Затем предварительный перечень независимых переменных должен подвергаться количественной оценке силы и автономности влияния их на зависимую переменную и только после этого можно определить окончательный состав независимых переменных. Для понимания смысла и целей идентификации вводится понятие коэффициента детерминации d. Он определяет удельный вес вариации (колебания) зависимой переменной y под влиянием независимой переменной xi в общей изменчивости зависимой переменной под влиянием совершенно всех независимых переменных. [5]
Спецификация аналитической формы уравнения регрессии заключается в обосновании линейной или определенного вида нелинейной формы зависимостей y от xi. Она сводится к выбору наиболее адекватного теоретической гипотезе аналитика типа из известных в математике уравнений (линейное, параболическое, гиперболическое степенное, экспоненциальное). Оценивание параметров уравнения регрессии — очень сложная и трудоемкая задача моделирования. Это обусловлено особенностями массивов экономической информации о развитии экономических объектов.
Решение второй проблемы эконометрического моделирования состоит в определении доверительных границ для оценки 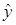 , в пределах которых находится истинное значение y, или ошибка аппроксимации е, то есть разница
, в пределах которых находится истинное значение y, или ошибка аппроксимации е, то есть разница 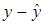 (обозначают
(обозначают 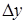 ). [4]
). [4]
Следовательно, решение проблем эконометрического моделирования путем последовательного решения ряда прикладных задач должно привести к получению эконометрической модели в виде: 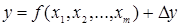
Методы эконометрики являются самыми современными средствами анализа и исследования различных социально-экономических систем. С помощью эконометрических методов можно отклонить некоторые экономические гипотезы или показать невозможность применения в конкретных условиях. Хотя средства эконометрики не позволяют доказать теоретические утверждения, но за счет ее методов можно показать, что то или иное утверждение не противоречит данным наблюдений. Овладев элементарным инструментарием эконометрики, можно обоснованно прогнозировать развитие этих систем, оценивать влияние решений или правительственных постановлений об изменении цен, налогов и т. д. на положение дел любого предприятия, разрабатывать пути эффективного управления ими, принимать эффективные управленческие решения.
Если результаты экономической теории имеют качественное содержание, то эконометрия привносит в них эмпирическую суть. Если математическая экономика выражает экономические законы в виде математических соотношений, то эконометрика осуществляет статистическую проверку этих законов, используя эмпирическую информацию. Полученные математическими методами и выражены языком математики результаты только тогда имеют ценность, если их можно интерпретировать языком экономики.
Эконометрика использует традиционные математико-статистические и специально разработанные методы для выявления количественных взаимосвязей между экономическими показателями. Эконометрика имеет экономическую и математическую составляющие, причем экономическая составляющая является предпочтительней. Изучение эконометрики предполагает соответствующую математическую и экономическую подготовку. Однако для того, чтобы ознакомиться с проблемами, которые изучает эконометрика и с которыми сталкиваются те, кто использует эконометрические методы, не нужно быть специалистом по всем разделам математики и экономики. Знание определенных разделов математики, в частности основ линейной алгебры, теории матриц, теории вероятностей, математической статистики и основ экономики, могут оказаться достаточными для изучения эконометрики.
Литература:
1. Бардасов С. А. Эконометрика: Учебное пособие.-2-е изд., доп. — Тюмень: Издательство ТюмГУ, 2010. — 282 с.
2. Буравлев А. И. Эконометрика Учебное пособие — М.: БИНОМ. Лаборатория знаний, 2012. — 164 с.
3. Гладилин А. В. Эконометрика: учебник / А. В. Гладилин, А. Н. Герасимов, Е. И. Громов. — Ростов н/Д: Феникс, 2011. — 297 с.
4. Елисеева И.И Эконометрика: учебник для магистров — М.: Издательство Юрайт, 2012. — 453 с.
5. Костюнин, В. И. Эконометрика: учебник и практикум для прикладного бакалаврата / В. И. Костюнин. — М.: Издательство Юрайт, 2014. — 285 с.
6. Новиков А. И. Эконометрика Издательство: Дашков и К, 2013 г., — 224 с.
7. Тимофеев, В. С. Эконометрика: учебник для бакалавров / В. С. Тимофеев, А. В. Фадеенков, В. Ю. Щеколдин. — 2-е изд., перераб. и доп. — М.: Издательство Юрайт, 2013. — 328 с.
8. Тихомиров Н. П. Дорохина Е. Ю. Эконометрика: Учебник. — 2-е изд., стереотип. (Серия: 'Учебник Плехановской академии'), 2007. — 512 с.
Ключевые слова
анализ, управление, эффективность, управление., экономика, математические методы, эконометрикаПохожие статьи
Профессиональная подготовка студентов экономических...
экономическая теория, переменная, эконометрика, эконометрическое моделирование, математическая статистика, показатель, модель, Нобелевская премия, математическая экономика, статистическая зависимость.
экономическая теория, переменная, эконометрика...
экономическая теория, переменная, эконометрика, эконометрическое моделирование, математическая статистика, показатель, модель, Нобелевская премия, математическая экономика, статистическая зависимость.
Теоретический обзор эконометрических моделей исследования...
Выделяют два основных направления построения эконометрических моделей реальных национальных экономик
1) модели, в которых анализируются только предыдущие временные значения экономического показателя без учета влияния экзогенных переменных...
Построение эконометрической модели для прогнозирования...
Бывшев В. А. Эконометрика: учебное пособие /В. А. Бывшев. — М.: Финансы и статистика, 2008.
Например, предлагается построить многофакторные эконометрические зависимости и сделать прогноз важных экономических показателей, характеризующих экономику РФ или...
Математическое моделирование комплексных экономических...
математическое моделирование, модель, моделирование, этап, экономическая модель, экономическая теория, процесс, математическая модель, экономическая сфера, мой взгляд.
Эконометрическое моделирование и прогнозирование...
Эконометрическое моделирование и прогнозирование макроэкономических показателей внешней торговли.
Кроме этого, был проведен анализ остаточных величин каждой модели, который продемонстрировал нулевое значение математического ожидания остатков...
Практические приёмы моделирования экономических систем
Эконометрические модели, иначе — экономико-математические модели факторного анализа
Цель построение эконометрических моделей — анализ и прогнозирование конкретных экономических процессов на основе реальной статистической информации.
Использование языка R для эконометрического моделирования...
Сегодня эконометрика является важной частью экономической теории. Пришло понимание того, что без построения эконометрических моделей невозможно проводить современный
Взаимосвязь между переменными величинами может быть описана разными способами.
Актуальные экономико-математические методы исследования...
Экономико-математическая модель (ЭММ) — это математическое описание экономического объекта или процесса с целью их исследования и управления ими.
Бабешко Л. О. Основы эконометрического моделирования: Учеб. пособие.
Похожие статьи
Профессиональная подготовка студентов экономических...
экономическая теория, переменная, эконометрика, эконометрическое моделирование, математическая статистика, показатель, модель, Нобелевская премия, математическая экономика, статистическая зависимость.
экономическая теория, переменная, эконометрика...
экономическая теория, переменная, эконометрика, эконометрическое моделирование, математическая статистика, показатель, модель, Нобелевская премия, математическая экономика, статистическая зависимость.
Теоретический обзор эконометрических моделей исследования...
Выделяют два основных направления построения эконометрических моделей реальных национальных экономик
1) модели, в которых анализируются только предыдущие временные значения экономического показателя без учета влияния экзогенных переменных...
Построение эконометрической модели для прогнозирования...
Бывшев В. А. Эконометрика: учебное пособие /В. А. Бывшев. — М.: Финансы и статистика, 2008.
Например, предлагается построить многофакторные эконометрические зависимости и сделать прогноз важных экономических показателей, характеризующих экономику РФ или...
Математическое моделирование комплексных экономических...
математическое моделирование, модель, моделирование, этап, экономическая модель, экономическая теория, процесс, математическая модель, экономическая сфера, мой взгляд.
Эконометрическое моделирование и прогнозирование...
Эконометрическое моделирование и прогнозирование макроэкономических показателей внешней торговли.
Кроме этого, был проведен анализ остаточных величин каждой модели, который продемонстрировал нулевое значение математического ожидания остатков...
Практические приёмы моделирования экономических систем
Эконометрические модели, иначе — экономико-математические модели факторного анализа
Цель построение эконометрических моделей — анализ и прогнозирование конкретных экономических процессов на основе реальной статистической информации.
Использование языка R для эконометрического моделирования...
Сегодня эконометрика является важной частью экономической теории. Пришло понимание того, что без построения эконометрических моделей невозможно проводить современный
Взаимосвязь между переменными величинами может быть описана разными способами.
Актуальные экономико-математические методы исследования...
Экономико-математическая модель (ЭММ) — это математическое описание экономического объекта или процесса с целью их исследования и управления ими.
Бабешко Л. О. Основы эконометрического моделирования: Учеб. пособие.







