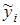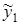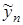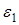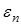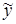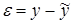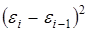В настоящее время студенты, обучающиеся по направлению «Экономика» и «Менеджмент» начали изучать новую дисциплину — «Эконометрика». Данная дисциплина относится к профессиональному модулю, способствует формированию умений на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты.
Успешность изучения курса «Эконометрика» во многом зависит от уровня освоения таких смежных дисциплин, как экономическая теория, математическая экономика, экономическая статистика, математическая статистика и теория вероятностей. Эконометрические методы в России мало известны. Поэтому возникают трудности, заключающиеся в недостаточном количестве учебной литературы, способствующей формированию у студентов навыков практического применения теоретических основ эконометрического моделирования. Для решения указанных выше задач при изучении курса «Эконометрика» используются лекционная и лабораторная формы занятий.
Курс лекций делится на два блока. Основной целью лекций, составляющих первый блок, является повторение основных теоретических сведений из математической статистики и теории вероятностей. Лекции, составляющие второй блок, ориентированы на овладение: терминологией, методологическими основами эконометрического моделирования. Целью лабораторных работ является овладение студентами методами статистического анализа конкретных экономических данных. Задания лабораторных работ выполняются с привлечением возможностей MS Excel.
Рассмотрим практические рекомендации по выполнению расчетов с помощью табличного редактора MS Excel.
Представлены данные о доходах по акциям x и балансовой прибыли y по 11 предприятиям одной отрасли, ден. ед.
|
x |
3 |
4 |
5 |
7 |
8 |
10 |
11 |
12 |
15 |
20 |
30 |
|
y |
12 |
13 |
20 |
19 |
31 |
24 |
41 |
28 |
52 |
55 |
103 |
Задание. Проверить выполнение следующих требований:
1. Уровни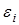 
ряда остатков имеют случайный характер.
2. Математическое ожидание уровней ряда остатков равно нулю.
3. Значения 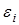независимы друг от друга, т. е. отсутствует автокорреляция.
1. Для проверки случайности ряда остатков можно использовать критерий поворотных точек (пиков). Предварительно составляют таблицу данных:
|
|
|
… |
|
|
|
|
… |
|
Точка 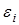считается поворотной, если выполняются следующие условия
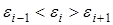или 
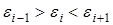. (1)
Далее подсчитывается число поворотных точек p. Критерием случайности с 5 %-ным уровнем значимости, т. е. с доверительной вероятностью 95 %, является выполнение равенства
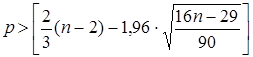, (2)
где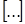 
– целая часть числа. Если неравенство выполняется, то модель считается адекватной.
Пусть расчет регрессии дал следующие результаты
,
|
|
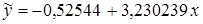x |
y |
|
Остатки |
|
|
3 |
12 |
9,165277 |
2,834723 |
|
|
4 |
13 |
12,39552 |
0,604484 |
|
|
5 |
20 |
15,62576 |
4,374245 |
|
|
7 |
19 |
22,08623 |
-3,086233 |
|
|
8 |
31 |
25,31647 |
5,683528 |
|
|
10 |
24 |
31,77695 |
-7,77695 |
|
|
11 |
41 |
35,00719 |
5,992811 |
|
|
12 |
28 |
38,23743 |
-10,237428 |
|
|
15 |
52 |
47,92815 |
4,071855 |
|
|
20 |
55 |
64,07934 |
-9,07934 |
|
|
30 |
103 |
96,38173 |
6,61827 |
|
Среднее |
|
|
|
-3,18182E-06 |
Цветом выделены поворотные точки. Их всего 9, в этом легко убедиться, если просмотреть пики графика (значения фактора x должны быть отсортированы по возрастанию)
.
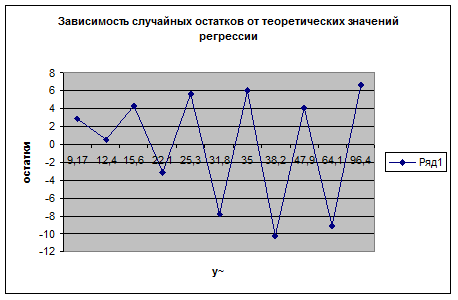
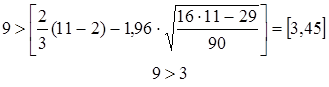Неравенство верное, остатки признаем случайными.
2. Для проверки равенства математического ожидания остаточной последовательности нулю вычисляется среднее значение ряда остатков
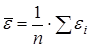. (3)
Если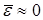 
, то считается, что модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего. Если 
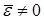, то проверяется гипотеза о равенстве нулю математического ожидания. Для этого вычисляют t-критерий Стъюдента по формуле
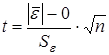, (4)
где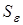 
— среднее квадратическое отклонение ряда остатков, 
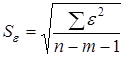, m — число параметров при переменной x.
Значение t-критерия сравнивают с табличным при заданном уровне значимости. Если выполняется неравенство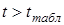 
, то модель неадекватна по данному критерию.
По расчетам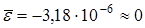 
, то есть по данному пункту модель признаем адекватной.
3. Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществляют с помощью d-критерия Дарбина-Уотсона. Расчетное значение критерия определяется по формуле
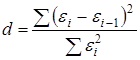(5)
и сравнивается с нижним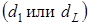 
и верхним 
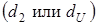критическими значениями статистики Дарбина-Уотсона.
Возможны следующие случаи:
1) Если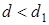 
, то гипотеза о независимости остатков отвергается, и модель признается неадекватной по критерию независимости остатков.
2) Если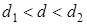 
, включая сами эти значения, то считается, что нет достаточных оснований делать тот или иной вывод.
3) Если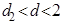 
, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию.
4) Если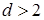 
, то это свидетельствует об отрицательной автокорреляции остатков. В этом случае расчетное значение критерия необходимо преобразовать по формуле 
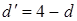и сравнивать с критическим значением не d, а 
.
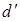Составляем вспомогательную таблицу:
|
|
x |
y |
y~ |
Остатки ε |
|
|
|
|
3 |
12 |
9,165277 |
2,834723 |
|
8,035654 |
|
|
4 |
13 |
12,39552 |
0,604484 |
4,973965997 |
0,365400906 |
|
|
5 |
20 |
15,62576 |
4,374245 |
14,211098 |
19,13401932 |
|
|
7 |
19 |
22,08623 |
-3,086233 |
55,65873199 |
9,52483413 |
|
|
8 |
31 |
25,31647 |
5,683528 |
76,908708 |
32,30249053 |
|
|
10 |
24 |
31,77695 |
-7,77695 |
181,184468 |
60,4809513 |
|
|
11 |
41 |
35,00719 |
5,992811 |
189,606318 |
35,91378368 |
|
|
12 |
28 |
38,23743 |
-10,237428 |
263,420658 |
104,8049321 |
|
|
15 |
52 |
47,92815 |
4,071855 |
204,75558 |
16,58000314 |
|
|
20 |
55 |
64,07934 |
-9,07934 |
172,9539299 |
82,43441484 |
|
|
30 |
103 |
96,38173 |
6,61827 |
246,4149597 |
43,80149779 |
|
Сумма |
|
|
|
|
1410,088418 |
413,3779817 |
Определяем значение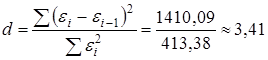 
. Критические значения критерия Дарбина-Уотсона находят по специальным таблицам для заданных объема наблюдений n и числа независимых переменных модели 
.
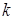В нашем случае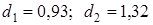 
. Имеем отрицательную автокорреляцию остатков. Переходим к , 
.
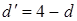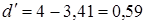Так как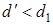 
, модель признается неадекватной, остатки регрессии взаимозависимы. Уравнение регрессии 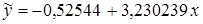не может быть использовано для прогнозирования. Автокорреляция в остатках может иметь разные причины. Возможно, форма связи неточна, или в уравнение не включен какой-либо существенный фактор.
Таким образом, выполнение лабораторных работ способствует повышению уровня освоения учебного материала, так как привлечение возможностей MS Excel позволяет, с одной стороны, «прочувствовать» все детали и тонкости изучаемых методов, а с другой — совершенствовать навыки работы в пакете MS Excel, необходимые для работы экономиста. Тем самым у студентов формируются умения строить математические модели простейших реальных явлений, исследовать явления по заданным моделям, что способствует усилению мотивационной составляющей обучения.
Литература:
1. Куимова К. А., Куимова Е. И., Ячинова С. Н. Профессиональная подготовка экономистов посредством решения оптимизационных задач // Молодой ученый. — 2014. — № 15. — С. 282–286.
2. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах // Молодой ученый. — 2013. — № 12 (59). — С. 3–6.
3. Крымская Ю.А, Титова Е. И., Ячинова С. Н. Профессиональная подготовка строителей через решение математических задач // Современные проблемы науки и образования. — 2014. — № 2. — С.168.
4. Ячинова С. Н., Гудкова В. С. Мотивация обучения студентов посредством моделирования // Молодой ученый. — 2014. — № 4 — С.1141–1144.
