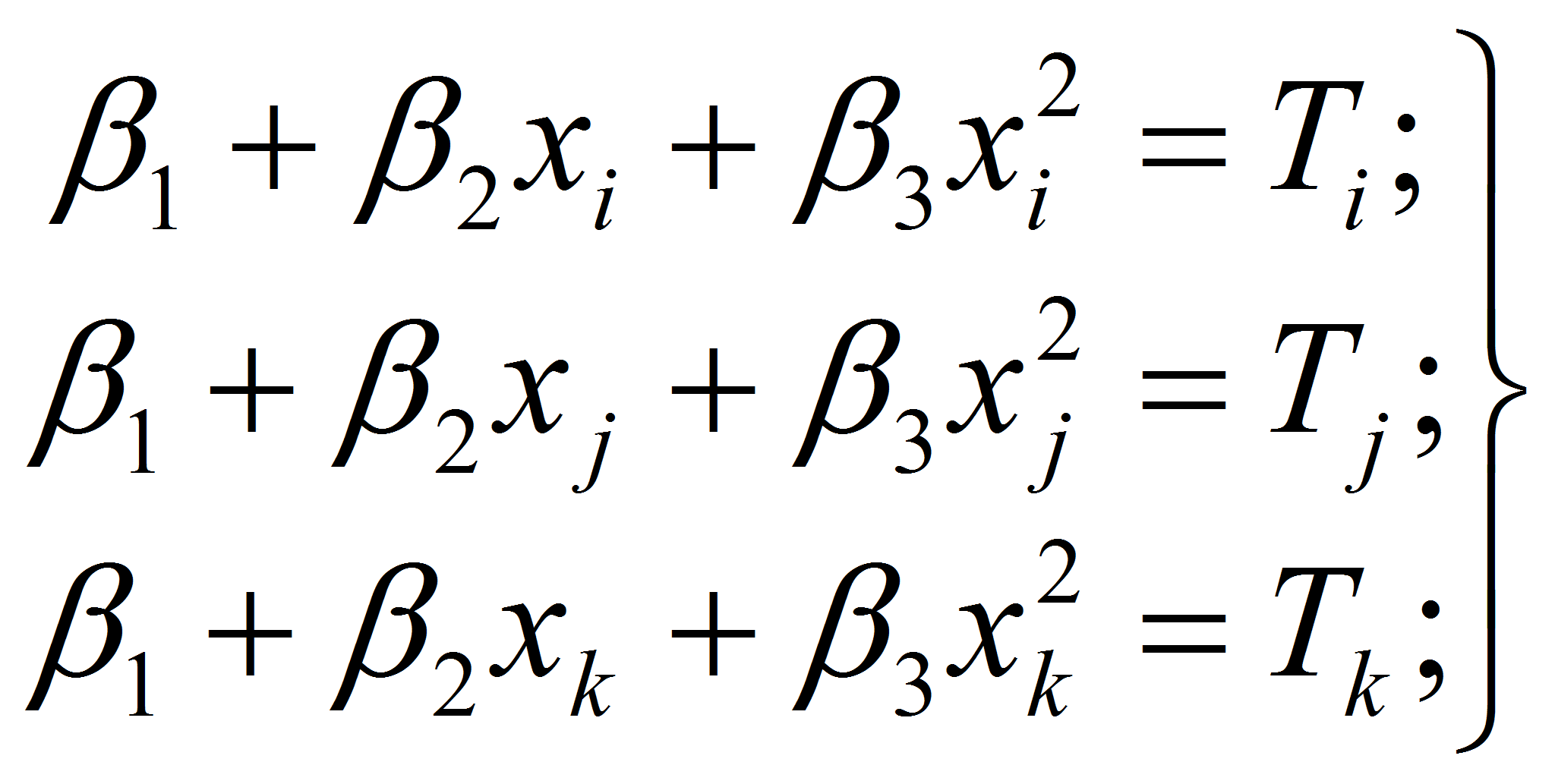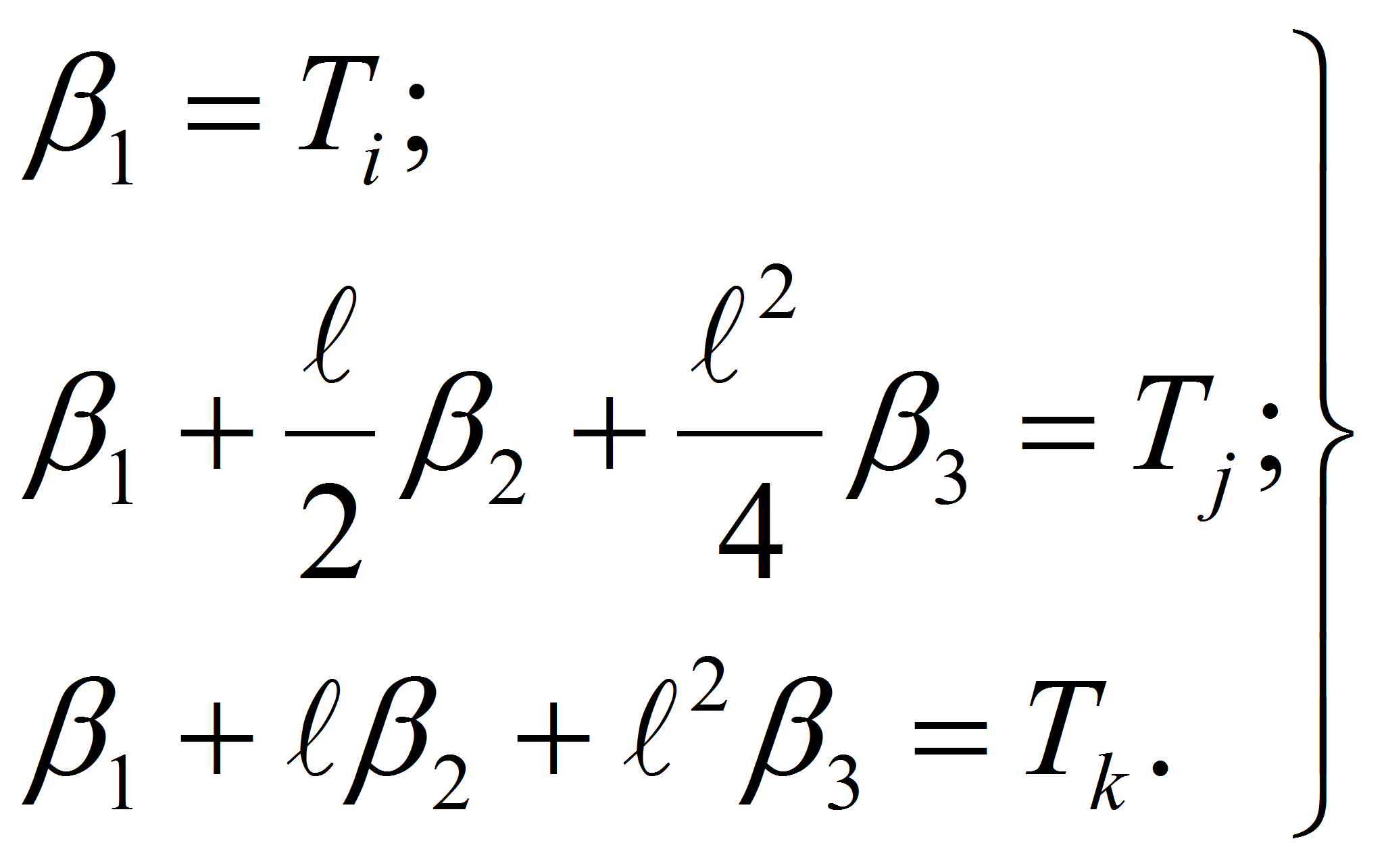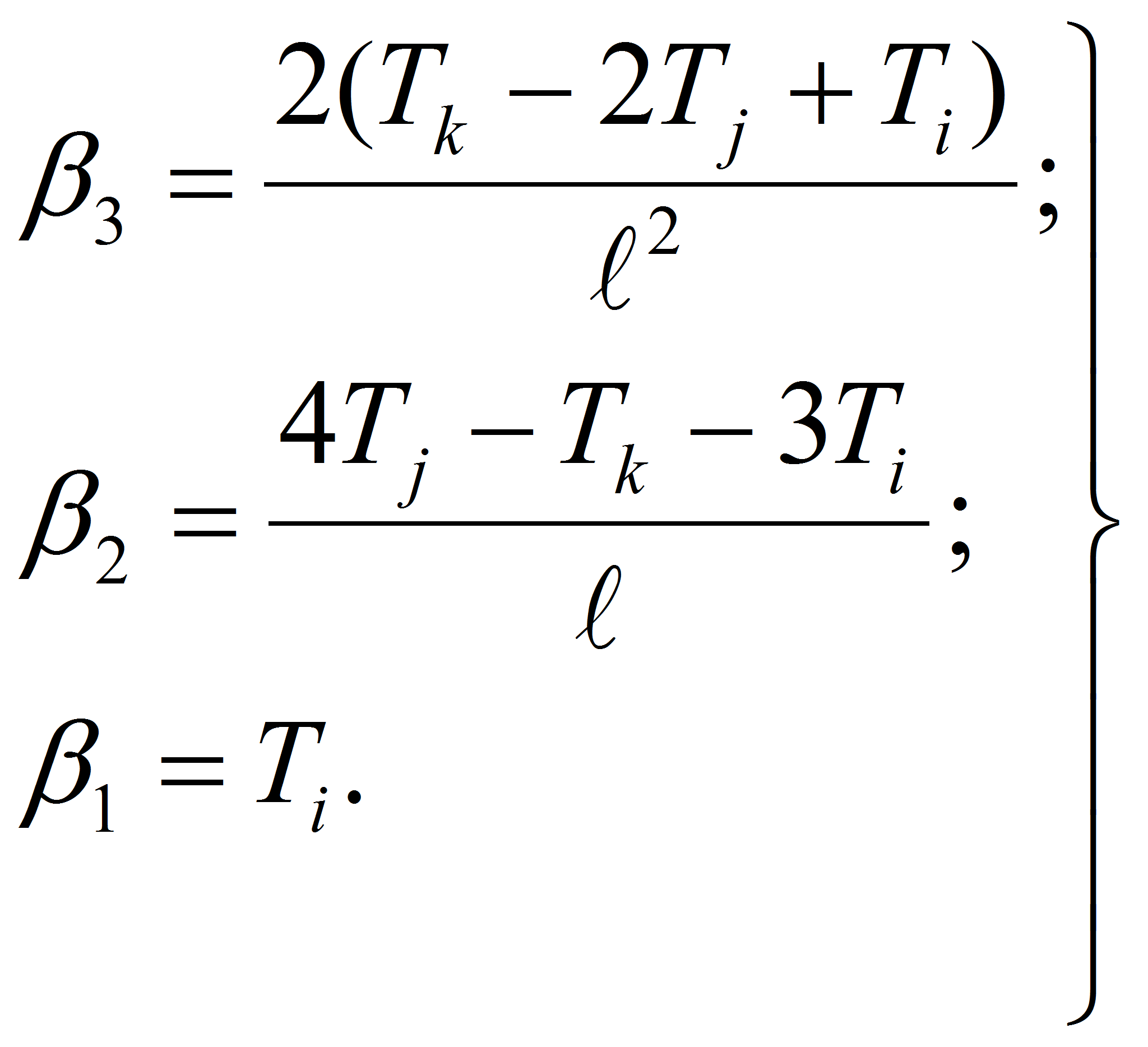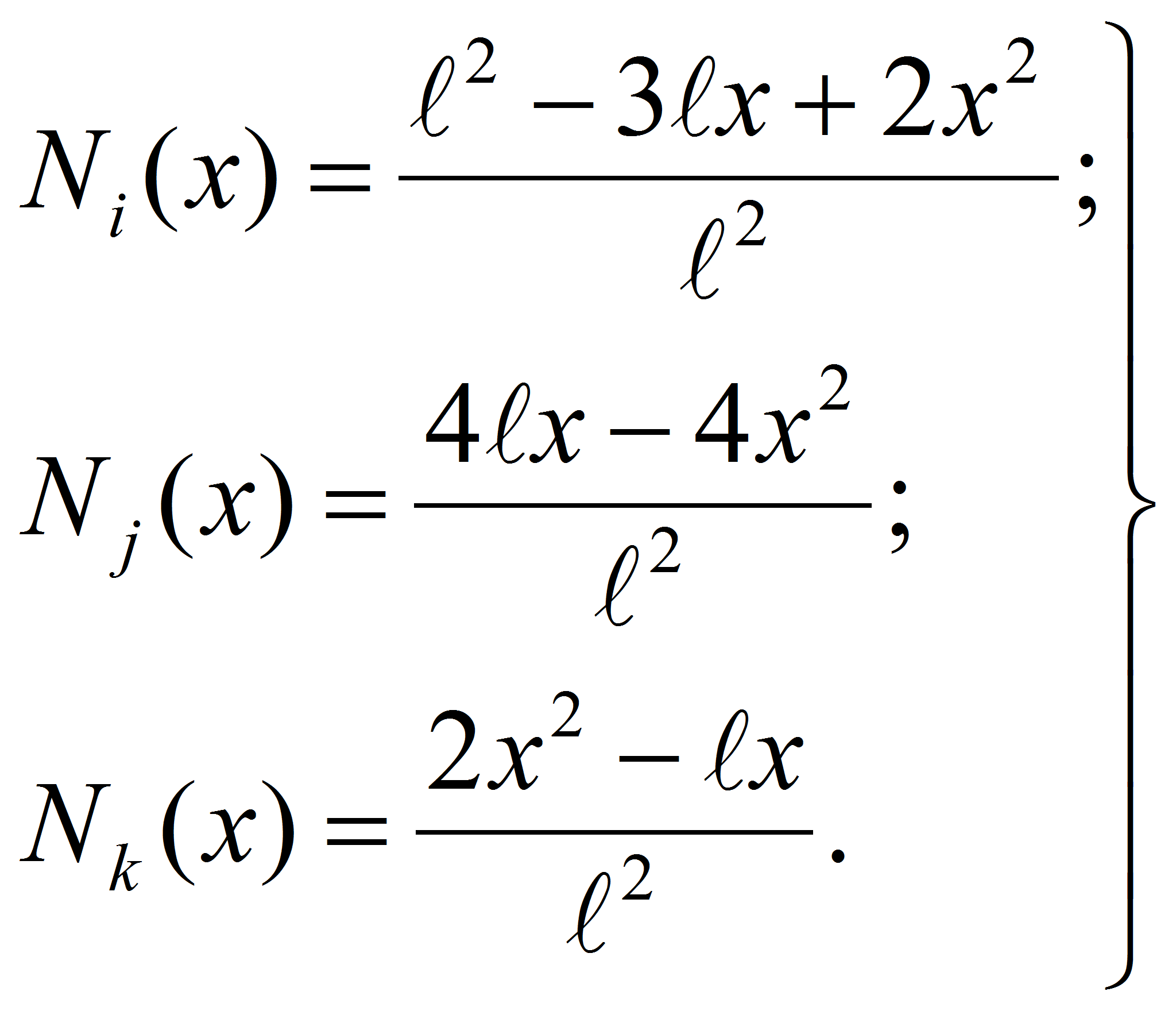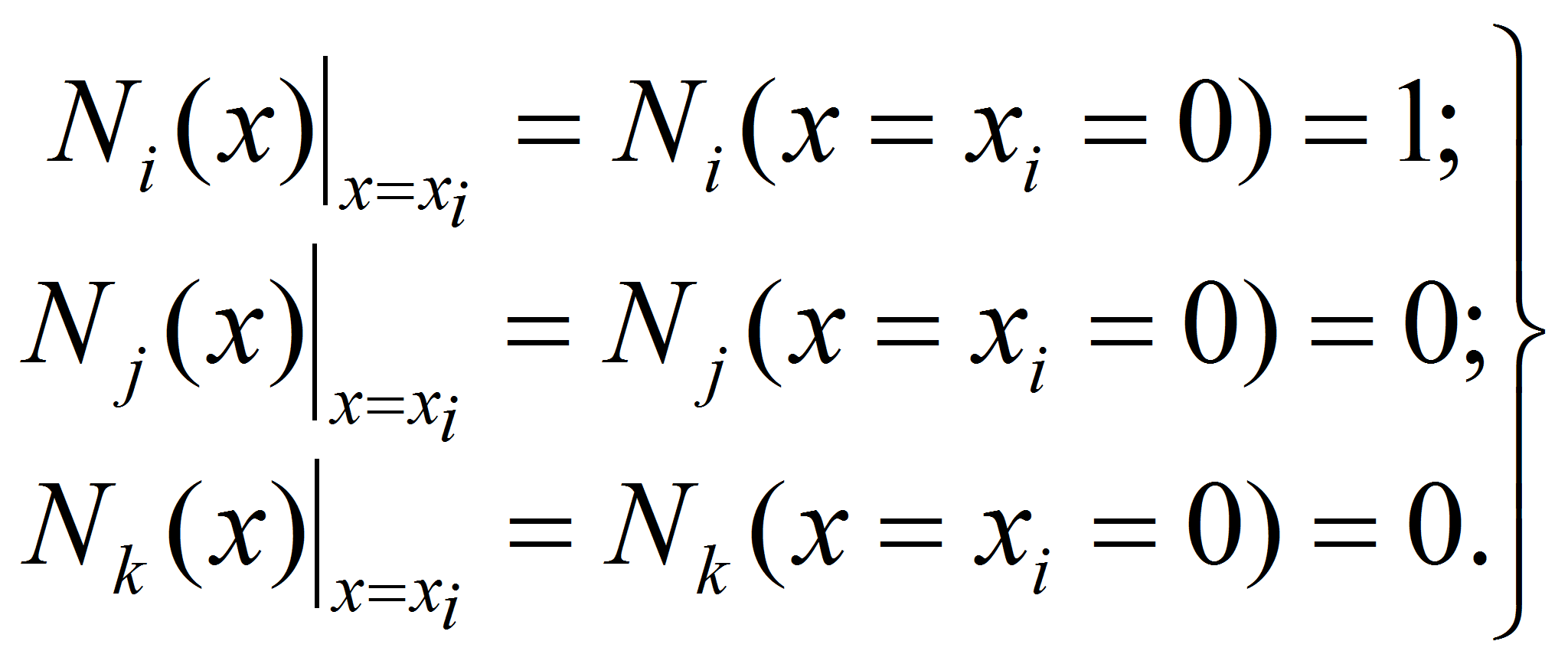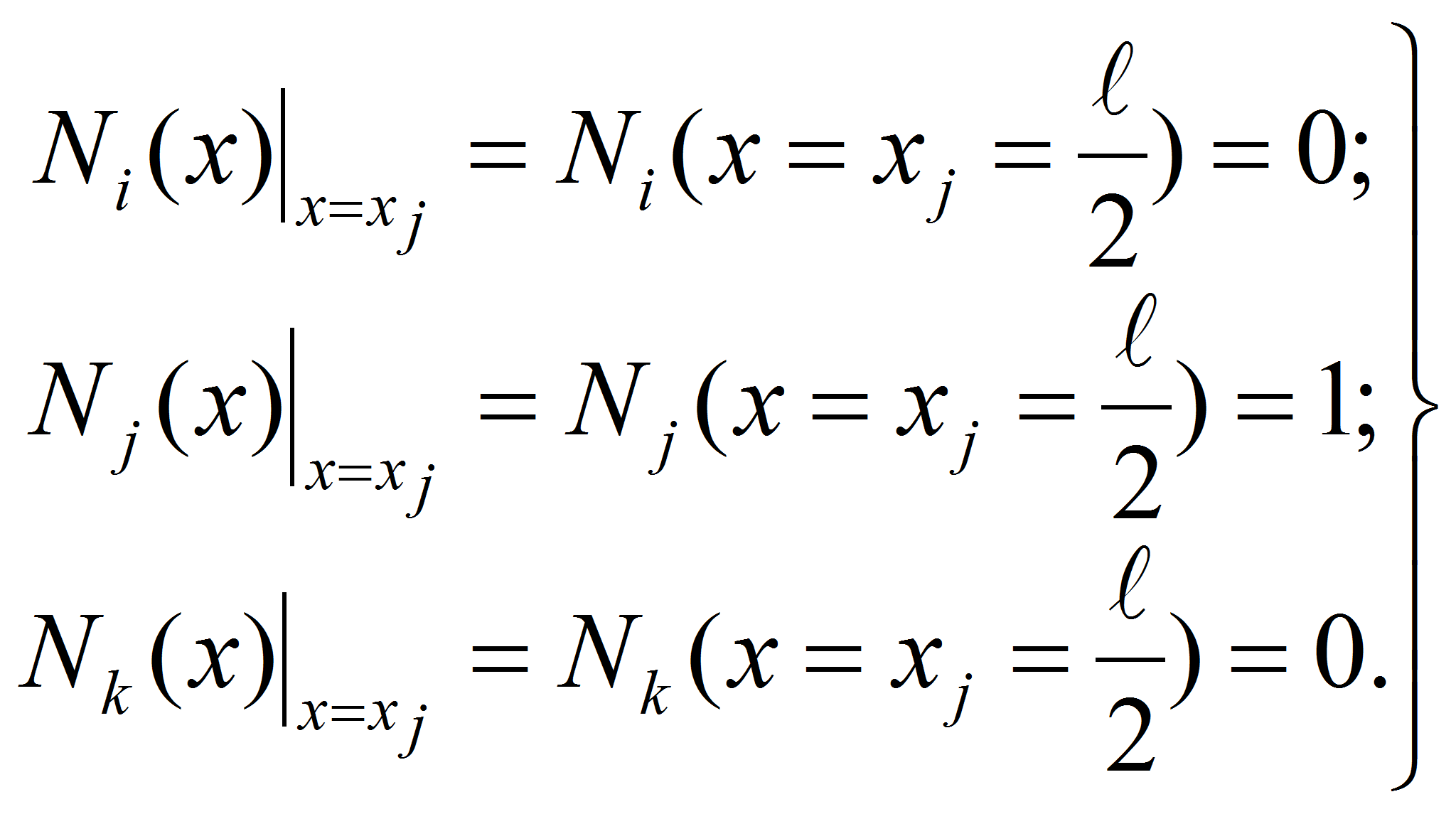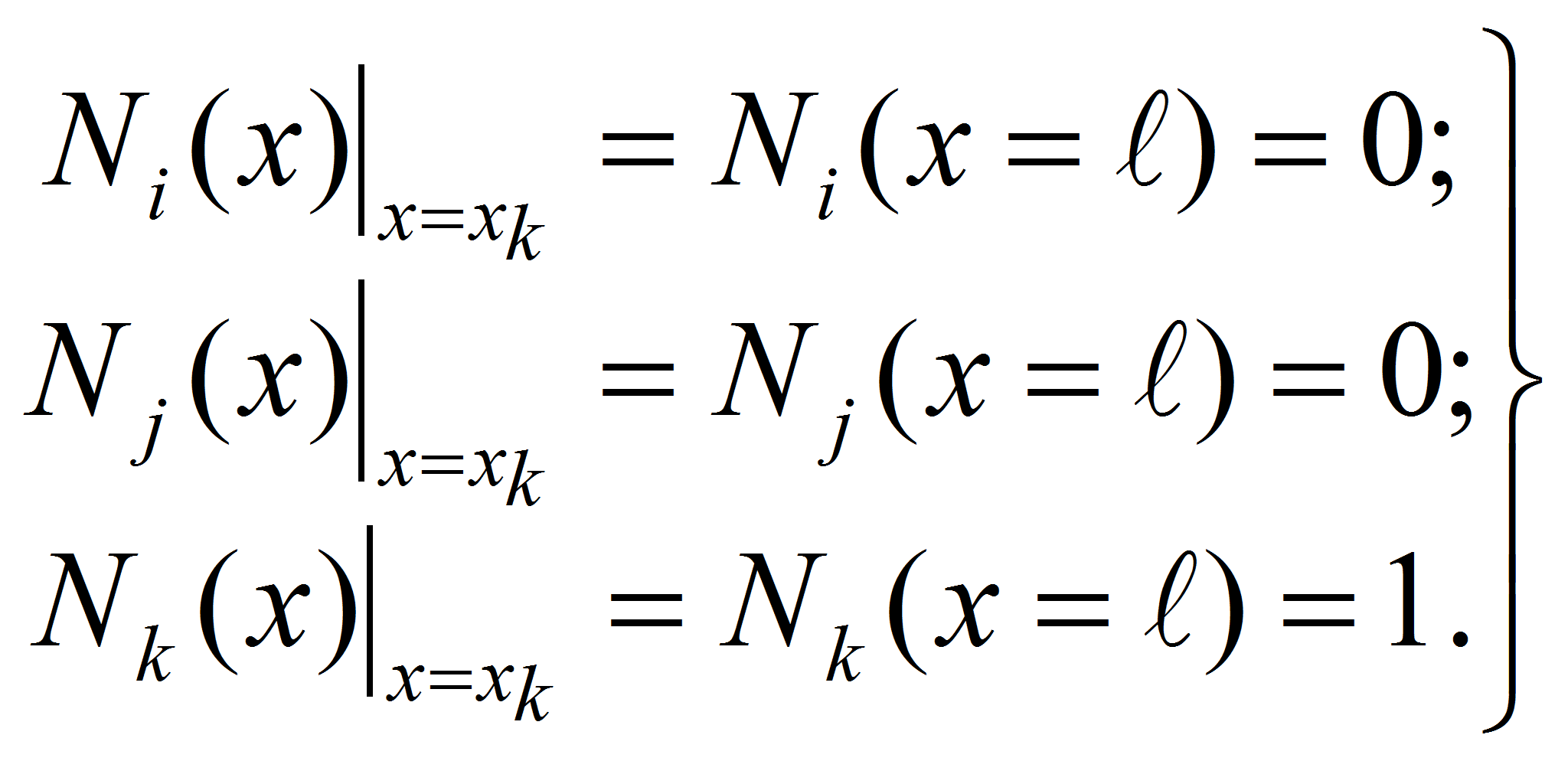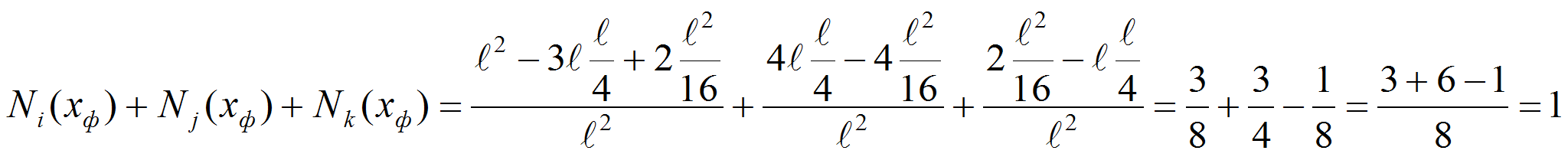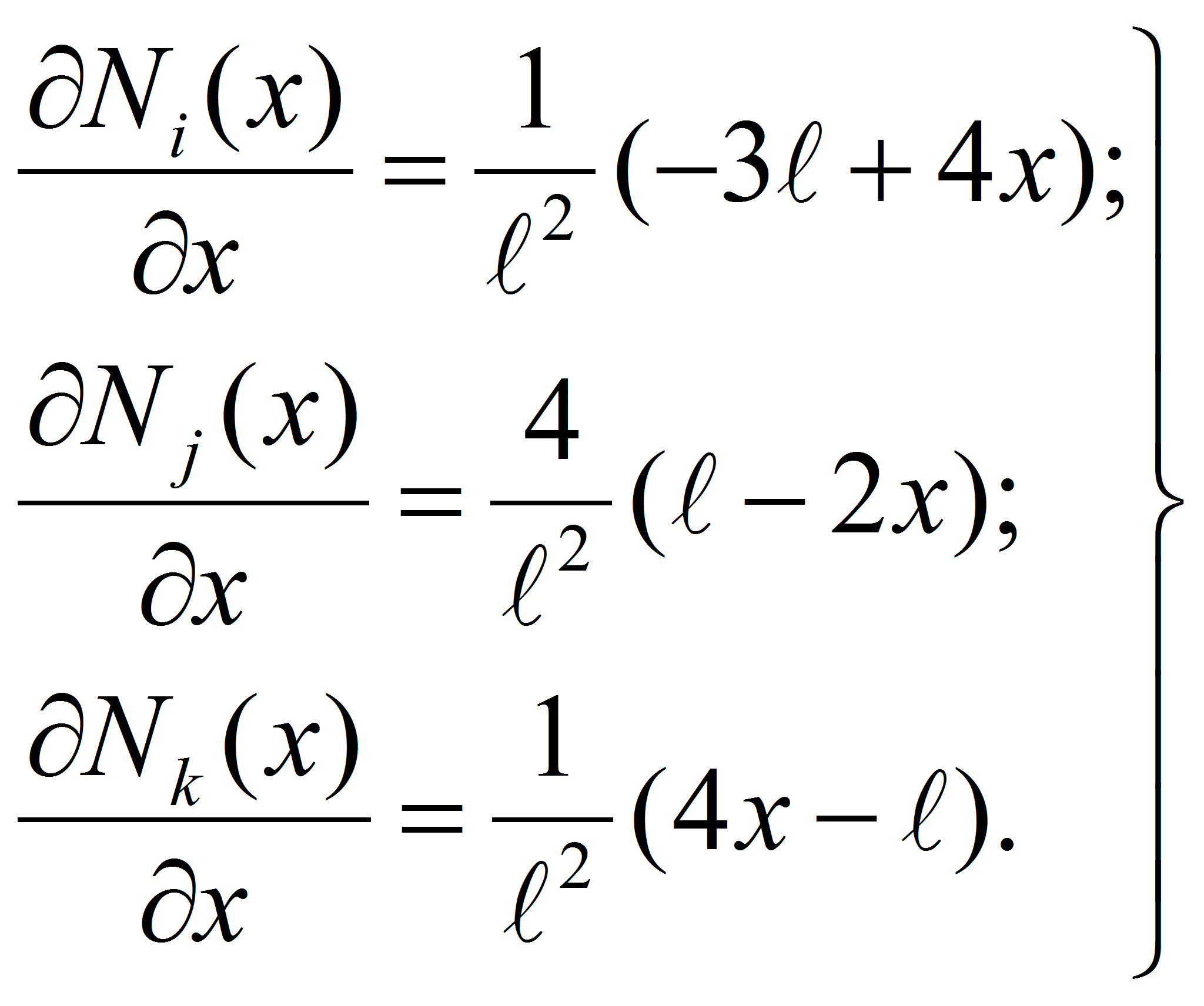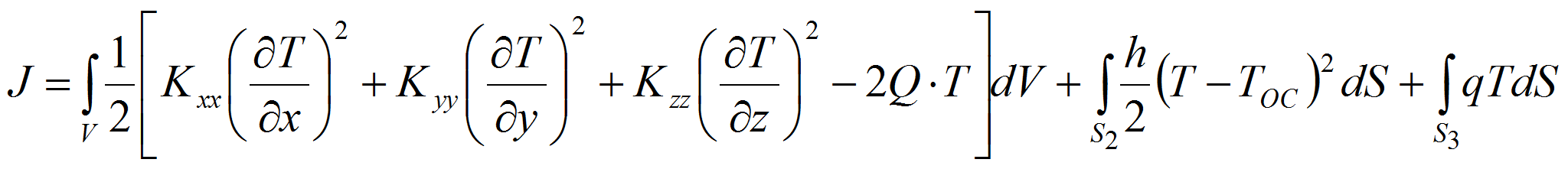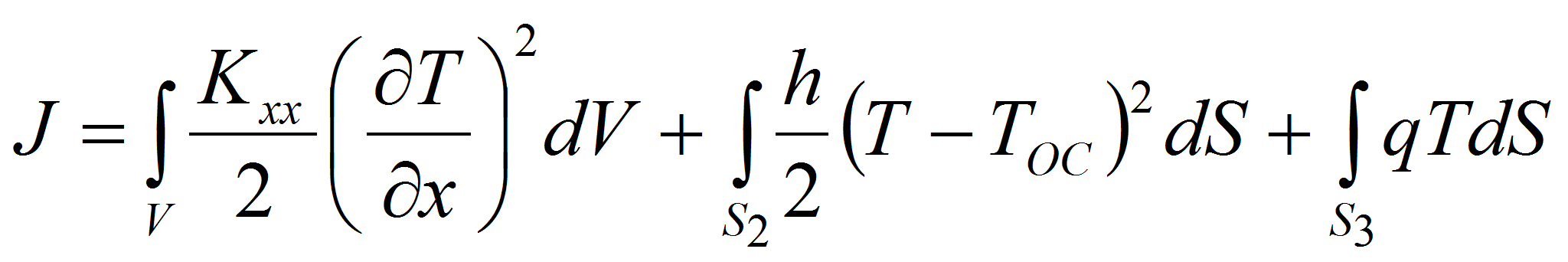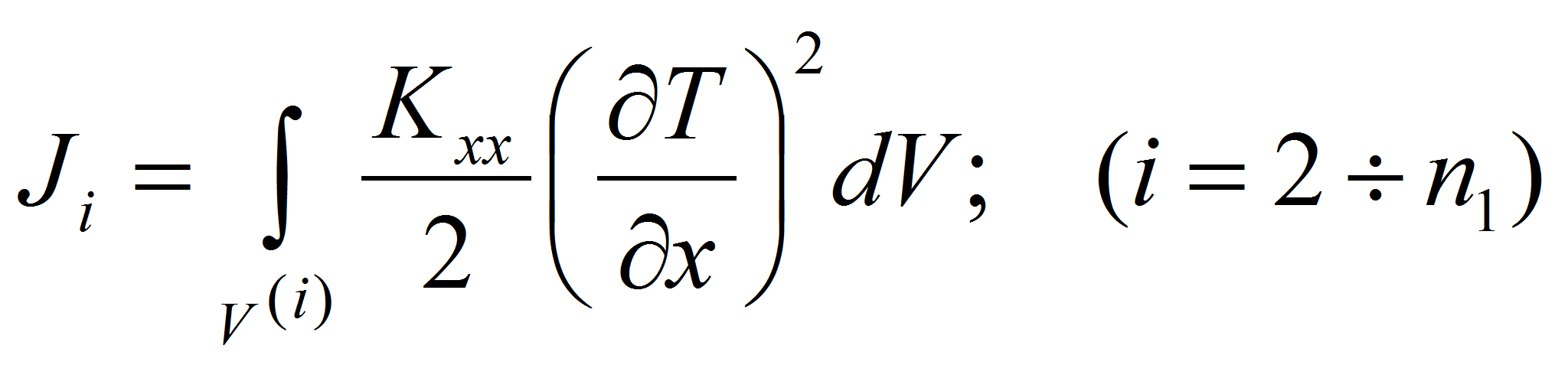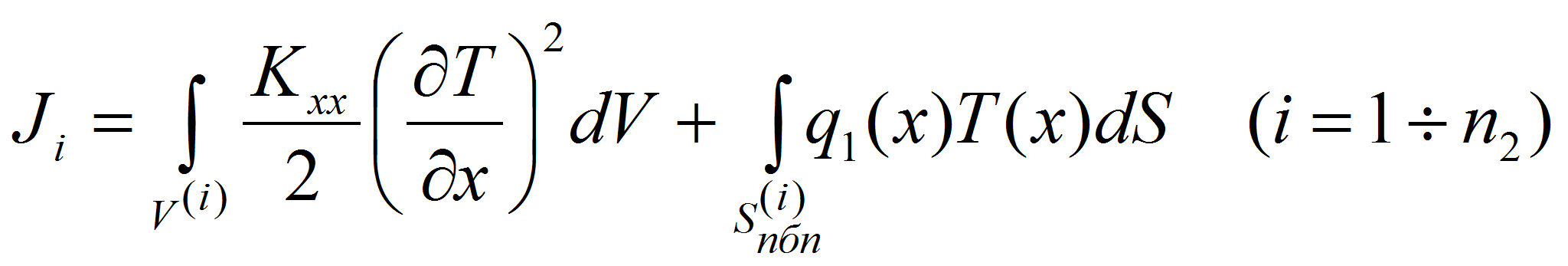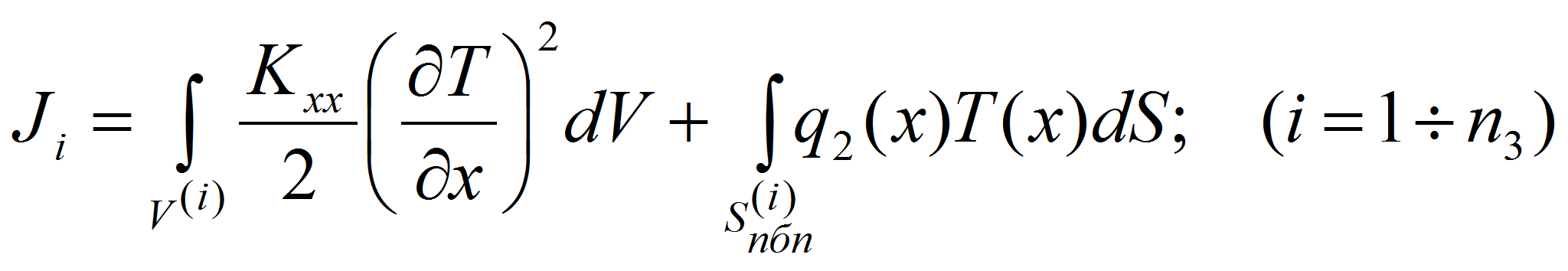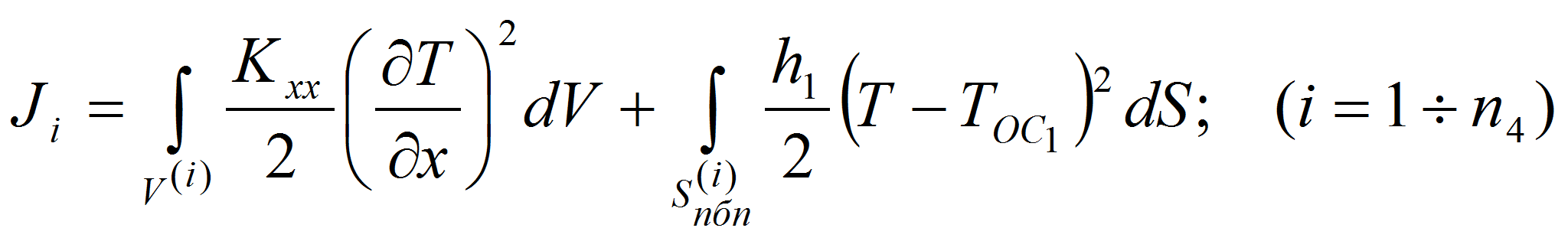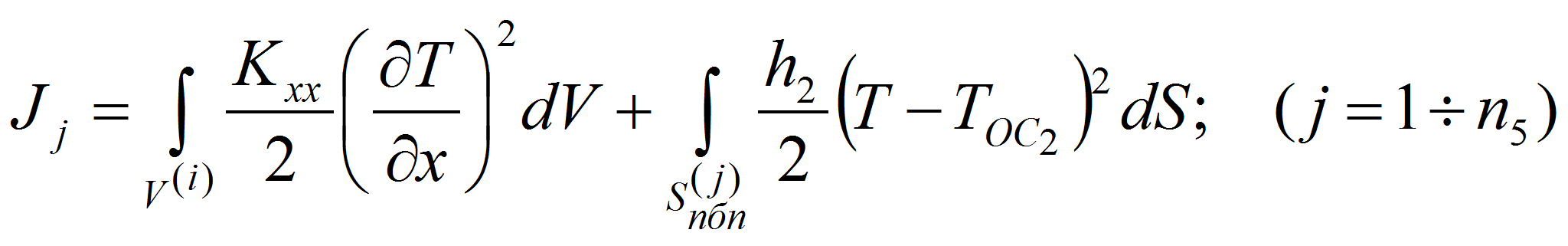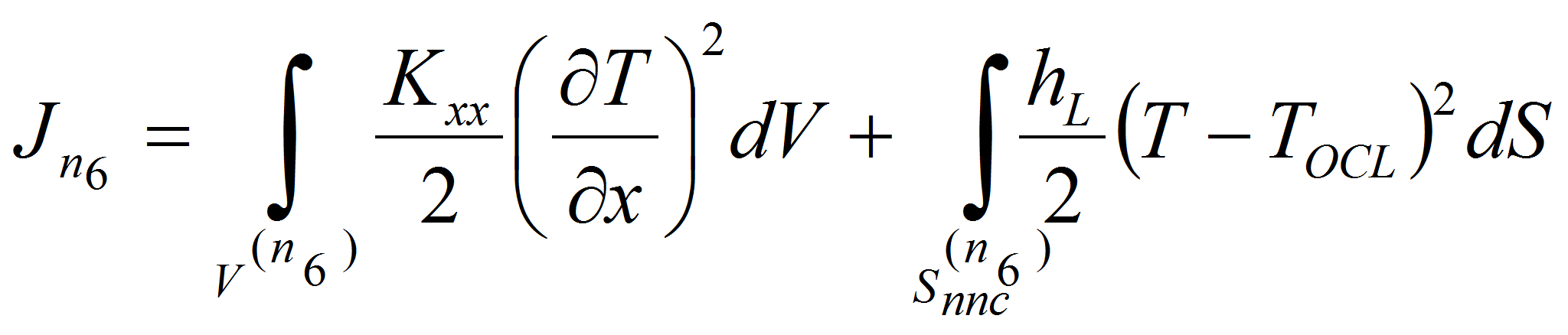Обоснование методики учета температуры при исследованиях и расчетах напряженно-деформированого состояния стержневых элементов проектируемых машин
Авторы: Макатова Валентина Еркиновна, Ахметов Сайранбек Махсутович, Тулеуова Райгуль Орынбасаровна
Рубрика: 7. Машиностроение
Опубликовано в
Статья просмотрена: 135 раз
Библиографическое описание:
Макатова, В. Е. Обоснование методики учета температуры при исследованиях и расчетах напряженно-деформированого состояния стержневых элементов проектируемых машин / В. Е. Макатова, С. М. Ахметов, Р. О. Тулеуова. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы I Междунар. науч. конф. (г. Санкт-Петербург, март 2011 г.). — Санкт-Петербург : Реноме, 2011. — С. 16-23. — URL: https://moluch.ru/conf/tech/archive/2/231/ (дата обращения: 26.04.2024).
При проектировании машин, в частности, при исследованиях и расчетах напряженно-деформированного состояния их составных деталей часто сталкиваемся с задачей учета влияния на общую нагрузку температуры. Такие задачи возникают при проектировании машин, применяемых в металлургической, химической, нефтехимической, пищевой, мясо-молочной и во многих других видах промышленности, где рабочие органы, помимо механической нагрузки, испытывают и температурные напряжения, которые неизбежны в силу принципа и (или) назначения работы этих машин. Например, в нефтегазовой и нефтехимической промышленности: трубчатые элементы машин и аппаратов, через которые протекают жидкости высокой температуры; бурильные трубы нагревающиеся в процессе углубления скважин; насосно-компрессорные трубы, нагревающиеся в силу работы трения насосов. В общем машиностроении, в качестве примера можно привести несущие валы паровых турбин, лопасти, коленчатые валы и системы охлаждения двигателей внутреннего сгорания, рабочие органы тормозных систем (ленты, колодки, диски, шкивы, барабаны) и т.п.
В этой статье приведена методика исследования частично теплоизолированных стержневых элементов, которые в практике являются основными составляющими элементами многих машин и работают под воздействием осевых сил, переменной по координате температуры, теплового потока и теплообмена. При таких сложных воздействиях исследования термоупругого напряженно-деформируемого состояния частично теплоизолированных стержней становится весьма сложной задачей.
Возникающие при таких ситуациях поля температур, перемещения, деформаций и напряжения, как правило, будут распределены по длине стержня нелинейным образом. В связи с этим, для исследования и дальнейших расчетов поле распределения физических величин в малой части длины стержня следует принять в виде кривой второго порядка.
Рассмотрим поле распределения температуры в
интервале
![]() ,
где
,
где
![]() – конечная длина рассматриваемого частично
теплоизолированного стержня;
– конечная длина рассматриваемого частично
теплоизолированного стержня;
![]() -длина
части стержня,
-длина
части стержня,
![]() .
Предположим, что поперечное сечение постоянно по длине стержня, тогда
в интервале
.
Предположим, что поперечное сечение постоянно по длине стержня, тогда
в интервале
![]() ,
поле распределения температуры
,
поле распределения температуры
![]() представим
в виде кривой второго порядка [1, с. 77]
представим
в виде кривой второго порядка [1, с. 77]
где
![]() - некоторые константы, значения которых пока неизвестны. Для
нахождения значения этих констант, рассматриваемую часть стержня
делим пополам. И в этой части фиксируем три узла
- некоторые константы, значения которых пока неизвестны. Для
нахождения значения этих констант, рассматриваемую часть стержня
делим пополам. И в этой части фиксируем три узла
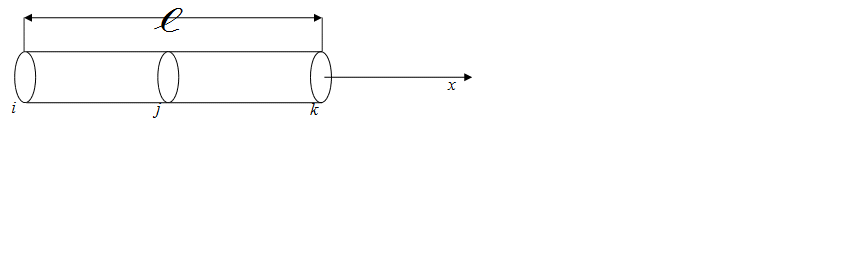
![]() (рис. 1). Глобальные координаты этих узлов соответственно равны
(рис. 1). Глобальные координаты этих узлов соответственно равны
![]()
![]()
![]() ,
при этом
,
при этом
![]() .
.
Рис. 1. Одномерный квадратичный конечный элемент
В местной системе координат координаты трёх узлов определяются
следующим образом:![]()
![]()
![]() .
Введём следующее обозначение, характеризующее значение температуры в
узлах
.
Введём следующее обозначение, характеризующее значение температуры в
узлах
![]() .
.
Решая (1) и (2) совместно получим систему уравнений для определения
значения констант
![]()
учитывая, что
![]() ,
,
![]() ,
,
![]() из последней системы имеем
из последней системы имеем
Учитывая, что
![]() ,
из последних двух уравнений системы (4) получим
,
из последних двух уравнений системы (4) получим
Отсюда определим:
Подставляя найденные значения
![]() в выражение (1) имеем
в выражение (1) имеем
Введём следующее обозначение
Тогда с учётом (8) перепишем (7) в следующем виде
при
![]() .
Функции
.
Функции
![]() называются функциями формы [2, с. 136-141] для одномерного
квадратичного конечного элемента с тремя узлами. Следует отметить,
что эти функции формы имеют определённые свойства. Теперь рассмотрим
свойства этих функций формы в следующих функциях:
называются функциями формы [2, с. 136-141] для одномерного
квадратичного конечного элемента с тремя узлами. Следует отметить,
что эти функции формы имеют определённые свойства. Теперь рассмотрим
свойства этих функций формы в следующих функциях:
Кроме того, для любой точки
![]() в интервале
в интервале
![]() имеет место
имеет место
Например, пусть
![]() .
Тогда получили бы следующий результат
.
Тогда получили бы следующий результат
Также функции формы имеют следующие свойства. Для любой точки
интервала
![]() ,
т.е. в пределах каждого конечного элемента имеет место
,
т.е. в пределах каждого конечного элемента имеет место
Пользуясь соотношениями (8) докажем тождество
Далее находим сумму
Теперь находим значения следующих интегралов, значения которых в последующем будут необходимы:
Кроме того, пользуясь соотношениями
найдем значения следующих интегралов
Как известно значения температурных напряжений в некоторых случаях могут превышать предел прочности элементов конструкций. Поэтому для расчета температурных напряжений в элементах конструкций с начала следует определить закон распределения температуры в исследуемых элементах. Уравнение теплопроводности в сплошной среде имеет вид [3, с. 88]:
где
![]() –
температура, размерность которого
–
температура, размерность которого
![]() ;
;
![]() -
коэффициент теплопроводности (материала тела) в направлениях
-
коэффициент теплопроводности (материала тела) в направлениях
![]() ,
размерности
,
размерности
![]() ;
Q- источник тепла внутри тела, который
считается положительным, если тепло подводится к телу, его
размерность
;
Q- источник тепла внутри тела, который
считается положительным, если тепло подводится к телу, его
размерность
![]() .
Для (16) имеют место следующие граничные условия: если в точках
поверхности
.
Для (16) имеют место следующие граничные условия: если в точках
поверхности
![]() известна температура, то на этой поверхности граничные условия будут
известна температура, то на этой поверхности граничные условия будут
где
![]() – заданная температура на границе, которая может быть
функцией координат точек поверхности
– заданная температура на границе, которая может быть
функцией координат точек поверхности
![]() .
Если через поверхность
.
Если через поверхность
![]() проходит конвективный теплообмен, который характеризуется величиной
проходит конвективный теплообмен, который характеризуется величиной
![]() ,
то для точек этой поверхности граничные условия имеют вид
,
то для точек этой поверхности граничные условия имеют вид
где
![]() - коэффициент теплообмена,
- коэффициент теплообмена,
![]() и этот коэффициент может быть функцией координат точек
поверхности
и этот коэффициент может быть функцией координат точек
поверхности
![]() ;
;
![]() – температура в точках поверхности
– температура в точках поверхности
![]() ,
значение, которого неизвестно;
,
значение, которого неизвестно;
![]() – заданная температура окружающей поверхности
– заданная температура окружающей поверхности
![]() среды. Она тоже может быть функцией координат точек поверхности
среды. Она тоже может быть функцией координат точек поверхности
![]() ;
;
![]() -
направляющие косинусы поверхности
-
направляющие косинусы поверхности
![]() .
Если на поверхность
.
Если на поверхность
![]() тела подведен тепловой поток
тела подведен тепловой поток
![]() ,
,
![]() ,
то для точек этой поверхности имеет место
,
то для точек этой поверхности имеет место
Заданный тепловой поток
![]() может быть функцией координат точек поверхности
может быть функцией координат точек поверхности
![]() .
Здесь следует отметить, что поток тепла
.
Здесь следует отметить, что поток тепла
![]() и конвективная потеря тепла
и конвективная потеря тепла
![]() не имеют места на одном и том же участке поверхности границы. Это
означает, что если существуют потери тепла за счет конвекции, то
существует отвод или приток тепла за счет теплового потока и обратно.
не имеют места на одном и том же участке поверхности границы. Это
означает, что если существуют потери тепла за счет конвекции, то
существует отвод или приток тепла за счет теплового потока и обратно.
Таким образом, уравнение (16) с приведенными граничными условиями (17) и (18) имеет единственное решение. Это решение и есть закон распределения температур в теле. Но в вариационном исчислении устанавливается, что решение подобного рода задач сводится отысканию минимума функционала [3, с. 65]:
Уравнение (16) и граничные условия (17)…(19) могут быть применены к одномерным задачам после простого вычеркивания членов, связанных с ненужными координатами. Тогда уравнение для одномерной задачи записывается в виде
с соответствующими граничными условиями
Если конвективный теплообмен отсутствует и поток тепла равен нулю, то
уравнения (23)…(24) сводятся к соотношению
![]() ,
которое выражает условие существования теплоизолированной границы.
Здесь n - внешняя нормаль.
,
которое выражает условие существования теплоизолированной границы.
Здесь n - внешняя нормаль.
В вариационном исчислении также устанавливается, что для минимизации функционала
необходимо, чтобы удовлетворялось дифференциальное
уравнение (21) и граничные условия (22)…(24). Поэтому любое
поле распределения температуры, при котором функционал (25),
становится минимальным, также удовлетворяет дифференциальным
уравнениям и, таким образом является решением поставленной задачи.
Пользуясь этим утверждением, рассмотрим стержень ограниченной длины
![]() ,
постоянный по длине площади поперечного сечения
,
постоянный по длине площади поперечного сечения
![]() .
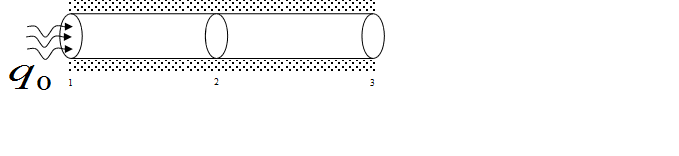
Части ее боковой поверхности теплоизолированы. На площадь поперечного
сечения левого конца подведен тепловой поток
.
Части ее боковой поверхности теплоизолированы. На площадь поперечного
сечения левого конца подведен тепловой поток
![]() ,
через площадь поперечного сечения правого конца стержня происходит
теплообмен с окружающей эту площадь средой. При этом коэффициент
теплообмена
,
через площадь поперечного сечения правого конца стержня происходит
теплообмен с окружающей эту площадь средой. При этом коэффициент
теплообмена
![]() ,
температура этой окружающей среды
,
температура этой окружающей среды
![]() .
На части площади замкнутой боковой поверхности стержня
.
На части площади замкнутой боковой поверхности стержня
![]() подведены тепловые потоки, с соответствующими интенсивностями
подведены тепловые потоки, с соответствующими интенсивностями
![]() .
Через части площади боковой поверхности стержня
.
Через части площади боковой поверхности стержня
![]() происходит теплообмен с окружающими их средами. При этом значения
соответствующий коэффициентов теплообмена примем
происходит теплообмен с окружающими их средами. При этом значения
соответствующий коэффициентов теплообмена примем
![]() .
Температуры сред, окружающих эти замкнутые поверхности обозначим
.
Температуры сред, окружающих эти замкнутые поверхности обозначим
![]() (рис. 2). Другие части боковой поверхности стержня теплоизолированы.
(рис. 2). Другие части боковой поверхности стержня теплоизолированы.
Рис. 2. Расчетная схема частично теплоизолированного стержня
Коэффициент теплового расширения и теплопроводности
материала стержня обозначим соответственно через
![]() и
и
![]() ,
модуль упругости материала через
,
модуль упругости материала через
![]() .
Единицы измерения
.
Единицы измерения
![]() ,
,
![]() и
и
![]() соответственно
будут
соответственно
будут
![]() ,
,
![]() и
и
![]() .
Предположим, что подведенные на части боковой поверхности
.
Предположим, что подведенные на части боковой поверхности![]()
![]() ,
тепловые потоки с интенсивностями
,
тепловые потоки с интенсивностями
![]() являются заданными функциями координат х. Сначала рассмотрим
первый участок стержня. Боковая поверхность этого участка
теплоизолирована. Длина участка равна
являются заданными функциями координат х. Сначала рассмотрим
первый участок стержня. Боковая поверхность этого участка
теплоизолирована. Длина участка равна
![]() .
На площадь левого конца этого участка подведен тепловой поток
интенсивности
.
На площадь левого конца этого участка подведен тепловой поток
интенсивности
![]() .
Этот участок делим на
.
Этот участок делим на
![]() равные элементы. Длина каждого элемента будет равна
равные элементы. Длина каждого элемента будет равна
![]() .
Каждый элемент рассмотрим как квадратичный конечный элемент с тремя
узлами. Тогда в этом участке стержня число узлов конечных элементов
будет равно
.
Каждый элемент рассмотрим как квадратичный конечный элемент с тремя
узлами. Тогда в этом участке стержня число узлов конечных элементов
будет равно
![]() .
Здесь рассмотрим первый элемент. В этом элементе имеется три узла с
номерами 1,2,3 (рис. 3).
.
Здесь рассмотрим первый элемент. В этом элементе имеется три узла с
номерами 1,2,3 (рис. 3).
При этом на площадь поперечного сечения, которое соответствует
первому узлу, подведен тепловой поток с интенсивностью
![]() .
Поэтому для первого конечного элемента выражения функционала, которое
характеризует полную тепловую энергию, имеет следующий вид
.
Поэтому для первого конечного элемента выражения функционала, которое
характеризует полную тепловую энергию, имеет следующий вид
здесь
![]() – объем первого квадратичного конечного элемента;
– объем первого квадратичного конечного элемента;
![]() -
площадь поперечного сечения соответствующий первому узлу
-
площадь поперечного сечения соответствующий первому узлу
![]() -го
элемента. Так как боковая поверхность рассматриваемого участка
теплоизолирована, то для всех остальных
-го
элемента. Так как боковая поверхность рассматриваемого участка
теплоизолирована, то для всех остальных
![]() -ых
элементов выражения соответствующих функционалов имеют следующий вид
-ых
элементов выражения соответствующих функционалов имеют следующий вид
Рис. 3. Первый квадратичный конечный элемент с тремя узлами
Далее рассмотрим следующий ограниченный участок
![]() стержня. Длина этого участка
стержня. Длина этого участка
![]() .
На боковую поверхность этого участка подведен тепловой поток
интенсивностью
.
На боковую поверхность этого участка подведен тепловой поток
интенсивностью
![]() ,
который зависит от координат. Этот участок делим на равные
,
который зависит от координат. Этот участок делим на равные
![]() элементов. Длина каждого элемента
элементов. Длина каждого элемента
![]() для этих элементов выражение функционала, которое характеризует
полную тепловую энергию, будет следующим
для этих элементов выражение функционала, которое характеризует
полную тепловую энергию, будет следующим
где
![]() – объем элементов;
– объем элементов;
![]() -
площадь боковой поверхности элементов.
-
площадь боковой поверхности элементов.
Далее так как боковые поверхности участков
![]() ;
;
![]() ;
;
![]() ;
стержня теплоизолированы, то каждые из участков делим на равные
;
стержня теплоизолированы, то каждые из участков делим на равные
![]() элементы. Тогда для этих элементов выражения функционалов, которые
характеризуют полную тепловую энергию, будет аналогичны (27). Так как
на боковую поверхность участка стержня
элементы. Тогда для этих элементов выражения функционалов, которые
характеризуют полную тепловую энергию, будет аналогичны (27). Так как
на боковую поверхность участка стержня
![]() подведен тепловой поток с интенсивностью
подведен тепловой поток с интенсивностью
![]() ,
то для элементов участка выражение функционала температурной энергии
выглядит следующим образом
,
то для элементов участка выражение функционала температурной энергии
выглядит следующим образом
где
![]() – число конечных элементов в этом участке стержня.
– число конечных элементов в этом участке стержня.
На участках
![]() и
и
![]() по боковым поверхностям происходит теплообмен с окружающими их
средами. При этом соответствующие коэффициенты теплообмена и
температуры окружающих сред обозначены через
по боковым поверхностям происходит теплообмен с окружающими их
средами. При этом соответствующие коэффициенты теплообмена и
температуры окружающих сред обозначены через
![]() и
и
![]() .
Для элементов этого участка выражение функционалов температурных
энергий будут следующими
.
Для элементов этого участка выражение функционалов температурных
энергий будут следующими
где
![]() и
и
![]() – число элементов на двух участках соответственно.
– число элементов на двух участках соответственно.
Теперь рассмотрим последний участок стержня
![]() .
Боковая поверхность этого участка теплоизолирована. Разделим участок
на равные
.
Боковая поверхность этого участка теплоизолирована. Разделим участок
на равные
![]() элементов. Тогда число узлов на этом участке будет
элементов. Тогда число узлов на этом участке будет
![]() .
Длина каждого элемента будет равна
.
Длина каждого элемента будет равна
![]() .
Для первых
.
Для первых
![]() элементов выражения функционалов найденных температурных энергий
будут как (27). Потому что боковые поверхности этих элементов
теплоизолированы. Но здесь
элементов выражения функционалов найденных температурных энергий
будут как (27). Потому что боковые поверхности этих элементов
теплоизолированы. Но здесь
![]() .
Для последнего
.
Для последнего
![]() -го
элемента этого участка, при написании выражения аналогичного
функционала, должно быть учтено, что через площадь поперечного
сечения правого конца этого элемента происходит теплообмен с
окружающей средой. Здесь коэффициент теплообмена
-го
элемента этого участка, при написании выражения аналогичного
функционала, должно быть учтено, что через площадь поперечного
сечения правого конца этого элемента происходит теплообмен с
окружающей средой. Здесь коэффициент теплообмена
![]() ,
а температура окружающей среды
,
а температура окружающей среды
![]() .
Тогда для последнего
.
Тогда для последнего
![]() -го
элемента стержня выражение аналогичного функционала будет иметь
следующий вид
-го
элемента стержня выражение аналогичного функционала будет иметь
следующий вид
Теперь, составляя сумму выражений функционала температурной энергии по всем элементам по длине стержня, находим выражение соответствующего функционала для рассматриваемого стержня в целом
где индекс чкэ – общее число конечных элементов в рассматриваемом стержне.
Минимизируя последний суммарный функционал по узловым значениям температур получим для их определения следующую систему линейных алгебраических уравнений получим
Таким образом, решением полученную систему известным методом Гаусса, можно определить численные значения температур в узлах конечных элементов, и далее, пользуясь соотношением (9) вычислить значение температуры в любой точке в соответствующих элементах стержня.
Выводы
Исследованием основных соотношений квадратичного конечного элемента с тремя узлами, выявлением свойств построенных функций формы и их градиентов на основе энергетического принципа и квадратичного конечного элемента построены математическая модель и соответствующий алгоритм, описывающие силовые динамические процессы стержня с учетом заданных тепловых потоков, теплообменов и теплоизоляции. Построены разрешающие системы линейных алгебраических уравнений. Предложенную методику можно применить при проектировании машин, где рабочие органы, помимо механических нагрузок испытывают также и температурные напряжения, предусмотренные при их созданий и (или) в процессе эксплуатации.
- Литература:
Тулеуова Р.О., Макатова В.Е. Задачи теплопроводности в упруго-деформированных элементах // Вестник КазНУ им. Аль-Фараби. Алматы, 2001. – 185 с.
Ахметов С.М., Махатова В.Е., Тулеуова Р.О., Боздаков А. Математическая модель и вычислительный алгоритм расчета термонапряженно-деформированного состояния стержня ограниченной длины при наличии теплового потока, теплообмена и осевой растягивающей силы / Сб. докл. межд. научно-практ. конференции «Атырауский государственный университет им. Х.Досмухамедова – служение образованию и науке региона больше полувека». В трех томах. Атырау, 2010. Том II. – 214 с.
Петров А.В. Задачи термодинамики в приложении техники: М.: Наука, 1985. – 286 с.
Похожие статьи
Треугольный конечный элемент с узловыми неизвестными в виде...
Приводятся расчет объемного конечного элемента треугольной формы поперечного сечения при различных вариантах аппроксимации перемещений. Ключевые слова: оболочка, объемный треугольный конечный элемент, несжимаемый материал, напряжения, деформации...
Четырехугольный конечный элемент с узловыми неизвестными...
Приведен расчет объемного конечного элемента четырехугольной формы поперечного сечения при различных вариантах аппроксимации перемещений. Ключевые слова: Четырехугольный конечный элемент, полином, матрица-строка...
Алгоритм расчет теплообменного аппарата | Статья в журнале...
Тепловой поток, воспринимаемый паровой средой: Отсюда: − расход воды на УПГ.
Коэффициент утилизации теплоты: . Расчет геометрических характеристик поверхностей нагрева.
Поверхность нагрева элементов УПГ
Сопряжённый теплообмен при движении вязкой несжимаемой...
Условия неразрывности тепловых потоков и непротекания заданы на линии симметрии ( ).
На возвратном участке движения поперечная составляющая скорости начинает расти.
С уменьшением длины входного участка максимальное значение функции U(X) по сечениям...
Экспериментальное исследование теплообмена при струйном...
Благодаря отсутствию необогреваемого участка в начале струи, динамический и тепловой пограничные
Рис. 4. Местный коэффициент теплообмена раходящейся струи при различных SR. Как видно, благодаря влиянию поперечной кривизны обтекаемой поверхности...
Интенсификация теплообмена в каналах | Статья в журнале...
Во всех нижеприведенных зависимостях при вычислении коэффициентов теплоотдачи в трубах с кольцевыми турбулизаторами и в пучках труб увеличение поверхности теплообмена не учитывалось, т. е. плотность теплового потока определялась по поверхности гладкой...
Метод определения площади дефектных участков поверхности...
Ключевые слова: определения площади дефектных участков, коэффициент излучения материала, погрешность тепловизионного контроля
Основные термины (генерируются автоматически): RGB, рассматриваемая поверхность, тепловой поток, участок, температура...
Исследование температурных полей в методе неразрушающего...
1. Не соблюдается условие соответствия тепловой системы одной из классических моделей теплопереноса, например, модели полупространства.
Принимаем, что все элементы схемы находятся в идеальном тепловом контакте друг с другом. Боковые поверхности тел имеют...
Коэффициент формы как геометрическая характеристика
Коэффициент формы плоской области является количественной характеристикой формы области и выражается через контурный интеграл.
Требуется найти выпуклую фигуру вращения максимальной площади поверхности: (4). опорная функция , которой удовлетворяет условиям.
Похожие статьи
Треугольный конечный элемент с узловыми неизвестными в виде...
Приводятся расчет объемного конечного элемента треугольной формы поперечного сечения при различных вариантах аппроксимации перемещений. Ключевые слова: оболочка, объемный треугольный конечный элемент, несжимаемый материал, напряжения, деформации...
Четырехугольный конечный элемент с узловыми неизвестными...
Приведен расчет объемного конечного элемента четырехугольной формы поперечного сечения при различных вариантах аппроксимации перемещений. Ключевые слова: Четырехугольный конечный элемент, полином, матрица-строка...
Алгоритм расчет теплообменного аппарата | Статья в журнале...
Тепловой поток, воспринимаемый паровой средой: Отсюда: − расход воды на УПГ.
Коэффициент утилизации теплоты: . Расчет геометрических характеристик поверхностей нагрева.
Поверхность нагрева элементов УПГ
Сопряжённый теплообмен при движении вязкой несжимаемой...
Условия неразрывности тепловых потоков и непротекания заданы на линии симметрии ( ).
На возвратном участке движения поперечная составляющая скорости начинает расти.
С уменьшением длины входного участка максимальное значение функции U(X) по сечениям...
Экспериментальное исследование теплообмена при струйном...
Благодаря отсутствию необогреваемого участка в начале струи, динамический и тепловой пограничные
Рис. 4. Местный коэффициент теплообмена раходящейся струи при различных SR. Как видно, благодаря влиянию поперечной кривизны обтекаемой поверхности...
Интенсификация теплообмена в каналах | Статья в журнале...
Во всех нижеприведенных зависимостях при вычислении коэффициентов теплоотдачи в трубах с кольцевыми турбулизаторами и в пучках труб увеличение поверхности теплообмена не учитывалось, т. е. плотность теплового потока определялась по поверхности гладкой...
Метод определения площади дефектных участков поверхности...
Ключевые слова: определения площади дефектных участков, коэффициент излучения материала, погрешность тепловизионного контроля
Основные термины (генерируются автоматически): RGB, рассматриваемая поверхность, тепловой поток, участок, температура...
Исследование температурных полей в методе неразрушающего...
1. Не соблюдается условие соответствия тепловой системы одной из классических моделей теплопереноса, например, модели полупространства.
Принимаем, что все элементы схемы находятся в идеальном тепловом контакте друг с другом. Боковые поверхности тел имеют...
Коэффициент формы как геометрическая характеристика
Коэффициент формы плоской области является количественной характеристикой формы области и выражается через контурный интеграл.
Требуется найти выпуклую фигуру вращения максимальной площади поверхности: (4). опорная функция , которой удовлетворяет условиям.