Прогнозирование частоты вызовов скорой помощи на основе интеллектуального анализа данных

В работе предлагается использование классификационных моделей для прогнозирования количества вызовов скорой помощи в зависимости от климатических условий, состояния магнитосферы и степени загрязненности воздуха. Вывод моделей сделан с помощью софтуерного пакета WEKA на обучающем множестве из 366 записей, соответствующих вызовам станции скорой помощи в Санкт-Петербурге в течение года. Точность прогнозирования с помощью полученных моделей — в диапазоне 67,53 %-76.64 %. Сравнительно невысокая точность прогноза на данном этапе может быть повышена за счет увеличения обучающей выборки и оптимизации данных для классификации.

Ключевые слова: классификация, алгоритмы классификации, количество вызовов скорой помощи, климатические условия, прогнозирование.

I. Введение

Прогнозирование числа вызовов скорой медицинской помощи и обеспечение необходимого для нормального их обслуживания количества бригад является важным фактором качественного оказания медицинской помощи. В некоторых случаях задержка в обслуживании является критической в деле спасения человеческой жизни. Поэтому изучению факторов, которые влияют на здоровье и самочувствие человека и, соответственно, на частоту вызовов скорой помощи, посвящено огромное количество исследований.

В работе [1] исследуется отрицательное влияние жаркой погоды на здоровье человека в городских сообществах. В целях предсказания вредных метеорологических условий и готовности к ним во многих городах Канады были разработаны и реализованы системы медицинских предупреждений о наступлении жары (HHWS). Авторы установили, что в целом временная структура звонков 911(аналогично 03 в России) соответствует временной структуре оповещения о наступлении высоких температур через систему HHWS и структуре выездов бригад по вызовам в отделениях неотложной помощи по поводу болезней и состояний, связанных с жаркой погодой.

Авторы [2] используют oбобщенные aддитивные модели [3] для установления связи между биометеорологическими условиями и частотой вызовов скорой помощи. Они установили, что в диапазоне температур между 25 и 30 °C процентное изменение числа вызовов, связанное с повышением температуры воздуха на каждый 1°C составляет 1,45 % для заболеваний терапевтического профиля и 2.74 % для заболеваний дыхательных путей в частности. Эта закономерность наблюдается только для температур выше 25°C Влияние температуры на частоту вызовов исследовалось и в работе [4]. Авторы установили, что заболеваемость увеличилась экспоненциально с температурой выше 15,6 °C. Коэффициент увеличения количества вызовов на каждый 1 градус повышения среднедневной температуры по сравнению с 15,6°C составляет 1.43. Температурные воздействия влияли максимально на 45–64-летних пациентов, больше на мужчин, чем на женщин, и больше на жителей сельских округов, чем на городских жителей.

Исследователи [5] использовали однофакторный дисперсионный анализ и множественную линейную регрессию для установления корреляции между суточным числом пациентов различного уровня неотложности и различными заболеваниями со среднесуточной температурой (Т) и изменением температуры (dt) по сравнению с предыдущим днем. Исследования показали, что температура окружающей среды имеет дифференцированное воздействие на пациентов скорой помощи с различными заболеваниями и различной степенью тяжести заболевания. Авторы [6] анализируют влияние погодных эффектов и возрастно-половой структуры населения на количество вызовов с целью обеспечения лучшего планирования ресурсов в будущем. Они использовали информацию о более чем 2-х миллионах случаев вызовов неотложной помощи в Гонконге в 2008 году для прогнозирования спроса услуг скорой помощи в 2036. Прогноз сделан с учетом прогнозируемых изменений в возрастно-половой структурe между 2008 и 2036.

В работе [7] сообщается, что повышенные концентрации грубодисперсных твердых частиц в воздухе ведет к увеличению количества вызовов скорой помощи по поводу респираторных заболеваний у взрослого населения (в возрасте 65 лет и старше). В [8] исследуется влияние фазы полной и новой луны на изменение частоты проведения сердечно-легочных реанимаций. За время 4018-дневного периода исследования были сделаны 2 370 233 посещения пациентов бригадами отделений неотложной помощи, из них 6827 требующие сердечно-легочной реанимации. Авторы не обнаружили значимых различий по частоте проведения сердечно-легочной реанимации во время полнолуния. В то же время в дни новолуния потребовалось проведение сердечно-легочной реанимации в среднем на 6.5 % меньше, чем в другие дни.

Авторы [9] отмечают, что прогнозирование количества вызовов скорой помощи на основе официального прогноза погоды осуществимо. Они разработали модель линейной множественной регрессии, описывающую связь между количеством звонков, связанных с медицинскими проблемами, и метеорологическими временными сериями данных. Метеорологические переменные, рассмотренные в данном исследовании, включали в себя среднюю температуру (Т), разницу средних температур на протяжении двух дней подряд, среднюю относительную влажность (RH), среднee атмосферное давление и взаимодействие между T и RH. Для учета времени запаздывания погодных эффектов использовались данные с отставанием на 4 дня [10].

В работе [11] дается обзор ключевых методов моделирования, использованных для анализа и прогнозирования нагрузки отделений неотложной помощи: методы, основанные на формулах [11–15]; регрессионное моделирование [14, 16–18]; aнализ временных рядов [16, 19–22], модели на основе теории массового обслуживания [23–26], дискретно-событийное моделирование (discrete-event simulation, DES) [27–30]. Aвторы [11] обобщают, что из-за специфики операций, выполняемых в отделениях неотложной помощи, их точное моделирование является сложной задачей. Каждый из применяемых подходов имеет свои преимущества, но и существенные ограничения, которые не позволяют полностью охватить всю сложность системы работы неотложной помощи.

В настоящей работе использутся инструмент классификации интеллектуального анализа данных (data mining) для определения „класса” нагрузки станции скорой помощи на базе атрибутов, формированных на основе статистических данных о погоде, магнитных бурях и загрязненности атмосферы.

II.     Использованная методика

В машинном обучении [31,32] классификация относится к стратегиям обучения с учителем (supervised learning) или управляемого обучения. Под классификацией понимают задачу определения категории, к которой принадлежит ранее не встречавшийся объект, на основании обучающего множества, для элементов которого эти категории известны. Цель процесса классификации — построение модели, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута (класса). Обучающее множество (training set) содержит входные и выходные данные, используемые для конструирования модели. Тестовое множество (test set) содержит аналогичный набор данных для проверки работоспособности модели.

II.1. Множествa данных

На данном этапе располагаемая нами база данных включает значения количеств вызовов скорой помощи на двух расположенных по соседству станциях Санкт-Петербурга в 2012 году. Среднее количество вызовов на двух станциях имеет аналогичный ход в течение года — с минимумом в летние месяцы (рис. 1).

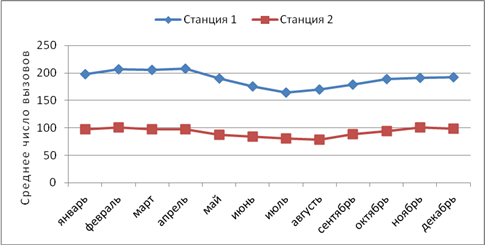
Рис. 1. Среднемесячное число вызовов на двух станциях скорой помощи

В течение каждого месяца количество вызовов колеблется в довольно широких границах (рис.2, табл. 1). В данном исследовании в качестве обучающего множества для модели классификации используются данные по первой станции, а в качестве тестового множества — данные по второй станции. Для сопоставимости двух множеств классификация ведется по относительному изменению количества вызовов (табл. 1).

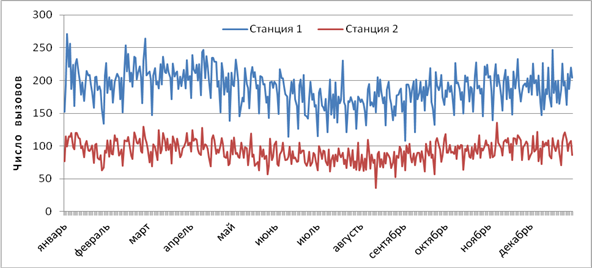
Рис. 2. Число вызовов на двух станциях скорой помощи по дням 2012 года

Таблица 1

Статистика количества вызовов

В рассматриваемой задаче количество вызовов является выходным значением классификации или зависимым атрибутом (классом).

II.2. Атрибуты

Классификация осуществлялaсь на основе климатических данных [33], состояния магнитосферы [34] и показателей загрязненности воздуха [35].

Таблица 2

Использованные атрибуты

Таблица 3

Дискретизация непрерывных данных

Анализ входных атрибутов (признаков, показателей) классификации средствами WEKA показал, что абсолютное значение температуры не имеет значимого прогностического значения. Влияние на количество вызовов оказывает степень соответствия температуры сезону, задаваемая атрибутом Tlevel. Числовое значение Tlevel определяется как разница дневной температуры и среднестатистической температуры для данного месяца по данным [36]. Также при предварительной обработке отстранены данныe для воскресных дней — в данной выборке им соответствовало малое число вызовов независимо от показателей классификации. Поэтому день недели не включен в список атрибутов. В связи с малым объемом располагаемой базы данных в классификации используются номинальные атрибуты, т. е. атрибуты, принимающие перечисленное множество значений (табл. 2, 3).

II.3. Классификация

Существует множество подходов к классификации: вероятностные методы, деревья принятия решений, нейронные сети и многие другие [31, 32]. В работе использованы три метода классификации, дающие удовлетворительные результаты для рассматриваемой задачи: HNB, RandomForest и MultilayerPerceptron.

Алгоритм HNB (Hidden Naïve Bayes) [38,39] oтносится к вероятностным моделям классификации. Наиболее известный и широко применяемый классификатор этого класса моделей — наивный байесовский классификатор (NB). Несмотря на свою простоту, в ряде случаев он дает результаты классификации лучше, чем более усовершенствованные модели. NB классификатор является простейшей формой байесовской сети. В ней каждый узел атрибута имеет узел класса в качестве родителя, причем предполагается условная независимость атрибутов классификации. Существует ряд модификаций NB классификатора, которые различными способами снимают ограничение независимости. В модели NHB создается скрытый родитель для каждого атрибута, который учитывает влияния всех других атрибутов. HNB наследует структурную простоту наивного байесовского классификатора. В то же время, с точки зрения точности классификации, он превосходит NB и ряд других алгоритмов классификации [38].

Алгоритм классификации Random Forest („случайный лес”) [31, 32, 40] относится к методам, основанным на деревьях решений. Дерево принятия решений — способ представления правил в иерархической структуре. Оно состоит из узлов и листьев, соответствующих значениям класса. Для классификации объекта, не вошедшего в обучающее множество, осуществляется поиск, начиная с корня, до обнаружения класса, соответствующего объекту. Одиночное дерево решений представляет собой слабый классификатор — оно дает высокую дисперсию и высокую систематическую ошибку. Случайный лес объединяет несколько деревьев решений для принятия решения классификации. Путем усреднения по всему ансамблю деревьев уменьшается дисперсия окончательной оценки. Случайные леса обеспечивает хорошую точность и работают эффективно на больших наборах данных. Кроме того, с их помощью можно оценить относительную важность признаков для классификации.

Multilayer Perceptrons (MLPs) [31, 32, 41] — многослойныe персептроны являются нейросетевые модели, с помощью которых можно аппроксимировать любую непрерывную функцию. MLPs состоят из нейронов, называемых персептронами. Персептрон получает в качестве входных данных характеристики (x₁, х₂, …, х_n), каждая из которых имеет определенный вес w_i. Входные характеристики передаются входной функции U, котороя вычисляет их взвешенную сумму 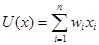. Результат этого вычисления передается функции активации F, которая определяет выход персептрона F(U(x)). Универсальные аппроксимационные возможности MLPs достигаются путем объединения нескольких нейронов, организованных по крайней мере в трех слоях (один входной слой; один или более скрытые слои; один выходной), а также за счет использования различных функций активации. Для скрытых слоев нейронов часто используется сигмовидная активационная функция. Как правило, для задач классификации функция активации выходного слоя нейронов также сигмовидная. Обучение в MLPs также состоит в корректировке весов персептронов так, чтобы обеспечить минимум ошибки на обучающих данных. Традиционно для этой цели используется алгоритм обратного распространения [41], но могут быть использованы и другие алгоритмы. Существуют стратегии для избежания переобучения сети, т. е. для избежания создания моделей, которые имеют плохое прогностическое моделирование из-за случайной ошибки или шума в обучающих данных..

Таблица 4

Результаты классификации

Классификация по описанным методам выполнeна с помощью библиотеки алгоритмов машинного обучения WEKA [42]. Полученные результаты приведены в таблице 4. Большое уменьшение точности классификации тестового множества по сравнению с обучающим свидетельствует о невысокой надежности моделей классификации, что можно объяснить небольшим объемом обучающего множества и соответственно грубой дискретизацией целевого атрибута (класса).

Несмотря на сравнительно невысокую точность полученных классификационных моделей, они могут быть полезны при планировании количества медицинского персонала, необходимого для качественного обслуживания населения. На рис.3 показана матрица ошибок (confusion matrix) при классификации по алгоритму Random Forest. В 68 из 90-ти случаев модель правильно прогнозирует увеличенное число вызовов, что дает возможность руководству станции предусмотреть большее число бригад в эти дни.

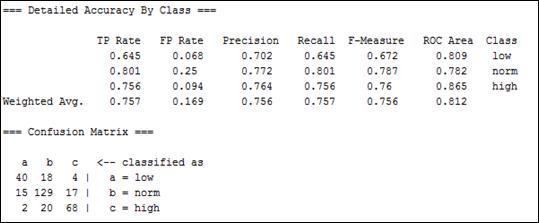
Рис. 3. Результаты классификации тестового множества по методу RandomForest

На рис.4 показаны результаты выбора значимых входных атрибутов, выполненного инструментом Select аttributes с настройками по умолчанию в WEKA. Из 13-ти входных атрибутов в первоначальной базе данных (табл.2) выбраны 7: уровни температуры, давления и влажности, загрязнение воздуха, магнитные бури и изменение температуры воздуха на протяжении двух дней подряд с опозданием на 4 и 5 дней. Таким образом, модель классификации подтверждает цитированное многими исследователями (например, [10]) воздействие температурных изменений на здоровье с опозданием (lag) в несколько дней.

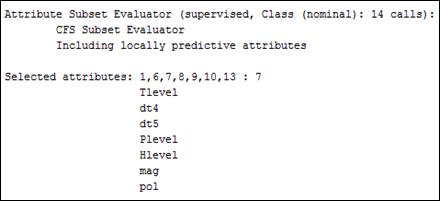
Рис. 4. Результаты выбора наиболее значимых атрибутов классификации

III.  Выводы

Получены модели классификации, с помощью которых можно прогнозировать ожидаемое количество вызовов на станциях скорой помощи на базе метеорологических данных, данных о загрязненности воздуха и магнитных бурях. Наилучшую точность классификации — около 76 %, дают реализованные в библиотеке алгоритмов машинного обучения WEKA 3.6.10 методы RandomForest и MultilayerPercepron. Метод HNV дает точность классификации около 67 %, но характеризуется наибольшим быстродействием. В будущих исследованиях авторы ожидают улучшение точности моделей за счет увеличения размера обучающего множества

Литература:

1.         Bassil KL, Cole DC, Moineddin R, Craig AM, Lou WY, Schwartz B, Rea E. Temporal and spatial variation of heat-related illness using 911 medical dispatch data. Environ Res. 2009, 109:600–606

2.         Alessandrini E, Zauli Sajani S, Scotto F, Miglio R, Marchesi S, Lauriola P. Emergency ambulance dispatches and apparent temperature: a time series analysis in Emilia-Romagna, Italy. Environ Res. 2011, 111(8):1192–1200

3.         Hastie T, Tibshirani P. Generalized Additive Models http://web.stanford.edu/~hastie/Papers/gam.pdf

4.         Lippmann SJ, Fuhrmann CM, Waller AE, Richardson DB. Ambient temperature and emergency department visits for heat-related illness in North Carolina, 2007–2008. Environ Res. 2013,124:35–42

5.         Tai CC,  Lee CC, Shih CL, Chen SC. Effects of ambient temperature on volume, specialty composition and triage levels of emergency department visits. Emerg Med J. 2007, 24(9): 641–644

6.         Lai PC, Wong HT. Weather and age-gender effects on the projection of future emergency ambulance demand in Hong Kong. Asia Pac J Public Health. 2015, 27(2): NP2542–NP2554

7.         Michikawa T, Ueda K, Takeuchi A, Tamura K, Kinoshita M, Ichinose T, Nitta H. Coarse particulate matter and emergency ambulance dispatches in Fukuoka, Japan: a time-stratified case-crossover study. Environ Health Prev Med. 2015;20(2):130–136

8.         Alves DW, Allegra JR, Cochrane DG, Cable G. Effect of lunar cycle on temporal variation in cardiopulmonary arrest in seven emergency departments during 11 years. Eur J Emerg Med. 2003, 10(3):225–228

9.         Wong HT, Chiu MY, Wu CS, Lee TC. The influence of weather on health-related help-seeking behavior of senior citizens in Hong Kong. Int J Biometeorol. 2015, 59(3):373–376

10.     Wong HT, Lai PC. Weather inference and daily demand for emergency ambulance services in Hong Kong. Emerg Med J 2012, 29: 60–64

11.     Wiler JL1, Griffey RT, Olsen T. Review of modeling approaches for emergency department patient flow and crowding research. Acad Emerg Med. 2011, 18(12):1371–1379

12.     12 Bernstein SL, Verghese V, Leung W, Lunney AT, Perez I. Development and validation of a new index to measure emergency department crowding. Acad Emerg Med. 2003, 10:938–942.

13.     Epstein SK, Tian L. Development of an emergency department work score to predict ambulance diversion. Acad Emerg Med. 2006, 13:421–426.

14.     Hoot N, Aronsky D. An early warning system for overcrowding in the emergency department. AMIA Annu Symp Proc. 2006:339–43.

15.     Reeder TJ, Garrison HG. When the safety net is unsafe: real-time assessment of the overcrowded emergency department. Acad Emerg Med. 2001, 8:1070–10744

16.     Jones SS, Thomas A, Evans RS, Welch SJ, Haug PJ Snow GL. Forecasting daily patient volumes in the emergency department. Acad Emerg Med. 2008; 15:159–167

17.     Weiss SJ, Derlet R, Arndahl J, et al. Estimating the degree of emergency department overcrowding in academic medical centers: results of the national ED overcrowding study (NEDOCS). Acad Emerg Med. 2004, 11:38–50.

18.     Batal H, Tench J, McMillian S, Adams J, Mehler PS. Predicting patient visits to an urgent care clinic using calendar variables. Acad Emerg Med. 2001, 8:48–53

19.     Milner PC. Ten-year follow-up of ARIMA forecasts of attendances at accident and emergency departments in the Trent region. Stat Med. 1997, 16:2117–25.

20.     Champion R, Kinsman LD, Lee GA, et al. Forecasting emergency department presentations. Aust Health Rev. 2007, 31:83–90.

21.     Tanberg D, Qualls C. Time series forecasts of emergency department patient volume, length of stay, and acuity. Ann Emerg Med. 1994, 23:299– 306.

22.     Schweigler LM, Desmond JS, McCarthy ML, Bukowski KJ, Ionides EL, Younger JG. Forecasting models of emergency department crowding. Acad Emerg Med. 2009, 16:301–308.

23.     Au L. Predicting overflow in an emergency department. IMA J Manag Math. 2009, 20:39–49.

24.     Cochran JK, Roche KT. A multi-class queueing network analysis methodology for improving hospital emergency department performance. Computers Operations Res. 2009, 36:1497–1512.

25.     Siddharthan K, Jones WJ, Johnson JA. A priority queueing model to reduce waiting times in emergency care. Int J Health Care Qual Assur. 1996, 9: 10–16.

26.     Green LV, Soares J, Giglio JF, Green RA. Using queueing theory to increase the effectiveness of emergency department provider staffing. Acad Emerg Med. 2006, 13:61–68

27.     Hoot NR, LeBlanc LJ, Jones I, et al. Forecasting emergency department crowding: a discrete event simulation. Ann Emerg Med. 2008, 52:116–125.

28.     Connelly LG, Bair AE. Discrete event simulation of emergency department activity: a platform for system- level operations research. Acad Emerg Med. 2004, 11:1177–1185

29.     Coats TJ, Michalis S. Mathematical modeling of patient flow through an accident and emergency department. Emerg Med J. 200, 18:190–192.

30.     Hung GR, Whitehouse SR, O’Neill C, Gray AP, Kissoon N. Computer modeling of patient flow in a pediatric emergency department using discrete event simulation. Pediatr Emerg Care. 2007, 23:5–10.

31.     Theodoridis, S. Machine Learning, Academic Press, 2015

32.     Larose CD, Larose DT. Data Mining and Predictive Analytics, 2nd Edition John Wiley & Sons, 2015

33.     Архив погоды в Санкт-Петербурге с 1999 года http://pitermeteo.ru/archive.php

34.     Maгнитние буди онлайн http://www.tesis.lebedev.ru/magnetic_storms.html?m=1&d=16&y=2012

35.     Качество атмосферного воздуха по данным Автоматической системы мониторинга атмосферного воздуха http://www.infoeco.ru/index.php?id=53

36.     Климат Санкт-Петербурга http://www.pogodaiklimat.ru/climate/26063.htm

37.     Нормы влажности http://tatjanacit.narod.ru/p5aa1.html

38.     Zhang H, Jiang L, Su J. Hidden Naive Bayes, 2005. http://www.csie.ntu.edu.tw/~r95038/Try/paper/Hidden %20Naive %20Bayes.pdf

39.     Jiang L; Zhang H,  Cai Z. A Novel Bayes Model: Hidden Naive Bayes. Knowledge and Data Engineering, IEEE Transactions on  2009, 21 (10): 1361–1371

40.     Liaw A, Wiener M. Classification and Regression by randomForest. 2002, http://www.bios.unc.edu/~dzeng/BIOS740/randomforest.pdf

41.     Gurney K. Introduction to neural networks. United Kingdom: Taylor and Francis; 2005.

42.     Hall,M., E.Frank, G. Holmes, B.Pfahringer, P.Reutemann, I. H. Witten, 2009. The WEKA Data Mining Software: An Update; SIGKDD Explorations, 11(1) http://www.cs.waikato.ac.nz/ml/weka/