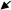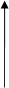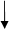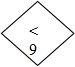Игры с математическим содержанием как средства развития логических операций мышления у детей старшего дошкольного возраста

В современной педагогике дидактическая игра рассматривается, как эффективное средство развития ребёнка, развитие таких интеллектуальных психических процессов как внимание, память, мышление, воображение.

Обучение через игру – интересное и увлекательное занятие. Способствует постепенному переносу интереса и увлеченности с игровой на учебную деятельность. Игра, увлекающая детей, их не перегружает ни умственно, ни физически. Очевидно, что интерес детей к игре постепенно переходит не только в интерес к учению, но и к тому, что изучается, т.е. интерес к математике. Поддерживаемый же интерес к изучению математики с самого раннего возраста снимает многие из трудностей, возникающих на пути усвоения математических знаний. Устойчивый интерес к изучению математики должен поддерживаться различными методами на всех этапах обучения.

Математическими играми считаются игры, в которых смоделированы математические построения, отношения, закономерности. Для нахождения ответа (решения), как правило, необходим предварительный анализ условий, правил, содержание игры или задачи. По ходу решения требуется применение математических методов и умозаключений.

Разновидностью математических игр и задач являются логические игры, задачи, упражнения. Они направлены на тренировку мышления при выполнении логических операций и действий. С целью развития мышления детей используют различные виды несложных задач и упражнений. Это задачи на нахождение пропущенной фигуры, продолжение ряда фигур, на поиск чисел, недостающих в ряду фигур (нахождение закономерностей, лежащих в основе выбора этой фигуры и т. д.)

Следовательно, логико-математические игры – это игры, в которых смоделированы математические отношения, закономерности, предполагающие выполнение логических операций и действий.

В логико-математических играх и упражнениях используются специальный структурированный материал, позволяющий наглядно представить абстрактные понятия и отношения между ними.

Идеи простейшей предматематической подготовки дошкольников большое внимание уделял А. А. Столяр. Его методика введения детей в мир ло­гико-математических представлений — свойства, отношения, множества, операции над множествами, логические операции (отрицание, конъюнкция, дизъюнкция) — осуществлялась с по­мощью специальной серии обучающих игр. [1]

Обучающая функция игр порождает особенности, отличающие их от дидактических игр, используемых лишь для закрепления того, что уже усвоено с помощью других методов.

Система обучающих игр состоит из отдельных серий. Каждая серия игр предназначена для формирования определенных структур мышления или подготовки к усвоению определенного блока знаний. Внутри каждой серии игры располагаются в определенной последовательности таким образом, что задачи, решаемые в процессе игровой деятельности, постепенно усложняются.

Например, серии игр с обручами (группировка предметов по определенному признаку). Наиболее простыми являются игры с одним обручем (группировка объектов по одному признаку в одно множество), затем проводятся игры с двумя обручами (группировка в два множества) и, наконец, наиболее сложные задачи решаются шестилетними детьми в играх с тремя обручами (группировка в три множества и по нескольким признакам одновременно).[2,с. 45]

В обучающих играх есть еще одна особенность, отличающая их от традиционных дидактических игр, — большая вариативность условий, правил, задач, решаемых в процессе игровой деятельности. Благодаря этой особенности многократное повторение обучающей игры одной и той же серии включает определенные элементы новых знаний, которые приобретаются детьми. Кроме того, и это тоже немаловажно, постоянное обновление при повторении игр одной серии поддерживает интерес детей к игре,

Обучающая игра выполняет еще одну важную функцию обучения — развивающую, формируя познавательные процессы, способности ребенка.

В таких играх зарождаются и развиваются многие личностные качества: самостоятельность и коллективизм, инициативность и трудолюбие, целеустремленность и сообразительность, уверенность и любознательность. Дети начинают сознавать, что, хотя предстоит играть в уже известную игру, в ней обязательно будет что-то новое, интересное.

Наряду с обучающими играми, формирующими определенные представления, необходимо широко практиковать и такие, в которых моделируются определенные структуры мышления, т.е. игры, обучающие мыслить.

Освещая данный аспект, приведем в качестве примера такую задачу: «Сколько нужно вынуть шариков из мешочка, в котором находятся три красных и три желтых шарика, чтобы заранее можно было с уверенностью сказать, что, по крайней мере, один из вытянутых будет обязательно красным?»

Эта задача затрудняет многих дошкольников и, конечно, недоступна детям 5 – 6 лет. Однако она становится доступной им после проведения серии игр.

Серия игр «Чудо мешочек» (А.А. Столяр).

1. Первая игра. Детям показывают пустой мешочек и два шарика: красный и желтый, затем кладут шарики в мешочек. На вопрос: «Сколько шариков в мешочке?» дети отвечают: «В мешочке два шарика, один красный, другой желтый». Игра состоит в том, что дети поочередно, не глядя в мешочек, вынимают один шарик, называют его цвет и снова кладут в мешочек. Таким образом, обнаруживается, что вынутый шарик может оказаться красным или желтым и что заранее нельзя сказать, какого цвета шарик будет вынут из мешочка.

Вторая игра. В мешочек кладут два красных и два желтых шарика, повторяются опыты по вытаскиванию одного шарика. Затем переходят к выбору двух шариков. После достаточного числа повторений этих опытов обнаруживается, что если из мешочка вынимать, не глядя в него, два шарика, то они могут оказаться оба красными, или оба желтыми, или один красный и один желтый. Дети сами убеждаются в том, что других вариантов нет.

Далее проводятся опыты по выбору трех шариков. Легко обнаруживается, что в этом случае возможны лишь два варианта: либо будут вынуты два красных шарика и один желтый, либо один красный и два желтых. После этих опытов предлагается задача: «Сколько шариков надо вынуть из мешочка, чтобы хотя бы один из вынутых шариков оказался красным?»

Вначале, естественно, у детей возникают некоторые затруднения. Требуется разъяснение, что означает выражение «хотя бы один». Однако некоторые дети быстро догадываются, что надо вынуть три шарика. После того как выясняется, почему достаточно вынуть три шарика, это становится понятным многим детям, а после нескольких повторений игры все дети решают задачу.

Особое значение для формирования дисциплины ума имеют игры, в которых дети выполняют определенные действия, предписанные некоторым алгоритмом «Преобразование слов», или программой «вычислительной машины», работу которой они имитируют. [3, с. 53]

Серия игр «Вычислительные машины II».

Играют двое. Первый — ведущий. Он разъясняет усло­вие игры, определяет задания. Второй, выполняет роль вычислительной машины. Игра проводит­ся в несколько этапов.

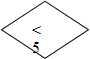
1.Ведущий подает на вход машины (желтый круг) какое-нибудь од­нозначное число, например 3; другой, выполняющий роль вычислительной машины, должен, прежде всего, проверить, выполняется ли условие «<5»: 3<5—«да». Условие выполняется, и он должен продвигаться дальше по стрелке, помеченной словом «да», т. е. к этому числу прибавить 2, а на выходе машины (красный круг) показать карточку с числом 5. Если же условие «<5» не выполняется, то машина продвигается по стрелке, по­меченной словом «нет», и вычитает 2. (рисунок 1.)

Рис. 1 Вычислительные машины ІІ

1 2 3

да нет А

=2 Б да

нет

В

2. При организации игры по рисунку А ведущий помещает на «вход» какое-либо число. Второй должен выполнить указанное действие. В дан­ном случае прибавить 3. Игру можно модифицировать, заменив задание в квадратике. Играя по рисунку Б, второй играющий должен узнать то число, ко­торое помещено на «входе». Ведущий может изменять не только число на «выходе» (в красном круге), но и задание в квадратике.

При игре по рисунку В требуется указать то действие, которое сле­дует выполнить, чтобы из числа на «входе» получилось то число, кото­рое <указано на «выходе». Ведущий может менять либо число на «входе», либо на «выходе», либо оба этих числа одновременно.

3. Ведущий подает на «вход» какое-нибудь однозначное число. Игрок,
выполняющий роль вычислительной машины, прибавляет к этому числу
двойки до тех пор, пока не получится число, не меньшее 9, т. е. большее или
равное 9. Это число и будет результатом, его игрок покажет на «выходе»
машины с помощью карточки с соответствующей цифрой.

Например, если на «вход» поступило число 3, машина прибавляет к нему число 2, затем проверяет, будет ли полученное число (5) меньше 9. Так как условие 5<9 выполняется («да»), то машина продвигается по стрелке, помеченной словом «да», и опять повторяет то, что уже выпол­нила раз, т. е. прибавляет к числу 5 число 2 и проверяет, будет ли по­лученное число 7 меньше 9. Так как ответ на вопрос, выполняется ли ус­ловие 7<9,—«да», то машина опять продвигается по стрелке, помеченной словом «да», т. е. опять повторяет уже выполненные дважды действия: прибавляет к числу 7 число 2 и проверяет условие 9<9. Так как это условие не выполняется, то машина продвигается по стрелке, помечен­ной словом «нет», в красный круг помещает карточку с числом 9 и оста­навливается. [4, с. 60]

Итак, математические игры позволяют на доступном детям математическом материале, с опорой на жизненный опыт строить правильные суждения без предварительного теоретического освоения самих законов и правил логики.

Математика может и должна играть особую роль в гуманизации образования, т.е. в его ориентации на воспитание и развитие личности. Знания нужны не ради знаний, а как важная составляющая личности, включающая умственное, нравственное, эмоциональное и физическое воспитание и развитие. Особая роль математики – в умственном воспитании, в развитии интеллекта.

Литература:

1. Формирование элементарных математических представлений у дошкольников: Учеб. пособие для студентов пед. институтов /Р.Л. Березина, З.А.Михайлова, и др.; Под ред. А.А. Столяра. – М.: Просвещение, 1988. – 303 с.

2. Давайте поиграем: Мат. Игры для детей 5-6 лет: Кн. Для воспитателей дет. сада и родителей / Н.И. Касабуцкий, Г.Н. Скобелев, А.А. Столяр, Т.М. Чеботаревская; Под ред. А.А. Столяра. – М.: Просвещение, 1991. –с. 45

3. Давайте поиграем: Мат. Игры для детей 5-6 лет: Кн. Для воспитателей дет. сада и родителей / Н.И. Касабуцкий, Г.Н. Скобелев, А.А. Столяр, Т.М. Чеботаревская; Под ред. А.А. Столяра. – М.: Просвещение, 1991. –с. 53

4. Давайте поиграем: Мат. Игры для детей 5-6 лет: Кн. Для воспитателей дет. сада и родителей / Н.И. Касабуцкий, Г.Н. Скобелев, А.А. Столяр, Т.М. Чеботаревская; Под ред. А.А. Столяра. – М.: Просвещение, 1991. –с. 60