В настоящей работе рассматривается система дифференциальных уравнений нейтрального типа с переменным отклонением аргумента вида
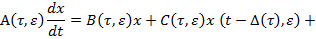
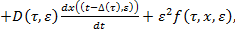 (1)
(1)
где 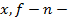 мерные векторы, из них
мерные векторы, из них  искомый,
искомый, 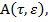
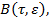
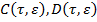 — квадратные матрицы
— квадратные матрицы 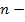 го порядка, допускающие разложения.
го порядка, допускающие разложения.
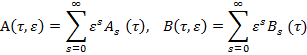
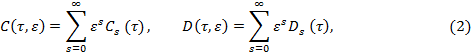
Вектор 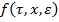 разлагается в ряд Тейлора в окрестности точки
разлагается в ряд Тейлора в окрестности точки  медленное время,
медленное время, 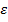 - малый положительный параметр. Предполагается, что функция
- малый положительный параметр. Предполагается, что функция 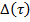 неотрицательна, т. е. удовлетворяет условию
неотрицательна, т. е. удовлетворяет условию
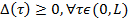 . (3)
. (3)
Как известно [1], при переменном запаздывании метод шагом может оказаться неприменим. В случае применимости, осуществление этого метода для уравнения вида (1) сопряжено со значительными трудностями, так как коэффициенты этого уравнения являются переменными. Поэтому возникает потребность в разработке метода, который бы позволял строить асимптотическое решение без использования метода шагов.
Такой метод впервые был предложен для линейных систем уравнений запаздывающего типа [2]. Позже этот метод был предложен для линейных дифференциальных уравнений с отклонением аргумента нейтрального типа.
В данной работе, в отличие от работы [2,3], рассматриваются так называемые критические случай [4] с применением обобщенной обратной матрицы, которые облегчают применение полученных результатов на практике.
Вначале рассмотрим вопрос построения формальных решений для системы (1), а затем исследуем асимптотические свойства полученных решений. При этом, под частным условимся понимать решение, соответствующее определенному корню уравнения
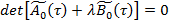 , (4)
, (4)
где 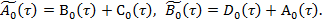
Пусть матрица 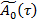 относительно матрицы
относительно матрицы 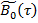 имеет один нулевой собственной значений, т. е. корни уравнений удовлетворяют условию
имеет один нулевой собственной значений, т. е. корни уравнений удовлетворяют условию
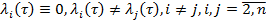 ,
, 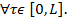 (5)
(5)
Тогда справедливо:
1. Теорема. Если матрицы 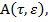
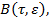
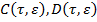 и скалярная функция
и скалярная функция 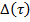 при
при 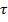 на сегменте
на сегменте 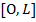 , а вектор
, а вектор 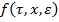 в области
в области 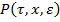 =P
=P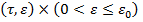 , где
, где 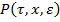 — некоторая область пространства переменных
— некоторая область пространства переменных 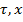 , принадлежат к классу
, принадлежат к классу 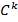 (для достаточно больших значений k), то система (1) имеет формальное частное решение, соответствующее нулевому корню уравнения (4) вида
(для достаточно больших значений k), то система (1) имеет формальное частное решение, соответствующее нулевому корню уравнения (4) вида
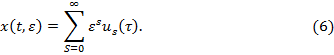
Доказательство. Для доказательства теоремы надо так определить коэффициенты ряда (6), чтобы вектор 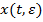 формально удовлетворял системе (1). Поставим вектор
формально удовлетворял системе (1). Поставим вектор 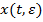 в систему (1) и получаем следующее уравнение
в систему (1) и получаем следующее уравнение
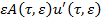 =
=

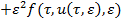
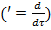 (7)
(7)
Разложим в формальные ряды по степеням параметра 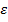 вектор
вектор 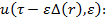
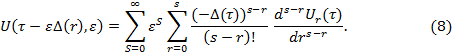
Прировняв в (7) выражения при одинаковых степенях параметра 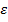 , получим следующую бесконечную систему уравнений для определения коэффициентов ряда (6):
, получим следующую бесконечную систему уравнений для определения коэффициентов ряда (6):
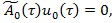 (9)
(9)
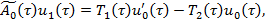 (10)
(10)
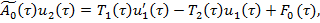 (11)
(11)
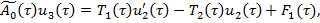 (12)
(12)
где
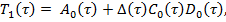
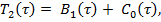
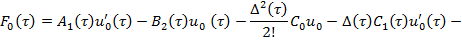
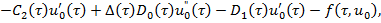
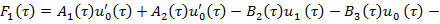
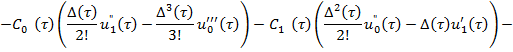

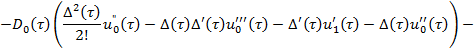
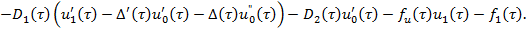
Рассмотрим первые из уравнений, полученные по системе (9)-(12). Уравнение (9), согласно [5], имеет решение вида
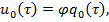 (13)
(13)
где 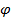 — собственный вектор матрицы
— собственный вектор матрицы 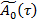 , в которой первые координаты равны единице, а остальные нулю,
, в которой первые координаты равны единице, а остальные нулю, 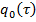 — на отрезке [0, L] отличная от нуля неизвестная функция определяется на следующем шаге.
— на отрезке [0, L] отличная от нуля неизвестная функция определяется на следующем шаге.
Уравнение (10), учитывая (13), запишем в виде
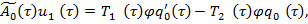 (14)
(14)
определитель система (14) равен нулю, т. е. 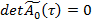 . В этом случае, как известно [2], для существования решения неоднородной системы (14), необходимо и достаточно, чтобы правая часть была ортогональна ко всем векторам, дающим решением соответствующей однородной союзной системы. Следовательно, условие ортогональности имеет вид
. В этом случае, как известно [2], для существования решения неоднородной системы (14), необходимо и достаточно, чтобы правая часть была ортогональна ко всем векторам, дающим решением соответствующей однородной союзной системы. Следовательно, условие ортогональности имеет вид
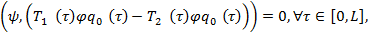 (15)
(15)
где 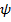 — вектор — решение однородной союзной системы, в котором
— вектор — решение однородной союзной системы, в котором 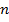 — ой координаты равно единица оставленный равный нулю.
— ой координаты равно единица оставленный равный нулю.
Из равенства (15), учитывая, что
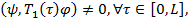 (16)
(16)
получаем относительно неизвестной функции 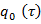 , однородное линейное дифференциальное уравнение первого порядка вида
, однородное линейное дифференциальное уравнение первого порядка вида
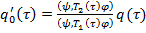 (17)
(17)
Интегрируя уравнение (17), определим неизвестную функцию 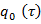 :
:
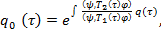 (18)
(18)
здесь постоянную интегрирования считаем равной единице.
Условие разрешимости для уравнения (14) имеет место, тогда из (14) определим неизвестный вектор 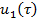 :
:
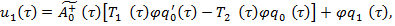 (19)
(19)
где 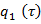 — неизвестная функция, определяющаяся на следующем шаге,
— неизвестная функция, определяющаяся на следующем шаге, 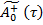 — обобщена обратная матрица к матрице
— обобщена обратная матрица к матрице 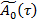 .
.
Имея в виду (19), уравнения (11) запишем следующим образом
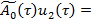
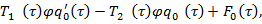 (20)
(20)
где
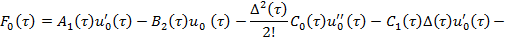
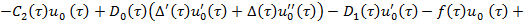
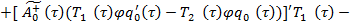
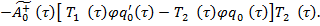
Условие разрешимости для уравнения (20) имеет вид
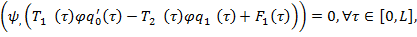
или
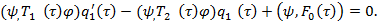 (21)
(21)
Таким образом, получаем относительно неизвестной функции 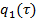 , линейное неоднородное дифференциальное уравнение первого порядка
, линейное неоднородное дифференциальное уравнение первого порядка
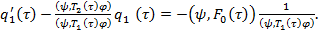 (22)
(22)
Интегрируя уравнения (22), получаем
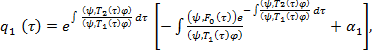 (23)
(23)
где 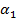 — постоянная интегрирования.
— постоянная интегрирования.
Условия (21) для уравнения (20) выполняются, тогда из него определим неизвестный вектор 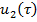 :
:
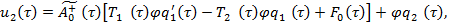 (24)
(24)
где 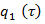 – неизвестная функция определяется на следующем шаге. Согласно уравнению (24), уравнения (12) запишем в виде
– неизвестная функция определяется на следующем шаге. Согласно уравнению (24), уравнения (12) запишем в виде
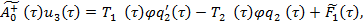 (25)
(25)
где
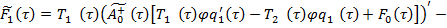
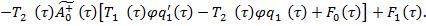
Условие (15) для уравнения (25) имеет вид
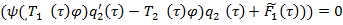 ,
, 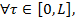
или
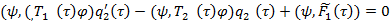 (26)
(26)
согласно условию (16), уравнение (26) запишется так:
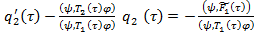 (27)
(27)
Решая уравнения (27). получаем
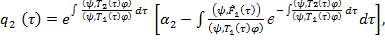 (28)
(28)
где 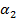 — постоянная интегрирования.
— постоянная интегрирования.
Учитывая выполнение условия (26) для уровнения (25), определим неизвестный элемент 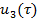 ряда (6):
ряда (6):
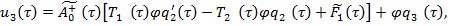 (29)
(29)
где 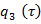 — как прежде, неизвестная функция определяется на следующем шаге.
— как прежде, неизвестная функция определяется на следующем шаге.
Очевидно, подобным способом можно последовательно определить все векторы 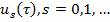 . Теорема доказана.
. Теорема доказана.
Выше изложены способы построения формальных частных решений системы (1), соответствующих определенному корню уравнения (4). Можно показать, что, при некоторых ограничениях, формальное решение асимптотических сходится к точному решению 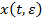 системы (1), т. е. норма разности между точным решением и его приближением -го порядка стремится к нулю при фиксированном
системы (1), т. е. норма разности между точным решением и его приближением -го порядка стремится к нулю при фиксированном 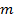 и
и 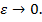
Под приближением -го порядка будем понимать вектор

Асимптотический характер формальных частных решений устанавливает.
Теорема 2. Пусть для системы (1) выполнены условия теоремы 1 и следующие:
1) Вектор 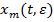 , определяемый равенством (30), на начальном множестве
, определяемый равенством (30), на начальном множестве 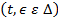 совпадает с точным решением системы (1)
совпадает с точным решением системы (1)
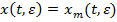 ,
, 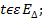 (31)
(31)
2) Функция 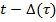 растет строго монотонно на отрезке [0,
растет строго монотонно на отрезке [0, ], причем
], причем
 (32)
(32)
3) 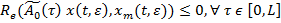 ; (33)
; (33)
4) для вектор — функция 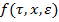 выполняются условия Лепщица с постоянной
выполняются условия Лепщица с постоянной 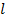 :
:
||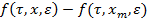 ||
||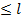 ||
||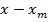 ||. (34)
||. (34)
Тогда существуют постоянные 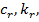 не зависящие от
не зависящие от 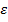 и такие, что для всех
и такие, что для всех 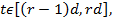 где
где 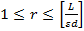
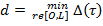 (35)
(35)
справедливы неравенства
||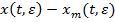 ||
||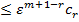 ;
;
||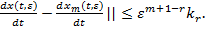
Литература:
1. Эльсгольц Л.Э, Норкин С. Б. «Введение в теорию дифференциальных уравнений с отклоняющимися аргументом». — М.: Наука, 1971. — 295 с.
2. Шкиль Н. И. «О некоторых асимптотических методах в теории линейных дифференциальных уравнений с медленно меняющимися коэффициентами»: Дис… доктора физ.-мат. наук. — Киев, 1968. — 420 с.
3. Фешенко С. Ф., Шкиль Н. И., Пидченко Ю. П., Сотниченко Н. А. «Асимптотические методы в теории линейных дифференциальных уравнений с отклоняются аргументом». — Киев. Наукова думка, 1981. — 296 с.
4. Васильева А. Б., Бутузов В. Ф. «Сингулярное возмущенные уравнения в критических случаях». — Изд. МГУ, 1978. -105 с.
5. Алишев А. «Решение нелинейных дифференциальных уравнений дробного ранга». ДАН Усср, сер. А, № 6, 1982, с 6–9.







