Проведено численное моделирование движения вязкой несжимаемой неизотермической жидкости в прямоугольной полости с учётом теплоотвода через внешнюю границу дна выемки. Получены гидродинамическая картина течения жидкости и температурные профили для твёрдой и жидкой фаз. Изучено влияние условий теплообмена на характер движения теплоносителя.
Ключевые слова: сопряжённый теплоперенос, гидродинамика, технологическая полость, вязкая несжимаемая неизотермическая жидкость, численное моделирование.
Интерес к исследованию конвективных течений c различными условиями теплообмена в полостях различных типов обусловлен широким прикладным значением проблемы. Большое количество теплотехнических устройств используются в энергетических установках и системах, производственных процессах различного уровня сложности. Необходимость изучения данных процессов обусловлена развитием таких энергоемких отраслей промышленности, как энергетическая, металлургическая, химическая и многих других [1–5].
В данной работе рассматривается нестационарное взаимодействие жидкости с открытой прямоугольной полостью (рис.1). Изучается процесс движения расплава металла в каверне с учётом теплообмена с её стенками и омывающей средой. Цель данной работы — исследовать гидродинамику и сопряжённый теплообмен при движении вязкой несжимаемой неизотермической жидкости в полости в условиях охлаждения внешней границы дна выемки. Ранее [6–8] были решены аналогичные задачи с условиями теплоизоляции на внешних границах полости.
Постановка задачи. Изучение описанного процесса проводилось с использованием математической модели на основе системы уравнений Навье-Стокса в переменных вихрь-функция тока, уравнения энергии, уравнения теплопроводности для материала полости с соответствующими начальными и граничными условиями
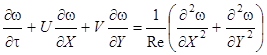 (1)
(1)
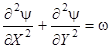 (2)
(2)
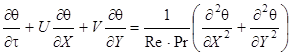 (3)
(3)
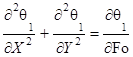 (4)
(4)
Система уравнений (1)-(4) сформулирована по аналогии с постановками задач в преобразованных переменных "ω-ψ" [9], применявшимися для моделирования процессов тепломассопереноса в условиях свободной и смешанной конвекций [10, 11] и интенсивных фазовых превращений [12, 13].
Здесь Fo — число Фурье; Re — число Рейнольдса; Pr — число Прандтля; 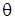 — безразмерная температура жидкости;
— безразмерная температура жидкости; 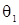 — безразмерная температура материала полости; X, Y — безразмерные декартовы координаты; U, V — безразмерные продольная и поперечная составляющая скорости движения жидкости соответственно; ω, ψ — переменные вихрь — функция тока.
— безразмерная температура материала полости; X, Y — безразмерные декартовы координаты; U, V — безразмерные продольная и поперечная составляющая скорости движения жидкости соответственно; ω, ψ — переменные вихрь — функция тока.
На нижней границе (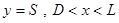 ) и боковой (
) и боковой (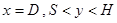 ) выставляется условие непротекания, прилипания, а также граничное условие четвёртого рода для уравнения энергии (задача решена в сопряжённой постановке).
) выставляется условие непротекания, прилипания, а также граничное условие четвёртого рода для уравнения энергии (задача решена в сопряжённой постановке).
Условия неразрывности тепловых потоков и непротекания заданы на линии симметрии (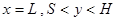 ). На участке выхода выставлялись условия «сноса» и «мягкое» граничное условие для скорости и температуры соответственно [9].
). На участке выхода выставлялись условия «сноса» и «мягкое» граничное условие для скорости и температуры соответственно [9].
На внешних границах полости заданы условия теплоизоляции, за исключением донной области (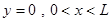 ), на которой принято граничное условие третьего рода (моделируется интенсивный теплообмен с внешней средой):
), на которой принято граничное условие третьего рода (моделируется интенсивный теплообмен с внешней средой):
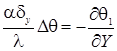 .
.
В граничных условиях и на рис.1 приняты следующие обозначения: x, y — размерные декартовы координаты; L — линейный размер полости по координате x; H — линейный размер полости по координате y; D — линейный размер стенки полости по координате x; S — линейный размер стенки полости по координате y; 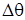 — разность безразмерных температур между внешней границей (
— разность безразмерных температур между внешней границей (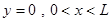 ) и окружающей средой; α — коэффициент теплоотдачи; λ — коэффициент теплопроводности; δy — толщина стенки по координате y; u, v — размерные продольная и поперечная составляющая скорости движения жидкости соответственно; T0, v0– начальные размерные значения температуры и скорости.
) и окружающей средой; α — коэффициент теплоотдачи; λ — коэффициент теплопроводности; δy — толщина стенки по координате y; u, v — размерные продольная и поперечная составляющая скорости движения жидкости соответственно; T0, v0– начальные размерные значения температуры и скорости.
Решена система уравнений Навье-Стокса в переменных функция тока-вихрь, урав-нение энергии и уравнение теплопроводности методом конечных разностей [9]. Разностные аналоги уравнений переноса и теплопроводности решены методом прогонки [9]. Уравнение Пуассона на каждом временном слое решалось методом последовательной верхней релаксации. Использовалась разностная схема второго порядка точности.
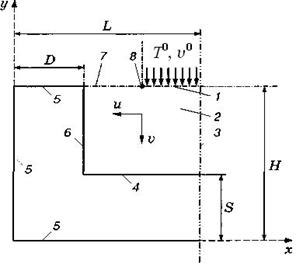
Рис. 1. Общая схема течения в полости и геометрия расчётной области (1–8): 1, 7 — проницаемые участки (участки затекания и выхода соответственно); 2 — гидродинамическая область; 3 — линия симметрии; 4,6 — внутренние поверхности; 5 — внешние поверхности; 8 — граница раздела между проницаемыми участками.
Вычисления выполнялись на равномерной и неравномерной разностных сетках. Оценка достоверности результатов численного моделирования проводилась проверкой консервативности использовавшейся разностной схемы аналогичным методом, применявшимся в [14, 15].
Анализ полученных результатов. В процессе проведения численного исследования рассматривалась жидкость разных типов (вода, расплавленный свинец, жидкая сталь, мазут) с широким диапазоном изменения динамического параметра Re и параметров модели. В данной статье представлены результаты математического моделирования описанных процессов для жидкой стали. На рис.2–4 приведены типичные результаты численных исследований.
Как следует из анализа установившегося поля течения для различных вариантов геометрических характеристик полости выделяется два этапа. К первому этапу относится движение жидкости от участка входа до нижней границы полости. На втором этапе движется жидкость от дна полости до выходного участка, образуя область возвратного течения с рециркуляционными зонами. Характерные области прямого и возвратного течения, соответствующие описанным этапам движения жидкости в выемке, отражены на рис.2.
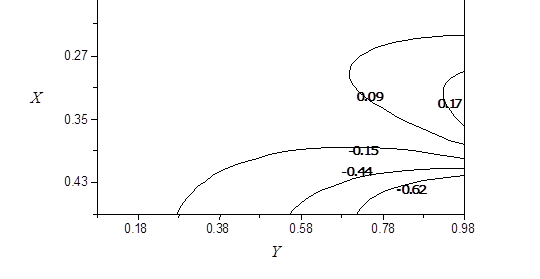
Рис. 2. Изолинии поперечной составляющей скорости в момент времени Fo=6,0∙10–2 при числе Re=500 и геометрическом отношении сторон полости L/H=1/2
Анализ полученных результатов показывает, что характер распределения поперечной составляющей скорости качественно сохраняется на первом этапе движения. На втором этапе происходит изменение характера распределения, обусловленное как возвратным течением жидкости, так и влиянием её динамических параметров и геометрических характеристик полости. С увеличением числа Рейнольдса
в условиях теплоотвода через нижнюю внешнюю границу (донную) профиль поперечной составляющей скоростив начальных сечениях полости становится более заполненным и близким к постоянному значению. Формируется два максимума прямого и возвратного течений, которые начинают смещаться (это хорошо видно при сравнении рассматриваемых профилей в условиях теплоизоляции внешних границ полости) вдоль координаты X в сторону боковой поверхности.
При движении жидкости к основанию выемки поперечная составляющая скорости падает в условиях роста продольной составляющей (рис.3). На возвратном этапе движения к выходному участку продольная составляющая скорости падает, а функция V от X начинает возрастать, что хорошо иллюстрирует физическое представление о природе протекающего процесса.
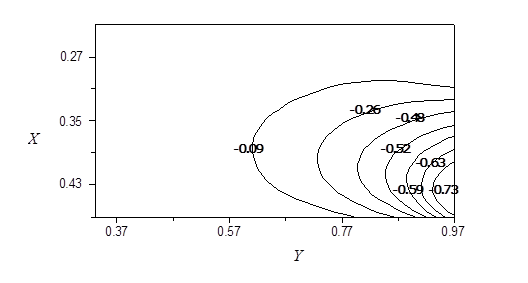
Рис. 3. Изолинии продольной составляющей скорости в момент времени Fo=6,0∙10–2 при числе Re=500 и геометрическом отношении сторон полости L/H=1/2
Из рис.2, 3 следует, что по мере приближения жидкости к основанию выемки поперечная скорость падает при возрастании продольной составляющей. На возвратном участке движения поперечная составляющая скорости начинает расти.
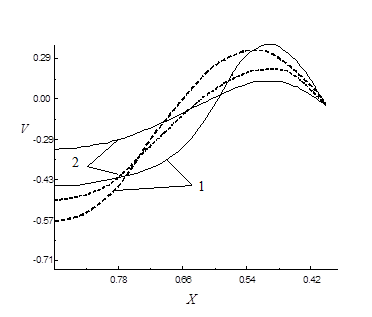
Рис. 4. Распределение поперечной составляющей скорости для разных размеров участка затекания в полость: 1) α=0.2α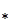 (сплошные линиии); 2) α=0.31α
(сплошные линиии); 2) α=0.31α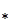 (штриховые линии). Кривые 1 соответствуют значениям поперечной составляющей скорости в сечении Y=0.69; 2- Y=0.37
(штриховые линии). Кривые 1 соответствуют значениям поперечной составляющей скорости в сечении Y=0.69; 2- Y=0.37
Рассматривалось влияние на характеристики течения длины входного участка (α). На рис.4 приведено распределение поперечной составляющей скорости для разных размеров входного участка: 1) α=0.22α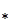 (сплошные линии); 2) α=0.38α
(сплошные линии); 2) α=0.38α (штриховые).
(штриховые).
Здесь α — обозначение полной длины проницаемого участка полости
— обозначение полной длины проницаемого участка полости 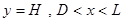 . Представленные кривые 1 и 2 соответствуют функции V(X) в сечениях Y=0.69 и Y=0.37. С увеличением длины входного участка максимальное значение поперечной скорости незначительно уменьшается на проницаемых участках полости, особенно это хорошо фиксируется в начальных сечениях. С уменьшением длины входного участка максимальное значение функции U(X) по сечениям начинает уменьшаться и меняется характер её распределения.
. Представленные кривые 1 и 2 соответствуют функции V(X) в сечениях Y=0.69 и Y=0.37. С увеличением длины входного участка максимальное значение поперечной скорости незначительно уменьшается на проницаемых участках полости, особенно это хорошо фиксируется в начальных сечениях. С уменьшением длины входного участка максимальное значение функции U(X) по сечениям начинает уменьшаться и меняется характер её распределения.
На рис.5 представлены распределения температуры в твёрдой и жидкой фазах в плоскости X, Y в момент времени Fo=6,0∙10–2 при Re=500, Pr=0.979 и геометрическом отношении сторон полости L/H=1/2. В условиях теплоотвода через внешнюю нижнюю поверхность полости характер распределения температуры в жидкой фазе по сечениям носит значительно более выраженный характер, чем в твёрдой.
Характер температурных распределений в жидкой и твердой фазах качественно сохраняется с изменением динамических параметров, размеров входного участка и геометрических отношений. Диапазон изменения температуры в условиях внешнего теплообмена для рассматриваемых процессов значительно увеличивается, что оказывает достаточно существенное влияние на формирование структуры течения жидкости.
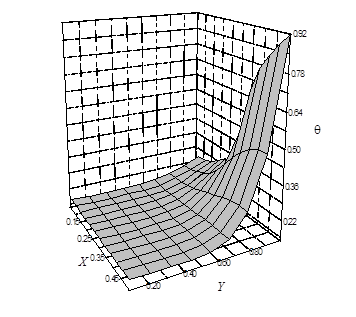
Рис. 5. Распределения температуры в твёрдой и жидкой фазах на плоскости X, Y в момент времени Fo=6,0∙10–2 при Re=500, Pr=0.979 и геометрическом отношении сторон полости L/H=1/2
Выводы:
Результаты численного анализа позволяют оценить влияние охлаждения внешней поверхности дна полости на условия теплообмена и гидродинамическую картину течения теплоносителя.
Проведённые исследования позволяют сделать вывод о возможности расширения области применения математического аппарата [6–8] для решения сопряжённых задач о конвективных течениях в открытых полостях c более сложными геометриями и условиями теплообмена на внешних границах.
Литература:
1. Рыкалин Н. Н., Углов А. А., Анищенко Л. М. Высокотемпературные технологические процессы. Теплофизические основы. — М.: Наука, 1985. — 172c.
2. Махнова Г. В., Рис В. В., Смирнов Е. М. Двумерная ламинарная свободная конвекция в полости, имеющей форму квадрата со скругленными углами// Свободная конвекция. Тепломассообмен при химических превращениях. Тр. Второй Рос. нац. конф. по теплообмену. — М.: МЭИ, 1998. — Т.3. — с.100–103.
3. Fedorov A. G., Viskanta R. Three-dimensional conjugate heat transfer in the microchannel heat sink for electronic packaging // J.Heat Mass Transfer.-2000.-№ 43.-p.399–415.
4. Krainov A. V. Conjugate heat exchange for a viscous incompressible fluid moving in a rec- tangular cavity under conditions non-uniformity phase characteristics // Proceedings of In-ternational Conference Conjugate problems of mechanics, computer science and ecology.- 2004.-p.302–303
5. Kuznetsov G. V., Sheremet M. A. Modelling of non-stationary heat transfer in closed area with a local heat source // J. Thermophysics and Aeromechanics.-2005.-v.12.-№ 2.-p.287- 295.
6. Крайнов А. В. Численный анализ сопряжённого тепломассопереноса и гидродинамики при движении вязкой несжимаемой жидкости в открытой полости в условиях вынужденной конвекции // Известия Томского Политехнического Университета. — 2003. — т.306.- № 2.-с.84–89
7. Kuznetsov G. V., Krainov A. V., Shvalova G. V. Conjugate heat exchange and hydrodyna- mics for a viscous incompressible fluid moving in a cavity with the consideration phase nonuniformaty characteristics // В мире научных открытий.- 2010.- № 6.1 (12).- с.119–122
8. Kuznetsov G. V., Krainov A. V. Conjugate heat exchange and hydrodynamics for a viscous incompressible fluid moving in a rectangular cavity // J. Applied Mechanics and Technical Physics.- 2001.- v.42.- № 5.- p.851–856.
9. Пасконов В. М., Полежаев В. И., Чудов Л. А. Численное моделирование процессов тепло- и массообмена. — М.: Наука, 1984. — 288 с.
10. Kuznetsov G. V., Sheremet M. A. Mathematical modelling of complex heat transfer in a rectangular enclosure // J. Thermophysics and Aeromechanics.-2009.-v.16.-№ 1.-p.119- 128.
11. Kuznetsov G. V., Sheremet M. A. New approach to the mathematical modelling of thermal regimes for electronic equipment // J. Microelectronics.-2008.-v.37.-№ 2.-p.131- 138.
12. Kuznetsov G. V., Strizhak P. A. 3D problem of heat and mass transfer at the ignition of a combustible liquid by a heated metal particle // J. Engineering Thermophysics.-2009.- v.18.-№ 1.-p.72–79.
13. Kuznetsov G. V., Strizhak P. A. The influence of heat transfer conditions at the hot particle-liquid fuel interface on the ignition characteristics // J. Engineering Thermo-physics.-2009.-v.18.-№ 2.-p.162–167.
14. Vysokomornaya O. V., Kuznetsov G. V., Strizhak P. A. Simulation of the ignition of liquid fuel with a local source of heating under conditions of fuel burnout // J. Physical Chemistry.-2011.- v.5.-№ 4.-p.668–673.
15. Kuznetsov G. V., Strizhak P. A. Heat and mass transfer at the ignition of a liquid substance by a single «hot» particle // J. Engineering Thermophysics.-2008.-v.17.-№ 3.-p.244–252.
16. Тарунин Е. Л. Вычислительный эксперимент в задачах свободной конвекции. — Иркутск: Изд-во Иркут.ун-та, 1990. — 225 c.
17. Самарский А. А., Вабищевич П. Н. Вычислительная теплопередача. — М.: Едиториал УРСС, 2003. — 784 с.







