В соответствии с программой федеральных государственных образовательных стандартов высшего профессионального образования (ФГОС ВПО) требования предъявляются не только к компетенциям, которыми должен овладеть выпускник в результате освоения образовательного курса, но и также к созданию необходимых психолого-педагогических условий, оптимальных для их формирования. В представленной статье автором рассмотрен вопрос об анализе таких условий, созданных в одном из педагогических вузов Дальнего Востока. В основу изучения были положены психологические представления студентов о математическом образовании, получаемых ими.
Ключевые слова: ФГОС ВПО; профессиональная подготовка будущих учителей математики; психолого-педагогические условия обучения
Психологические представления совокупного субъекта всегда отражают условия его бытия. Но прежде чем изложить представления молодых специалистов о математическом образовании в процессе их профессиональной подготовки, мы решили прокомментировать основные проблемы и психологическую сущность современного образования. Нам удалось найти новые подходы к оценке современного математического образования с точки зрения психологии. Особо импонирует идея Ареста М. Я. (Arest Michael), современного математика, доктора философии и психологии, проживающего сейчас в Израиле. Основные положения его теории легли в наше обоснование перспектив развития современного математического образования.
В настоящее время в системе образования продолжает господствовать процесс обучения, который осуществляется посредством субъектно-субъектного отношения «учитель-ученик» и проходит в возрастном развитии следующие стадии в процессе образования:
1) «родитель-ребенок» (возрастная категория от рождения до 3 лет). На этой стадии ребенок познает мир через познавательную среду, создаваемую родителями. Его интеллектуальный уровень определяется интеллектуальным потенциалом родителей. Психология познавательной деятельности определяется психологической подготовкой родителей;
2) «воспитатель-ребенок» (возрастная категория 3–6 лет). На этой стадии ребенок познает мир через познавательную среду, создаваемую детским садом. Его интеллектуальный уровень определяется интеллектуальным потенциалом воспитателя. Психология познавательной деятельности определяется психологической подготовкой воспитателя;
3) «учитель-ученик» (возрастная категория 6–17 лет). На этой стадии ученик познает мир через познавательную среду, создаваемую учителем. Его интеллектуальный уровень определяется интеллектуальным потенциалом учителя. Психология познавательной деятельности определяется психологической подготовкой учителя;
4) «профессор-студент» (возрастная категория 17–22 года). На этой стадии студент получает специализацию через познавательную среду, создаваемую профессором. Его интеллектуальный уровень определяется интеллектуальным потенциалом профессора. Психология познавательной деятельности определяется психологической подготовкой профессора.
Мы видим, что во всех случаях образовательная деятельность является обучающей деятельностью, определяемой такой парой как педагогическая деятельность и учебная деятельность. Возможны два способа организации педагогической деятельности:
1) лекционно-вербальный подход, психологической основой которого является принцип Ж. Пиаже (слова обрабатывают мышление). В этом случае педагог объясняет и добивается понимания вопросами «Это понятно?». Если он скрупулезно раскрывает содержание, то у учащихся возникает иллюзия понимания. Свое непонимание они обнаруживают потом в самостоятельной деятельности;
2) деятельностный подход, психологической основой которого является принцип Л. С. Выготского (самостоятельная деятельность порождает мышление). В этом случае педагог проблемно ориентирует ученика вопросами, формируя в нем умения к самопознанию. «Почему? Откуда это видно?», а также провокативным методом ложной информации. Если он активно раскрывает деятельность, то у учащихся возникает понимание изучаемого материала. В этом случае они способны задавать вопросы и активизировать образовательную деятельность.
То, что деятельностный подход Л. С. Выготского, построенный на диалектическом понимании мышления, более эффективен, чем подход Ж. Пиаже понято пока только в России, поскольку переводы Л. С. Выготского на иностранные языки смазывают содержательный смысл самого подхода. Работы Л. С. Выготского можно читать только на русском языке, а у западных психологов не всегда есть такая возможность.
Процесс обучения возникает в то время, когда информация не является массовой. В этом случае требуется источник информации, который и создает образовательное развитие. Поэтому процесс обучения начинается тогда, когда ребенок готов к восприятию информации. Ф. Энгельс отмечал, что пространственные материальные формы и количественные отношения между ними составляют основу математики. Понятно, что пространственные материальные формы могут иметь разное предназначение, поэтому теория отражения В. И. Ленина четко обозначает характер процесс познания, которая выдвигает два положения:
1) процесс познания — это процесс логического отражения реальной действительности;
2) процесс познания направлен от живого созерцания к абстрактному мышлению.
Однако В. И. Ленин не только не указал логические средства отражения, но и не раскрыл формы абстрактного мышления. Владея историей развития математического знания от древности до наших дней (филогенез математического знания) В. И. Ленин «снял» процесс этого развития в форме математических отношений, определив для каждого отношения тройку (логическое средство; логический способ; логическую форму). Следует отметить, что впервые задачу построения математики как системы развивающегося знания поставил В. В. Агеев, им были найдены те математические отношения, которые продвигали вперед интеллектуальное развитие социума. После этого была высказана гипотеза о соотнесении (но не отождествлении!) филогенеза математического знания с онтогенезом интеллектуального развития личности. Оказалось, что математические отношения найденные учёными, обладают следующими свойствами:
1) их освоение составляет содержательный смысл познавательного развития;
2) указанные отношения применимы на любом этапе возрастного развития, начиная с рождения ребенка;
3) движение от одного отношения к другому вызывает подлинное интеллектуальное развитие, поскольку напрягает гипофиз в поисках нового логического средства отражения.
Раскроем более подробно теорию М. Я. Ареста «Построение диалектической логики на базе теории множеств», а также его личные впечатления его как школьника и студента. Он писал о том, что получив высшее математическое образование, пришел к тому, что изучение математики проходит бессистемно. Начиная наблюдать за этим еще в школе, он закрепил это представление уже в университете. Тут следует отметить еще тот факт, что математическое образование на всей планете строится на принципе метафизического идеализма. Содержательной основой такого принципа является подача логических форм математических объектов без интерпретации содержательного смысла этих объектов. Такой способ изучения математики М. Я. Арест мысленно назвал «логическим хламом» и отказался принимать на веру все математические факты. По его мнению, ни одна из математических книг не пыталась донести до читателя содержательный, жизненный смысл того, что она предлагает. Поэтому впервые идею дифференциального и интегрального исчисления он понял не в университете при изучении математического анализа, а при чтении книги К. Маркса «Математические рукописи».
Именно К. Маркс открыл М. Я. Аресту диалектический смысл математического знания. Дальше он использовал в своем самообразовании (сохраненное от традиционного математического образования) природное диалектическое мышление и построил новое представление о математике, как об общей теории развивающихся структур. Теперь владея принципом развития, как методом построения фактор множества по заданному отношению (математический метод построения нового качества) и принимая за базу пространственные материальные формы, М. Я. Арест без труда смоделировал те познавательные уровни, которые общество прошло в своем интеллектуальном развитии: сенсорный; образный; символический; понятийный. Таким образом, было подтверждено утверждение В. И. Ленина о том, что теория познания, диалектика, диалектическая логика — это синонимы.
На основе этого М. Я. Арест изучил структуру интеллекта с целью описать процесс мышления. Он отмечает, что в традиционном математическом образовании под интеллектом понимается способность адаптироваться к восприятию логических форм, а под развитием логического мышления искусство манипулировать указанными логическими формами. Что касается математического развития, то при этом понимается движение в математическом знании от одного объекта к другому по мере возрастного развития. Понимая под математическим развитием движение от одного математического отношения к другому, М. Я. Арестом в соавторстве с Т. Акбашевым была опубликована работа [2], которая прошла без внимания и откликов со стороны педагогов и психологов. В этой работе авторы представляли не только математическое развитие, но и связывали его с познавательным развитием. С этой целью моделировался процесс познания содержания как развивающаяся структура математических отношений. В другой работе [3] указанные идеи доводились то технологического воплощения посредством системы заданий, формирующих педагогическую деятельность. Тем не менее, опубликованные результаты не вооружили воспитателей детских садов и учителей из-за того куцего математического образования, которое они получили. Совершенно очевидно, что чем сложнее внутренняя организация содержания объекта, тем более точными должны быть средства его изучения. Если для математического образования инженера-механика было нужно дифференциальное и интегральное исчисление (диалектический аппарат моделирования механического движения), то для математического образования педагога и психолога нужен более совершенный аппарат, которым является общая теория развивающихся структур, построенная М. Я. Арестом.
Только математическое образование поможет не только учителям математики, но и психологам так организовать процесс базового образования, что он приведет к процессу саморазвития субъекта. Математическое образование в его новом понимании становится необходимым инструментом познания в любой деятельности. Именно математическое образование позволит перейти от процесса обучения к процессу самопознания. Необходимо пересмотреть всю концепцию математического образования, которая была и остается психологически некорректной. М. Я. Арест проанализировал содержание математического образования и выявил его недостатки. Сложность в изменении концепции состоит в том, что она знаменует подлинную логическую революцию в виде перехода от логики Аристотеля (формальная логика) к логике Г. Гегеля (диалектическая логика, которая адекватна природному мышлению).
Различные попытки в совершенствовании обучающей деятельности уже обречены в условиях сегодняшних информационных технологий (доступность массовой информации). Переход от обучающей деятельности к познавательной знаменует новый смысл математического образования, в котором математика становится теорией познания. М. Я. Арест не только создал альтернативную методологию, но и обеспечил ее технологическое воплощение, построив базовое образование на игровой основе.
М. Я. Арестом была детально разработана концепция игрового образования как средство самопроектирования познавательной деятельности субъекта в математическом образовании. На идею игрового образования автора навел ныне покойный мурманский режиссер В. Штернберг. Но его идея относилась к школе начального развития: создание настольной образовательной игры. Взяв эту идею за основу, М. Я. Арест разработал теорию игрового образования в виде следующей последовательности: образовательная игрушка, образовательная настольная игра, образовательная компьютерная игра. Были определены ступени базового образования:
1) родительская школа;
2) школа начального развития;
3) школа самоопределения личности, также установлены видовые формы игрового образования для каждой ступени. Возник принципиально новый по качеству игровой мир.
На каждой ступени базового образования игровое образование имело собственные цели:
1) родительская школа была предназначена для активного развития всех сенсорных каналов восприятия и при этом активно задействовалась работа с подсознанием (при условии закрытых глаз);
2) школа начального развития формировала с помощью тех же отношений первичные экономические навыки, навыки чтения и письма, навыки рисования и музицирования;
3) школа самоопределения личности формировала профессиональную ориентацию.
В игровой системе автора (М. Я. Арест) получили особое значение электронные игрушки, построенные на микропроцессорной основе. Они стали первым познавательным инструментом. Другой смысл получили и различные конструкторы: они стали образным аналогом подлинного конструирования и потребовали более серьезного отношения к проектированию детских конструкторов. Что касается компьютерных игр, то они должны были проектироваться старшими школьниками для младших. Указанная игровая система образования исключила процесс обучения и обучающую деятельность. Игровая форма стала средством самопроектирования познавательной деятельности. Игровая познавательная деятельность выводила ученика на саморазвитие.
Применение игровых методов в образовательных системах не новшество, однако на практике идет разрыв между обсуждением данных методов с применением в практике обучения школьников и студентов. Неприменение игровых методов в процессе образования снижает учебную мотивацию как студентов, так и школьников. В оценке состоянии математического образования в России мы решили проанализировать условия современной математической подготовки студентов будущих учителей математики (математическое педагогическое образование) в сравнении с профподготовкой «студентов-статистиков» (математическое экономическое образование).
Мы исходили из того, что представления человека отражают условия его бытия, таким образом, субъективные представления студентов будут отражать условия их математического образования на современном этапе, при этом следует отметить, что обучение в университете осуществляется по существующим образовательным стандартам системы образования России. Испытуемые студенты получили задание продолжить предложение: «По-моему мнению современное математическое образование…». Результаты обрабатывались с помощью метода контент-анализа и методикой, предложенной Б. А. Еремеевым. Массив слов статистически обработан ранговой корреляцией Ч. Спирмена в программе «Статистика 6.0»
На рис. 1 изображена корреляционная плеяда, отражающая представления студентов-«математиков» о состоянии математического образования в России.
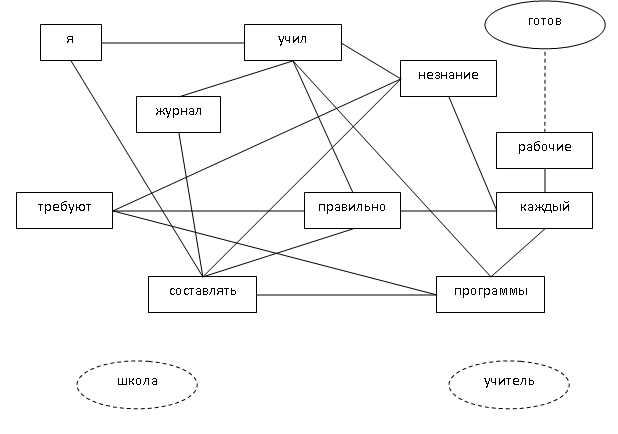
Рис. 1. Корреляционная плеяда, отражающая субъективные представления студентов «математиков» о состоянии математического образования в России (общий массив слов — 654)
Из рисунка 1 мы видим, что одной из естественных категорий выделилось слово «готов», которое обозначает «сделавший все необходимые приготовления, такой которые может что-нибудь предпринять или с которым может что-нибудь произойти, окончательно сделанный, годный к употреблению» (Толковый словарь русского языка С. И. Ожегова, Н. Ю. Шведовой, 2000). В представлениях будущих учителей математики «готов» приобретает обратную характеристику, которая отталкивается от естественной категории и приобретает отрицательное семантическое значение. Группа слов-интерпретаторов представляет нам двойственную ситуацию. С одной стороны, это человек, который «учился правильно, в соответствии с требованиями составлять программы», «учился правильно заполнять журнал». С другой стороны, во всей связке слов так или иначе присутствует слово «незнание», положительно коррелирующее с остальными, что порождает некий парадокс «учили незнание». В качестве естественных категорий также выделились слова «школа», которое согласно Толковому словарю обозначает «учебно-воспитательное учреждение, здание такого учреждения; выучка, достигнутый в чем-нибудь опыт, а также то, что дает такую выучку» и «учитель», обозначающее «лицо, которое обучает чему-нибудь, преподаватель; глава учения, человек, который учит чему-нибудь» (Толковый словарь), которые имеют нулевую связь с остальными словами. Складывается интересная интерпретация выпускниками своей профессиональной подготовки. Получается, то, чему их обучали ни коем образом не связано ни со школой, ни с учительством вообще.
На рис. 2 изображена корреляционная плеяда, отражающая представления студентов «статистиков». В плеяде обнаружены четыре цепочки слов, из которых две связаны между собой, а именно цепочки слов с естественными категориями «математическое» и «уровень», остальные цепочки слов с естественными категориями «мне» и «образование» выстроились автономно. Таким образом, в плеяде выделилось условно четыре характеристики состояния современного математического образования в отражении студентов «статистиков».
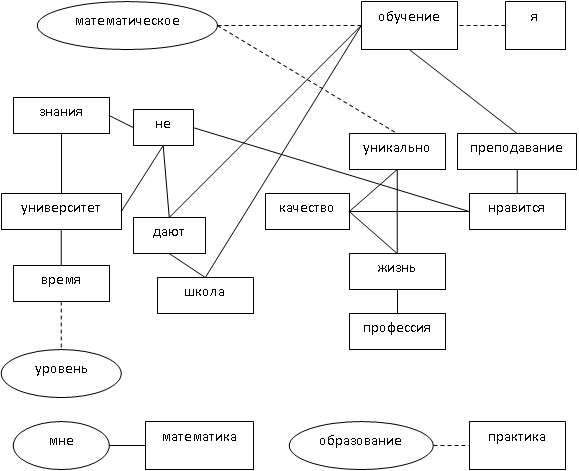
Рис. 2. Корреляционная плеяда, отражающая субъективные представления студентов «статистиков» о состоянии математического образования в России (общий массив слов — 248)
Со словом «мне», которое обозначает местоимение «я» в форме принадлежности, положительно связана наука «математика», что подчеркивает личностный смысл этой науки для студентов, данная наука им нужна, она напрямую связана с их профессиональными интересами.
Вторая цепочка слов обнаружила отрицательную корреляцию между словами «образование» и «практика», что указывает на то, что получаемое образование студентами сложно применимо на практике, особенно в условиях их профессиональной деятельности. В текстах было много эмоциональных высказываний после прохождения ими практики в отделе статистики при администрации города, диагностическом медицинском центре и пр. Многие студенты указывали на то, что им приходилось вновь осваивать математику и мат. статистику на рабочем месте, и не было ничего общего с полученным образованием в стенах университета.
Третья цепочка слов от естественной категории «уровень» имеет более сложную структуру, согласно толковому словарю русского языка «уровень» означает степень величины, развития и значимости чего-либо. Данное слово отталкивается от исходящей от него цепочки группы слов-интерпретаторов. Это приобретает обратный смысл, «время» не определяет «уровень» математического образования, «знания» «не» «даются» в «школе», а также «не» в «университете». Кроме этого частица «не» связывает данную цепочку слов с другой цепочкой слов-интерпретаторов, так складывается следующий смыл — «не нравится преподавание и обучение», а слово «обучение» связано с цепочкой слов «дают» и «школа». Таким образом, в представлениях студентов «статистиков» школа связана с процессом обучения, а университет с процессом преподавания, однако как не назови эти педагогические процессы, они не обеспечивают достойный уровень математического образования.
Четвертая цепочка слов с естественной категорией «математическое» отталкивается от слов «обучение» и «уникальное», этого следует, что все уникальное и процесс обучения не связаны с математической областью. Кроме этого местоимение «я» отталкивается от слова «обучение», студенты фактически признаются, что они не учатся. Однако «не математическое» образование «уникально», определяет «качество» «жизни», которое связывается студентами с получаемой «профессией», а упоминаемое ими «качество» в свою очередь связано с «преподаванием» и «обучением», которое им «нравится». То есть студенты разделяют образование в университете в целом и математическое образование, получается, что всё «математическое» как таковое отсутствует, а существует просто система образования.
Таким образом, мы видим, что студенты факультета технологии, экономики и дизайна не обнаруживают достойный уровень математического образования как в школе, так и в университете, причиной чего является собственное отрицательное отношение к обучению, они не хотят учиться и считают, что образование невозможно применить на практике, однако математическая наука приобретает для студентов личностный смыл в процессе ее применения на рабочем месте, в профессии статистика.
Парадоксальная ситуация сложилась с профессиональной подготовкой учителей математики, из плеяды четко выделилась их неготовность к профессии учителя. С одной стороны они готовы применять математическое образование, но не связывают его со школой и профессией учителя математики. Здесь явно у студентов отсутствует личностный смысл труда учителя математики.
Полученные нами результаты исследования показывают, что в процессе профессиональной подготовки студентов в области математического образования, следует не только транслировать математические знания, а связывать их с будущей профессией студентов, показывая им ситуации по их применению. Нельзя также забывать про профориентационную работу школ, которая готовит школьников психологически к выбору будущей профессии. Однако сейчас мы можем констатировать факт о разрыве связи между школами и вузами, современная профориентация построена на количественном подходе, какие предметы школьники в состоянии сдать, на такие направления образования они и делают выбор, то есть у них полностью отсутствует смыслообразующая составляющая своего выбора будущей профессии. Это приводит к тому, что математическое образование проходит формально, и студентам на практике в учреждениях приходится заново осваивать некоторые аспекты профессиональной подготовки и учиться самим применять свою математическую подготовку на практике.
Устные собеседования со студентами факультета информационных технологий, математики и физики показали, что при изучении методики преподавания математики в школе их обучают устаревшим игровым методам в преподавании математики школьникам. Таким образом, студенты «математики» ощущают отсталость и недоступность математического образования в плане практического применения. Современные математические книги по курсу высшей математики написаны очень сложным символическим языком, все, что остается в жизни человека, это умение оперировать числами, а алгебраические и тригонометрические формулы, и геометрические идеи — вылетают из головы и не применяются в жизни, что утрачивает весь смысл математического образования. Мы сталкиваемся с утратой смыслов у студентов-математиков, которые уже в своей профессиональной деятельности при преподавании математики в школе не могут передать смысл математического образования последующим поколениям.
Литература:
1. Арест, М. Я. Качественно новый подход к образовательной деятельности (31.08.2012). — Источник. [Электронный ресурс]. URL: http://ru.scribd.com/doc/104549682 (дата обращения 17.03.2015).
2. Арест, М. Я. Концепция базового математического образования в непрерывном образовании / Т. Акбашев, М. Я. Арест. — 2012. — Источник. [Электронный ресурс]. URL: http://ru.scribd.com/doc/104550921 (дата обращения 21.01.2015).
3. Арест, М. Я. Что изучает математика. — 2012. — Источник. [Электронный ресурс]. URL: http://ru.scribd.com/doc/103698154 (дата обращения 21.01.2015).
4. Логвинов, И.Н. 10 избранных лекций по педагогической психологии / И. Н. Логвинов, С. В. Сарычев. — Источник. [Электронный ресурс]. URL: http://vashpsixolog.ru (дата обращения 21.01.2015).
5. Сергеева, Т. Ф. Актуальные проблемы школьного математического образования /Т. Ф. Сергеева // Математика и математическое образование: материалы международной конференции «Proceedings of the Forty First Spring Conference of the Union of Bulgarian Mathematicians Borovetz», April 9–12, 2012. — С. 107–112.
6. Шакирова, Р. Г. Структура и уровни психологической готовности учителя к профессионально-педагогической деятельности. — Источник. [Электронный ресурс]. URL: http://childpsy.ru/dissertations/id/20108.php (дата обращения 18.12.2014).







