В данной статье рассматривается возможность применения сетей Петри для симулятора дорожно-транспортных ситуаций. Приведён анализ различных вариантов сетей Петри и архитектура моделей на их основе для верификации действий водителя согласно правилам дорожного движения.
Ключевые слова: сети Петри, цветная сеть Петри, вложенные сети Петри, правила дорожного движения.
На сегодняшний день основным методом проверки теоретических знаний Правил дорожного движения (ПДД РФ) учеников-водителей в ГАИ является тестовая форма. В её основе лежит заранее составленные вопросы с изображениями перекрёстков или каких-то дорожных ситуаций, а также список вариантов ответов. Однако, такой способ имеет ряд значительных недостатков, которые напрямую сказываются на навыках вождения у начинающего водителя.
Самым важным фактором является разница в подходах применения выученных правил водителем при сдаче теоретического экзамена и практического экзамена, непосредственно за рулём автомобиля. Эта разница заключается в том, что вопросы представляют собою набор статических ситуаций и не проверяет способность ученика-водителя быстро принимать решение в реальном времени. Такие задания не учитывают изменяющиеся факторы, которые возникают на дороге во время совершения различных манёвров и дают избыточное время на размышление над вопросом, чего в реальных условиях быть не может.
Одним из вариантов решение такой проблемы — это внедрение новой формы проверки знаний в виде компьютерного моделирования дорожных ситуаций и их симулирования в реальном времени в графическом трёхмерном представлении. При помощи такого подхода возможно конфигурация ситуаций различной сложности, с активными участниками дорожного движения, знаками и светофорами. При этом ученик-водитель, виртуально управляя автомобилем за компьютером в реальном времени, должен проехать смоделированное задание. В течение всего задания, действия водителя записываются, и в конце по ним происходит верификация согласно ПДД.
В качестве математического аппарата для моделирования дорожных ситуаций и дальнейшей их верификации предлагается использование сетей Петри. В сетях Петри моделирование осуществляется на событийном уровне [1]. Каждое событие (или переход) определяется на какие позиции (состояния) оно влияет и каким позициям оно предшествовало. В таких позициях могут находится фишки (маркеры), способные вместе со срабатыванием переходов перемещаться по сети. Срабатывание переходов в такой модели описывает поведение её системы. По результатам анализа выполнения системы возможно заключить в каком состоянии находилась она и какие состояния при этом не достижимы. Сеть Петри может осуществить необходимый уровень абстракции для данной задачи и верификации на основе собранных записей (логов) действий водителя.
Могут существовать разные подходы к реализации данной задачи с помощью сетей Петри. Одним из возможных вариантов может являться применение классических сетей Петри. Главной проблемой реализации является, каким образом будут определены дорожные правила с реальной ситуацией и как они будут верифицированы. Модель должна содержать покрывающий граф всех возможных действий водителя для заданной модели дороги. В контексте классических сетей Петри для решения данной задачи стоит допустить, что позиции могут быть двух видов. Первый вид отвечают за части дороги, а второй вид содержит информацию о нарушениях. Однако, такой способ избыточно усложняет структуру модели. Для этого стоит рассмотреть пример проезда нерегулируемого перекрёстка с пересечением равнозначных дорог (Рис 1).
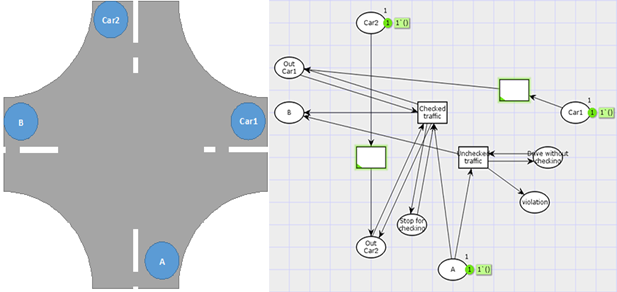
Рис. 1. Графический вид равнозначного перекрёстка со встречным трафиком и его модели в представлении классической сети Петри
На представленной схеме изображено задание для ученика-водителя, в котором ему необходимо совершить левый поворот и, таким образом, попасть из позиции А в позицию B,учитывая помеху справа (Car 1) и встречный трафик (Car 2). Рассматривая модель сети Петри данной ситуации для проведения верификации действий водителя, необходимо проверить уступает ли ученик дорогу встречному автомобилю. Для этого в модель внесены дополнительные позиции Stop for checking и Drive without checking для проверки дорожных правил. Стоит отметить, что в этой модели не учтены другие правила, такие как включение сигнала поворота или же знаки проезда перекрёстка. Включение этих факторов сильно усложнило бы модель, так как потребовало создания дополнительных позиций для покрытия всех действий водителя в рамках данной дорожной ситуации.
Для разделения фишек и разных смысловых типов позиций можно рассмотреть вариант использования расширенных сетей Петри в формате цветных сетей Петри [2]. В цветных сетях Петри фишка фактически является объектом с набором параметров. Каждая позиция может содержать только один тип фишки. На основании функций дуг и условий переходов осуществляется их срабатывание, а во время исполнения значения в фишке могут меняться.
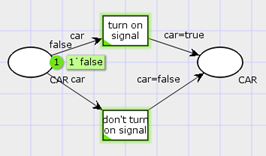
Рис. 2. Использование фишки с булевым типом, отражающее использование сигнала поворота
На рисунке 2 изображён элементарный пример использования цветных сетей Петри в контексте задачи. В данной модели представлены две позиции с типом фишек CAR, которые являются начальной и конечной точкой поворота соответственно. Фишка этого типа содержит одно значение булева типа, которое отражает информацию о включённом сигнале поворота. Однако, данное расширение не решает проблему разделения позиций действий водителя и структуры дороги, а только предлагает содержать в более удобном виде информацию о нарушениях и свойствах автомобиля.
Наиболее подходящим видом сетей Петри для применения к реализации моделирования структуры улицы и автомобиля с учётом вышеописанных особенностей могут служить вложенные сети Петри [3]. Вложенная сеть Петри — это расширенная цветная сеть Петри, в которой фишки задающие маркировку сети, сами являются сетями Петри. Такие сети обладают автономным поведением и взаимодействуют друг с другом и с основной сетью.
Для данной задачи следует рассматривать двухуровневую вложенную сеть Петри [4]. В таком варианте улица может быть представлена через системную сеть, а элементарная сеть состояла бы из состояний действий водителя. Структура сети перекрёстка может базироваться на принципах связанных логически секторов дороги. В качестве примера рассмотрим равнозначный перекрёсток (Рис. 3).
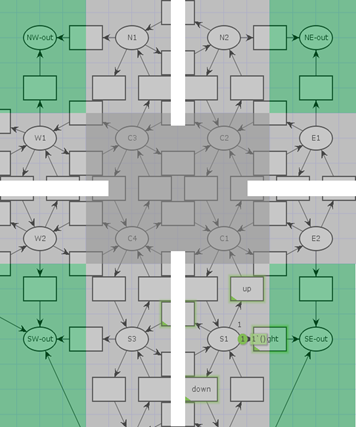
Рис. 3. Представление равнозначного перекрёстка в сети Петри
Каждый такой сектор дороги является позицией в системной сети во вложенной сети Петри. Для этого следует принять во внимание факторы, которые отражают физическую составляющую каждого такого дорожного сектора (позиции) модели в сети Петри:
- Каждая позиция в сети имеет не больше 4-ых соседних позиций с каждой стороны, в контексте дороги — это по соседнему сектору с каждой стороны света (север, юг, запад, восток)
- Каждая позиция имеет по два перехода для каждого направления с дугой размерностью равной единицы
- Каждая позиция может содержать фишку, которая является элементарной сетью модели автомобиля
- Движение автомобиля по секторам дороги преобразуются в срабатывание переходов между соответствующих позиций
В результате, модель дороги, разбитой по таким секторам будет представлять собою «мозаику» положений и переходов сетей Петри, при этом в симуляторе каждый такой сектор имеет реальные физические размеры. В представленном примере (Рис. 3) сеть покрывает все возможные движения автомобиля в границах дороги. Позиции сети имеют переходы только с соседними позициями. Так, в позиции S1 содержит фишку (представляемую как автомобиль), которая активирует переходы (up, down, right, left) только в соседние позиции (сектора дороги). Следовательно, при движение на север, сработает переход up и фишка попадёт в позицию С1 — в центральную часть перекрёстка.
Во время симуляции возможен вариант, когда ученик-водитель может выехать за пределы проезжей части дороги. В этом случае фишка, представляющая автомобиль, попадает в финитную позицию. Такая позиция не имеет исходящих дуг и в физическом смысле это означает, что автомобиль попал в аварию и симуляция окончена. Также стоит отметить, что при реализации данной модели необходимо установить для каждой позиции свойство о том, разрешён ли въезд автомобилю на данную секцию или нет, относительно установленных знаков проезда перекрёстка.
Модель автомобиля представлена элементарной сетью вложенной сети Петри. Она должна включать набор действий водителя и основные свойства автомобиля относительно правил дорожного движения (Рис 4).
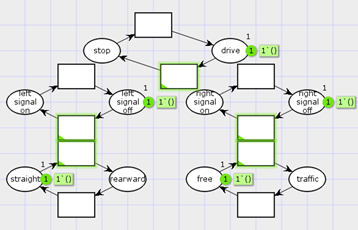
Рис. 4. Структура элементарной сети Петри для автомобиля
На диаграмме модели представлены пять независимых групп состоящих из двух позиций. Каждая такая группа представляет собой свойство автомобиля с дискретным значением. На схеме это группы, отвечающие за движение, направление, включение сигналов поворота и наличия помехи в виде другого автомобиля. Также, стоит упомянуть, что исходя из определения вложенных сетей Петри, некоторые переходы могут быть синхронизированы с переходами системной сети дороги, в данном случае это группа позиций присутствия других участников движения на дороге.
Верификация действий ученика-водителя происходит на основе основных собранных данных, которые включают в себя позицию автомобиля относительного секторов дороги, события включения сигналов поворота и информацию о наличие трафика. Последовательность записанных событий выполняется как на системной так и на клиентской сети Петри. В результате, чего происходит анализ каждого шага и действия ученика-водителя по свойствам позициям сети.
Дальнейшим этапом развития данного подхода может служить добавление вложенных сложных участков дорог в системную сеть. Идея такой реализации заключается в том, что позиция может быть представлена подсетью Петри, в которой содержится модель поведения автомобиля согласно дорожному знаку, применяемому в этой секции. Также, следующим вариантом развития модели на основе вложенных сетей Петри является валидация самих тестовых вопросов согласно ПДД. В этом случае, система сможет проверить на наличие ошибок и противоречий в дорожных знаках на этапе проектирования данных заданий. Таким образом, использование в качестве формального метода вложенных сетей Петри предоставляет новые возможности моделирования дорожно-транспортных ситуаций и верификации правил движения.
Литература:
1. H. Kubátová. «Modeling by Petri Nets», Czech Technical University in Prague Acta Polytechnica, vol. 45, No. 2, 2005.
2. K. Jenson, «Colored Petri Nets and The Invarient-Method». Computer Science Department AARHUS University, Denmark. Aug. 1980.
3. K. Hee, A. Serebrenik, I. A. Lomazova, N. Sidorova, O. Oanea, M. Voorhoeve «Nested nets for adaptive systems». Program Systems Institute of Russian Academy of Science, Pereslavl-Zalessky, Russia.
4. Ломазова И. А. Вложенные сети Петри: моделирование и анализ распределенных систем с объектной структурой. — М.: Научный мир, 2003. — 208 c.







