Добыча и подготовка нефтяного сырья неразрывно связана с такими процессами как увеличение давления в пластовой зоне с помощью нагнетательных водных скважин, смешение нефти с водой при ее поднятии, обессоливание нефти с помощью промывки водой. На сегодняшний день водонефтяные эмульсии являются естественным продуктом инженерного процесса получения жидких углеводородов. Совершенствование процессов разделения (демульсификации, обезвоживания) водонефтяных эмульсий — одна из актуальных научно-производственных задач нефтяного хозяйства, решение которой способно принести значительный экономический эффект, повысить надежность промыслового и магистрального транспорта нефти, улучшить качество нефтепродуктов [1, c. 157].
В настоящее время в качестве физического принципа разделения водонефтяных эмульсий в промышленных масштабах на объектах нефтедобычи используется эффект электрофореза (движения заряженных частиц вдоль линий напряженности электрического поля) и диэлектрофореза (движения поляризованных веществ в сторону наибольшей напряженности электрического поля).
Наибольшее распространение получила конструкция электродегидратора, при которой водонефтяная эмульсия подвергается воздействию однородного электрического поля плоского конденсатора (Рис. 1).
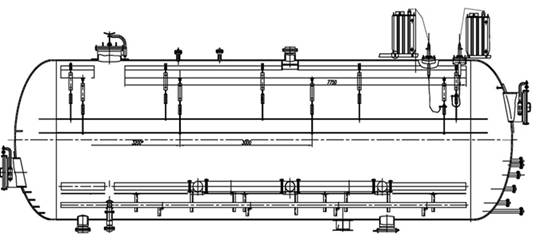
Рис. 1. Схема типового цилиндрического электродегидратора горизонтального исполнения [2, с. 67].
При этом, в межэлектродном пространстве заряды в каплях воды приходят в движение (электрофорез), концентрируются на противоположных концах капель и вытягивают каплю вдоль линий электрического поля. Заряды, сконцентрированные на концах капель, создают мелкомасштабную неоднородность электрического поля, которая, в свою очередь, создает условия для взаимного притяжения капель под действием сил диэлектрофореза. Основной физический механизм, приводящий к взаимному слиянию капель (диэлектрофорез), при такой конструкции электродегидратора, реализуется лишь при небольших расстояниях между поляризованными каплями [3, c. 67].
Интенсификация электрокоалесценции капель возможна при расширении масштаба действия эффекта диэлектрофореза, а именно, за счет использования изначально неоднородного электрического поля. В неоднородном электрическом поле за счет диэлектрофореза капли воды, даже при значительных расстояниях между другими каплями, будут стремиться двигаться в сторону наибольшего возрастания напряженности электрического поля. Таким образом реализуется дополнительный сближающий механизм, который будет приводить к сокращению расстояния между каплями воды и интенсификации их слияния.
Основная цель данной работы состоит в составлении алгоритма к расчету сложной конфигурации неоднородного электрического поля, возникающего в электродегидраторах с несимметричной конфигурацией электродов. Именно наличие неоднородного электрического поля во всем объеме электродегидратора является необходимым условием к появлению сил диэлектрофореза.
Основным рабочим органом современных электродегидраторов является симметричный плоский конденсатор, модуль напряженности поля внутри которого однозначно определяется напряжением на электродами и расстоянием между ними, а направление поля строго перпендикулярно электродам (Рис. 2).
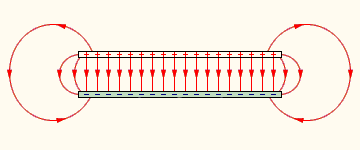
Рис. 2. Схематичное изображение поля симметричного плоского конденсатора. Слева и справа от пластин — изображение «краевого эффекта» — неоднородности электрического поля
В практике расчетов симметричных плоских конденсаторов как правило пренебрегают так называемыми «краевыми» эффектами — неоднородностью поля на краях электродов, в связи с чем обобщенные соотношения к расчету таких конфигураций поля отсутствуют. Таким образом, для расчета случая несимметричной конфигурации электродов, при котором основную роль будет играть именно неоднородное электрическое поле, необходима разработка нового алгоритма к расчету таких полей, а также «краевых» эффектов поля конденсатора любой конфигурации.
Соотношение к расчету напряженности стационарного электрического поля, исходя из определения данной величины, может быть записано для двумерного случая как вектор в виде набора координат [4, с. 2]:
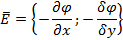
Принимая во внимание, что в расчетной области между пластинами конденсатора отсутствуют свободные заряды, для вычислений потенциала используем уравнение Лапласа, которое для двумерного случая может быть записано в виде [4, с. 8]:
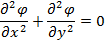
Данное уравнение дополним краевыми условиями нескольких видов исходя из особенностей расчетной области, которая представлена на рисунке 3.

Рис. 3. Расчетная область плоского несимметричного конденсатора.
Для границ расчетной области, которые должны находиться на достаточном удалении от пластин конденсатора, примем потенциал равным нулю, то есть:
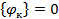
Для верхней и нижней пластин конденсатора потенциал должен быть различен, известен и задан условиями расчета, то есть:
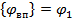
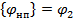
Для численного расчета приведенные выше соотношения аппроксимируются с использованием конечно-разностного метода. Таким образом, для получения результата, необходимо построить численный алгоритм к вычислению потенциала в точках между и вокруг пластин конденсатора, учитывающий постоянные значения потенциала как на границе, так и внутри расчетной области.
Блок-схема разработанного алгоритма представлена на Рисунке 4. Вследствие того, что рассматривается статическое электрическое поле, можно, без больших потерь в производительности, вместо итерационного способа расчета использовать единовременное построение и решение системы уравнений для всех точек потенциала. Однако, для расчета потенциала в рамках рассматриваемой задачи, с учетом наличия «внутренних» краевых условий, указанный способ нуждается в модификации.
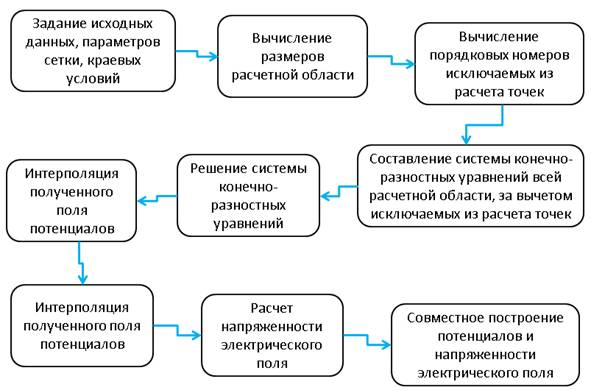
Рис. 4. Блок-схема алгоритма к расчету напряженности поля несимметричного конденсатора
Внутренние краевые условия требуют, чтобы, при использовании способа «единовременного» расчета, из вычислений были исключены те уравнения, которые описывают потенциал точек конденсатора, так как он задается заранее и поддерживается постоянным в течение всего срока эксплуатации установки. Для этой цели предлагается вычислять координаты точек конденсатора на расчетной сетке, а также их порядковые номера, и затем исключать из системы алгебраических уравнений, описывающих потенциал по всей расчетной области, уравнения для расчета уже известных значений потенциала пластин конденсатора. Таким образом исключаются ошибки, связанные с возможностью повторного расчета и замены значений потенциала, повышается точность значений, так как используются максимально достоверные данные из соседних точек расчетной сетки.
Приведенный алгоритм расчета был апробирован на двумерном расчете плоского несимметричного конденсатора с параметрами, представленными в Таблице 1.
Таблица 1
Исходные данные для апробации алгоритма.
|
Параметр, единица измерения: |
Значение: |
|
Длина верхней пластины конденсатора, м |
0,5 |
|
Длина нижней пластины конденсатора, м |
0,1 |
|
Напряжение на верхней пластине конденсатора, В |
2000 |
|
Напряжение на нижней пластине конденсатора, В |
0 |
|
Расстояние между пластинами конденсатора, м |
0,2 |
|
Количество точек расчетной сетки в горизонтальном направлении, штук |
100 |
|
Количество точек расчетной сетки в вертикальном направлении, штук |
200 |
Результаты апробации приведены на рисунке 5, где показаны результаты совместного расчета полей потенциала и напряженности электрического поля в исследуемой области.
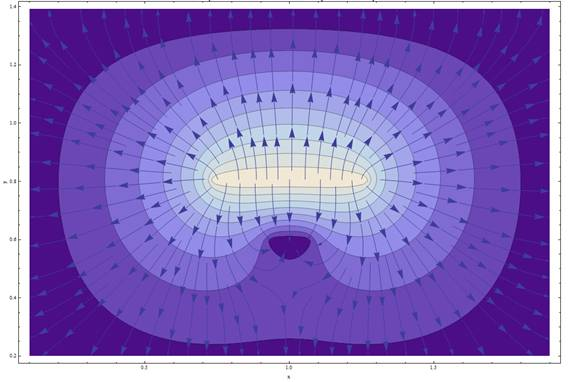
Рис. 5. Иллюстрация совмещенных скалярного поля потенциала (белое — 1800–2000 В, темное — 0–200 В) и векторного поля напряженности в расчетной области
Видно, что поля не смещены относительно друг друга и физическая природа передана верно — вектора поля напряженности направлены перпендикулярно эквипотенциальным поверхностям. Также наблюдается 4 зоны скопления силовых линий напряженности поля: у левого и правого краев верхней пластины, и у левого и правого краев нижней пластины.
В результате выполнения исследования был составлен и апробирован алгоритм к расчету неоднородного электрического поля плоского несимметричного конденсатора. Указанный алгоритм без существенных изменений может быть расширен для трехмерного случая, а также для конденсаторов и электродов более сложной конфигурации.
Дальнейшим направлением исследования является расчет поля сил диэлектрофореза, а также моделированием движения капли воды в поле сил, совместно с постановкой физического эксперимента по оценке степени достоверности результатов математического моделирования, а также предложение конкретных технических решений по модернизации принципа работы существующих электрообессоливающих установок.
Литература:
1. Байков Н. М., Колесников Б. В., Челпанов П. И. Сбор, транспорт и подготовка нефти. — М., «Недра», 1975. — 317 с.
2. Левченко Д. Н. Эмульсии нефти с водой и методы их разрушения / Д. Н. Левченко, Н. В. Бергштейн, А. Д. Худякова, Н. М. Николаева. — М., Издательство «Химия», 1967. — 200 с.
3. Панченков, Г. М. Поведение эмульсии во внешнем электрическом поле / Г. М. Панченков, Л. К. Цабек. — М.: Химия, 1969. — 190 с.
4. James R. Nagel Solving the Generalized Poisson Equation Using the Finite-Difference Method (FMD). URL: http://www.ieeeaps.org/pdfs/ FA_Numerical_Poisson_Nagel.pdf (дата обращения: 28.08.2014).







