Введение
Микрополярная (моментная) модель [1], предназначенная для описания напряженно-деформированного состояния композитов, гранулированных, порошкообразных сред, является основной моделью механики сплошных сред, учитывающей микроструктуру материала. Особую актуальность математические модели материалов со структурой получили в последнее время в связи с развитием микро- и нанотехнологий. В модели микрополярной среды кроме поступательного движения, которое характеризуется перемещением u, рассматриваются независимые повороты частиц 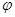 , а наряду с тензором напряжений с компонентами
, а наряду с тензором напряжений с компонентами 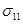 ,
, 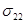 ,
, 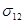 ,
, 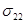 , вводится несимметричный тензор моментных напряжений с компонентами
, вводится несимметричный тензор моментных напряжений с компонентами 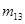 ,
, 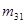 .
.
Вопросы численной реализации моментной модели в изотропном случае рассматриваются в [2–4]. В настоящей работе приводится вычислительный алгоритм для численного моделирования микрополярных ортотропных упругих стержней.
Математическая модель
Уравнения плоской динамической задачи, описывающие поведение ортотропного упругого стержня высотой 2h и длиной a, имеют вид [5, 6]:
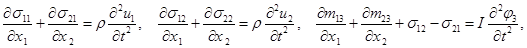
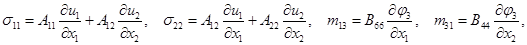
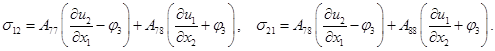 (1)
(1)
Здесь ρ – плотность среды; I – мера инерции среды при вращении; A11, A12, A22, A77, A78, A88, B66, B44 – феноменологические параметры упругости для ортотропной среды.
На основе гипотез, предложенных в работе [5], в предположении малости высоты стержня по сравнению с его длиной (2h<<a) и представлении перемещений и поворота в виде
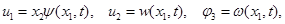
с учетом обозначений
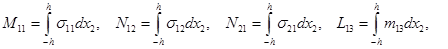
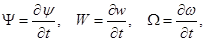
система уравнений (1) динамического изгиба микрополярных ортотропных упругих стержней с независимыми полями перемещений и вращений приводится к виду:
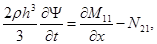
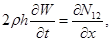
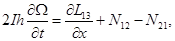
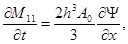
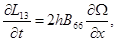 (2)
(2)
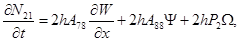
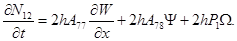
Здесь 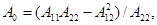
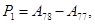
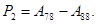
Систему уравнений (2) можно записать в матричной форме
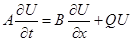 (3)
(3)
относительно вектор-функции U, включающей в себя компоненты линейной и угловых скоростей частиц, а также компоненты тензоров напряжений:
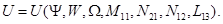
Матрицы-коэффициенты системы A и B симметричны, матрица Q антисимметрична:
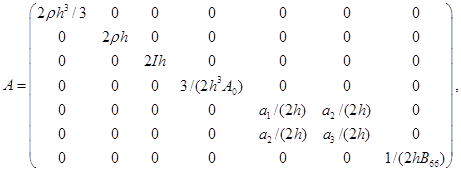
где 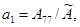
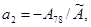
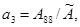
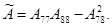 Ненулевые компоненты матриц
Ненулевые компоненты матриц 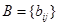 и
и 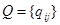 :
:
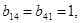
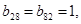
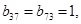
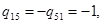
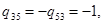
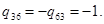
При выполнении неравенств, гарантирующих неотрицательность упругой энергии:
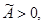
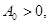
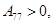
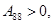
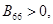
матрица A положительно определена, и система уравнений (3) является гиперболической по Фридрихсу. Для такой системы выполняется закон сохранения энергии
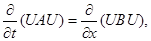
из которого следует корректность постановки задачи Коши и краевых задач с диссипативными граничными условиями. Характеристические свойства системы описываются уравнением
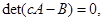
корни которого, скорости волн, равны:
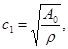
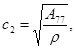
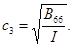
Полную систему левых собственных векторов образуют 6 векторов, соответствующих ненулевым собственным числам: 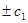 ,
, 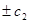 ,
, 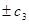 , и один вектор для
, и один вектор для 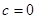 .
.
Начальные данные краевой задачи предполагают задание вектор-функции U при 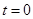 . Граничные условия могут быть сформулированы в терминах скоростей или напряжений:
. Граничные условия могут быть сформулированы в терминах скоростей или напряжений:
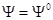 или
или 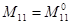 ,
, 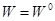 или
или 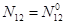 ,
, 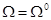 или
или 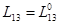 .
.
Вычислительный алгоритм
Алгоритм численного решения задачи основан на методе двуциклического расщепления по пространственным переменным и времени. Для системы уравнений общего вида (3) процедура расщепления состоит из трех этапов. На первом этапе решается одномерная задача в направлении x на интервале 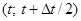 . На четвертом этапе к системе линейных обыкновенных дифференциальных уравнений применяется схема Кранка-Николсон второго порядка точности с полным шагом по времени. Третий этап – повторный пересчет задачи в направлении x на интервале
. На четвертом этапе к системе линейных обыкновенных дифференциальных уравнений применяется схема Кранка-Николсон второго порядка точности с полным шагом по времени. Третий этап – повторный пересчет задачи в направлении x на интервале 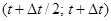 .
.
Процедура расщепления приводит к одномерным системам:
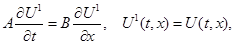 (4)
(4)
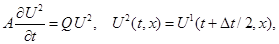 (5)
(5)
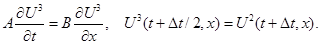 (6)
(6)
Искомое значение 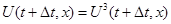 . Рассматриваемый метод двуциклического расщепления имеет второй порядок точности по пространственным переменным и времени, если на его этапах используются схемы второго порядка, и обеспечивает устойчивость численного решения при выполнении условия устойчивости Куранта-Фридрихса-Леви.
. Рассматриваемый метод двуциклического расщепления имеет второй порядок точности по пространственным переменным и времени, если на его этапах используются схемы второго порядка, и обеспечивает устойчивость численного решения при выполнении условия устойчивости Куранта-Фридрихса-Леви.
К каждой из одномерных задач (4), (6) применяется явная монотонная разностная схема Годунова типа "предиктор-корректор", устойчивая при выполнении условия Куранта-Фридрихса-Леви. На втором этапе метода расщепления в (5) к системе обыкновенных дифференциальных уравнений применяется неявная разностная схема Кранка-Николсон [7]:
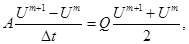
где m – номер шага по времени.
Численное решение представлено на рис. 1. На левой границе стержня действует Λ-образный импульс моментного напряжения L13, начальные данные нулевые. Длительность импульса – 10 шагов по времени, размер сетки – 1000 ячеек, пройдено 1000 шагов по времени. Физические параметры для расчетов были выбраны согласно [5]: ρ = 1114 кг / м3, I = 5.31e-6 кг / м,A0 = 5.2e6 Па,A77 = 4.6e6 Па, A88 = 4.8e6 Па, A78 = 0.4e6 Па, B66 = 300 Н. Длина стержня a варьировалась: a = 0.1 м (рис. 1, слева), a = 0.2 м (рис. 1, справа), h = a / 40. Результаты расчетов показывают, что при фиксированном времени угловая скорость и моментное напряжение представляют собой осциллирующие функции.
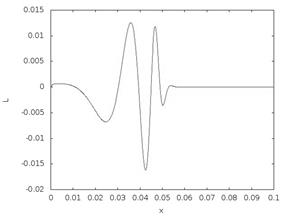
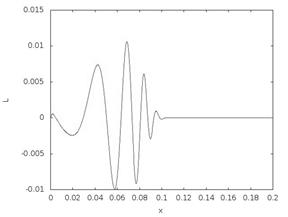
Рис. 1. Линии уровня моментного напряжения L13: a = 0.1 м (слева), a = 0.2 м (справа)
Для верификации работы численного алгоритма использовалось аналитическое решение задачи о распространении монохроматической волны в стержне, полученное в работах [5, 6].
Заключение
Динамическая модель микрополярных ортотропных упругих стержней с независимыми полями перемещений и вращений приведена к симметричной гиперболической по Фридрихсу форме, позволяющей эффективно применять вычислительные алгоритмы. Для численного решения разработан вычислительный алгоритм, основанный на методе двуциклического расщепления с применением схемы Годунова и Кранка-Николсон. Выполнены численные расчеты полей скоростей и напряжений в задаче о действии импульсной Λ-образной нагрузки.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (код проекта 14-01-00130).
Литература:
1. Cosserat E., Cosserat F. Theorie de Corps Deformables // Chwolson's Traite Physique. 2nd ed. – Paris, 1909. – P. 953–1173.
2. Варыгина М.П., Садовская О.В. Параллельный вычислительный алгоритм для решения динамических задач моментной теории упругости // Вестник Красноярского госуниверситета, 2005. – Вып. 4. – С. 211–215.
3. Варыгина М.П., Киреев И.В., Садовская О.В., Садовский В.М. Программное обеспечение для анализа волновых движений в моментных средах на многопроцессорных вычислительных системах // Вестник Сибирского государственного аэрокосмического университета им. акад. М.Ф. Решетнева, 2009. – Вып. 2 (23). – С. 104–108.
4. Sadovskii V., Sadovaskaya O. and Varygina M. Numerical solution of dynamic problems in couple-stressed continuum on multiprocessor computer systems // International Journal of Numerical Analysis and Modeling, Series B, 2011. – V. 2, No. 2-3. – P. 215–230.
5. Маргарян Л.М., Саркисян С.О. Математическое моделирование динамики микрополярных анизотропных (ортотропных) упругих тонких балок // Известия Национальных наук Армении, 2012. – Т. 65, №1. – С. 17–28.
6. Маргарян Л.М. Построение прикладных моделей динамических состояний микрополярных упругих ортотропных стержней и их сравнительный анализ // Автореферат дисс. канд. физ.-мат. н., Ереван, 2012. – 36 с.
7. Марчук Г.И. Методы вычислительной математики. – М.: Наука, 1989. – 608 с.







