Электроимпульсные технологии очистки поверхностей от налипания различных веществ находят широкое применение в строительстве, машиностроении, железнодорожном транспорте, теплоэнергетике и других сферах производственной деятельности. Это связано с необходимостью удаления со стенок и конструктивных элементов оборудования различных материалов (например, сыпучих материалов, накипи и прочных отложений с внутренних поверхностей различного технологического оборудования, снега и наледи с карнизов и кровель домов). За последнее десятилетие предложено большое многообразие схемных и конструктивных решений устройств электроимпульсной технологии очистки поверхностей от промышленных загрязнений, нашедших отражение в научных работах и патентах, опубликованных и зарегестрированных в России и за рубежом [1, 2].
Принцип действия электроимпульсной очистки загрязненных поверхностей (рис. 1) основан на использовании энергии ударной волны в объекте воздействия, образующейся в результате взаимодействия индуцированных в нем вихревых токов с мощным импульсом магнитного поля, созданным электрическим разрядом емкостного накопителя на катушку индуктора. При продолжительности прохождения импульса тока по катушке индуктора в пределах 0,2 — 1 мс в объекте воздействия выделяется достаточная мощность и генеририруется ударная волна, обеспечивющая очистку поверхности от налипших материалов [3].
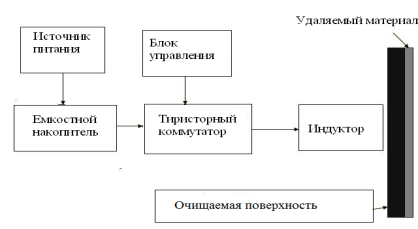
Рис. 1. Структурная схема электроимпульсной установки
Электромагнитные процессы преобразования энергии импульсного электрического разряда, происходящие в цепи катушки индуктора и в магнитном поле, индуцирующем вихревые токи в электропроводном объекте, сложным образом связаны между собой и определяют особенности характера протекающего переходного процесса, как в цепи катушки индуктора, так и магнитном поле объекта воздействия.
В данной статье предлагается цепно-полевой подход к решению задачи переходных процессов при электромагнитных взаимодействиях магнитного поля индуктора с индуцированными токами в токопроводной поверхности с использованием комплекса программ Elcut 6.0 (профессиональная версия).
В качестве базовой конструкции индуктора электроимпульсной установки (рис. 2) используется однослойная дисковая катушка с внешним диаметром D, намотанная в виде спирали медной шиной на узкое ребро и круглый изоляционный цилиндр диаметром d. Электропроводная поверхность представляет собой алюминиевый диск диаметром D и толщиной h, расположенный в непосредственной близости к торцевой поверхности индуктора на расстоянии δ, который полностью закрывает собой витки. К дисковой катушке в соответствии со структурной схемой рис 1 через тиристорный коммутатор подключается предварительно заряженный до напряжения U источника питания емкостной накопитель (конденсатор) емкостью C.
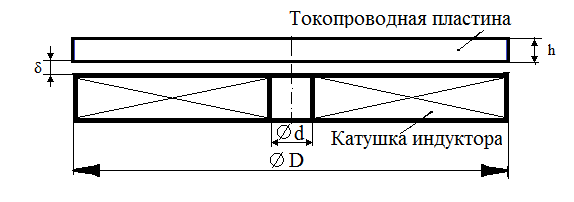
Рис. 2. Система: катушка индуктора — токопроводная пластина
Решение задачи расчета магнитного нестационарного поля электроимпульсной установки позволяет оценить эффективность электромагнтных взаимодействий и состоит из следующих стадий:
- Задание исходных данных для расчёта магнитного нестационарного поля, в качестве которых используются основные геометрические размеры индуктора и число витков катушки, толщина алюминиевого диска, расстояние между диском и поверхностью катушки индуктора, ёмкость конденсатора, начальное значение напряжения на конденсаторе в момент коммутации.
- Принятие допущения об осесимметричном характере нестационарного магнитного поля катушки индуктора, вследствие осевой симметрии базовой геометрии магнитной системы индуктора — токопроводящая поверхность, а также математическая постановка решения задачи расчета нестационарного магнитного поля.
Математическая формулировка осесимметричной задачи расчета поля сводится к преобразованию уравнений Максвелла и получению уравнения относительно векторного магнитного потенциала в цилиндрической системе координат
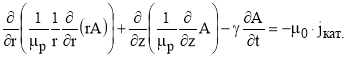 ,(1)
,(1)
где A = ![]() — векторный магнитный потенциал, имеющий также как вектор плотности тока
— векторный магнитный потенциал, имеющий также как вектор плотности тока ![]() одну составляющую, перпендикулярную плоскости zr расчетной модели; p — число линейных изотропных кусочно-однородных подобластей расчетной модели, на которые разбивается магнитное поле с постоянной относительной магнитной проницаемостью среды
одну составляющую, перпендикулярную плоскости zr расчетной модели; p — число линейных изотропных кусочно-однородных подобластей расчетной модели, на которые разбивается магнитное поле с постоянной относительной магнитной проницаемостью среды ![]() .
.
Плотность индуцированных вихревых токов в алюминиевом диске определяется из уравнения
![]() (2)
(2)
Электрическое состояние цепи при разряде предварительно заряженного конденсатора до напряжения источника питания на катушку индуктора описывается уравнением
![]() (3)
(3)
где![]() — полное потокосцепление катушки индуктора, изменяющееся во времени при переходном процессе;
— полное потокосцепление катушки индуктора, изменяющееся во времени при переходном процессе;![]() – активное сопротивление катушки.
– активное сопротивление катушки.
Объединение уравнений (1) — (3) в систему для совместного решения с учетом заданных граничных и начальных условий основывается на построении расчетной модели нестационарного магнитного поля в комплексе программ Elcut (рис. 3) с присоединенной электрической цепью (рис. 4).
При построении геометрии модели (рис. 3) принята единица длины — миллиметры. Внешние границы расчетной модели расположены таким образом, чтобы имитировать бесконечное удаление (отсутствие изменения поля в нормальном направлении к границе). Расчетная область ограничена прямоугольником размерами 50 мм ![]() 80 мм. На границе расчетной области принимается условие
80 мм. На границе расчетной области принимается условие ![]() . Выделенные метки объектов (воздух, катушка, токопроводная пластина) характеризуются следующими физическими свойствами: относительная магнитная проницаемость воздуха, меди и алюминия
. Выделенные метки объектов (воздух, катушка, токопроводная пластина) характеризуются следующими физическими свойствами: относительная магнитная проницаемость воздуха, меди и алюминия ![]() ; электропроводность медного провода катушки индуктора
; электропроводность медного провода катушки индуктора ![]() и алюминиевого диска
и алюминиевого диска![]() .
.
На рис. 4 заряд конденсатора емкостью 150 мкФ производится от импульсного источника напряжения. Продолжительность импульса напряжения заряда конденсатора до напряжения 1000 В составляет 0,5 мс.
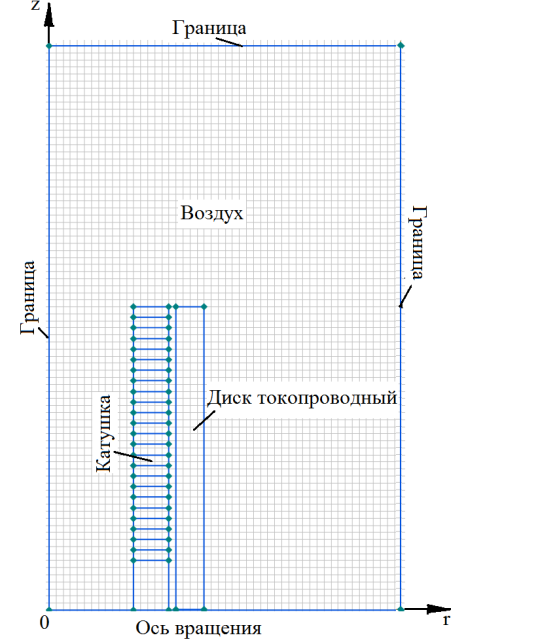
Рис. 3. Геометрия модели в окне пакета Elcut
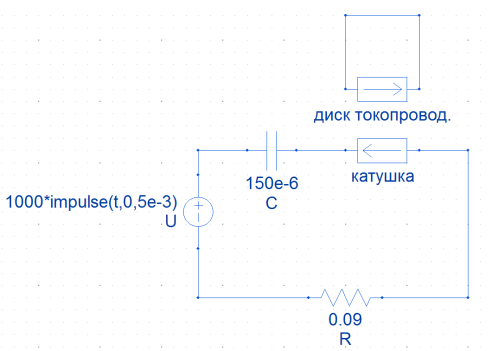
Рис. 4. Изображение электрической цепи в окне пакета Elcut
Для решения задачи нестационарного магнитного поля системы катушка индуктора — токопроводная поверхность область моделирования прокрывается сеткой из конечных треугольных элементов. При автоматическом шаге дискретизации расчетная область покрывается сеткой из конечных элементов, содержащей 9634 узлов. При временных параметрах моделирования интегрирования по времени с нуля до 5,5 мс с шагом 10 мкс время расчета переходного процесса составляет 38 минут. Решение задачи запоминается каждые 10 мкс, начиная с момента времени 4,9 мс.
Расчётная картина силовых линий магнитного поля системы катушка индуктора — токопроводная пластина в момент прохождения максимума тока через катушку индуктора при разряде конденсатора показана на рис. 5 А.
Направление обхода контура в области катушки (рис. 5 Б), занятой током, позволяет с помощью интегрального калькулятора пакета Elcut определить магнитодвижущую силу (МДС) катушки по закону полного тока и построить график временной зависимости ампервитков при переходном процессе.
Обход контура на рассчитанной картине магнитного поля в области токопроводной пластины (рис. 6 А) позволяет с помощью интегрального калькулятора пакета Elcut построить временную зависимость индуцированных вихревых токов при переходном процессе, представленную на рис. 6 Б.
По результатам решения задачи в пакете Elcut максимум силы (пондеромоторной силы) электромагнитного взаимодействия магнитного поля, созданного ампервитками катушки индуктора с вихревыми токами, индуцированными в токопроводной пластине, приходится на максимум тока в электрической цепи при переходном процессе и составляет 6100 Н.
Использованный для решения задачи нестационарного магнитного поля системы катушка индуктора — электропроводная пластина в пакете Elcut 6.0 (профессиональная версия) цепно-полевой подход позволяет определить основные параметры и временные характеристики исследуемого физического процесса, связанного с электроимпульсной технологией очистки поверхностей.
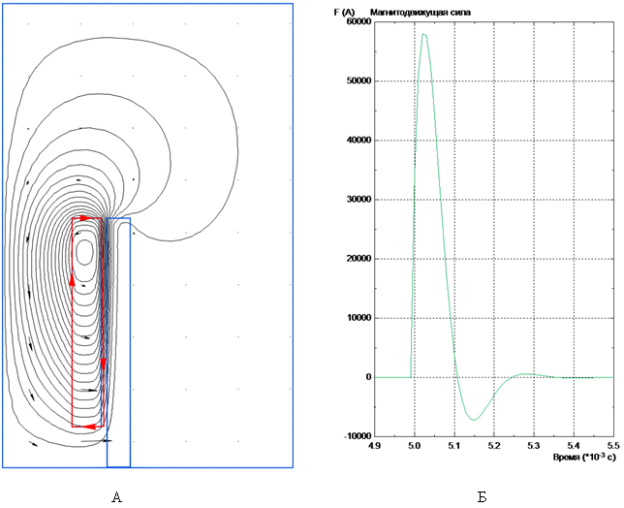
Рис. 5. А — Картина магнитного поля. Б — Изменение МДС катушки индуктора во времени
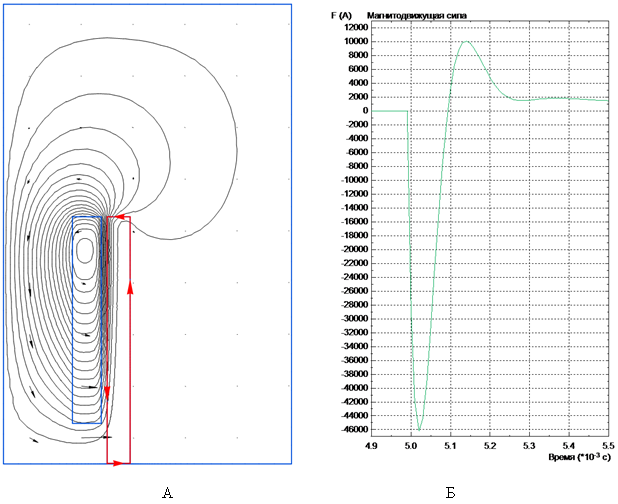
Рис. 6. Применение закона полного тока к определению мгновенных значений индуцированных вихревых токов в токопроводной пластине (а) и их временная зависимость при переходном процессе (б)
Литература:
- Патент № 2096269. Способ удаления отложений, преимущественно льда, с очищаемой поверхности обшивки и устройство его осуществления/ И.А. Левин — № 4671256/11 Заявл. 13.04.1989; Опубл. 20.11.1997.
- Patent № US5129598 A. Attachable electro-impulse de-icer/ Lowell J. Adams, Norbert A.Weisend , Jr., Thomas E. Wohlwender — Appl. No: 07/455,129; Filed: December 22, 1989.
- Шильников, П.Ю. Электроимпульсная очистка поверхностей / П.Ю. Шильников, В.А.Захаренко. — С. 254-255. Россия молодая. — 2013.







