При применении национальных педагогических технологий в учебном процессе и при использовании современных педагогических и информационно-коммуникационных технологий имеет важное значение создания электронных обучающих программ. Так как сегодня при применении современных педагогических технологий имеется достаточное учебно-методическое обеспечение (учебно-методические комплексы, тексты лекций), считающееся удобным источником для получения знаний учащимися. Однако с помощью этих источников учащемуся (студенту) неудобно проводить самоконтроль знаний, выявлять степень развития, а электронные обучающие программы создают для учащегося такие возможности.
Имеются различные варианты создания электронных обучающих программ. В нашей статье мы приведём технологию разработки изучаемой нами электронной обучающей программы.
Технология изготовления электронной обучающей программы основывается на дифференцированных и индивидуальных подходах, а также на линейных и разветвлённых программированных обучающих методах и на нижеследующих принципах:
1. Основываясь на дифференцированные подходы выбирается удобное для всех содержание изучаемого предмета, соответствующее образовательным целям.
2. Учебный предмет делится на модули.
Модуль – приведенный в удобный вариант при изучении теоретического содержания отрезок (часть, раздел) учебного предмета. “Модульное обучение” – комплекс приёмов, методов, процессов, средств и форм обучения (образования), исходящих из принципа «ускорения и повышения эффективности» образовательно-воспитательного процесса, то есть устанавливающий взаимосвязь между предметами, практичность содержания образования, связывающий цели обучения с ожидаемым результатом, гарантирующий достижение результатов, то есть один из методов (приёмов) национальной педагогической технологии.
В этой статье мы рассмотрев электронную обучающую программу на примере учебного предмета геометрии, осуществим метод модульного обучения при изучении тем предмета и доказательстве теорем с помощью информационно-коммуникационных технологий.
Приняв во внимание что предмет “Геометрия” есть один цельный предмет, приняв его как “макромодуль”, исходя из объёма и содержания данных в нём материалов, – разделим его на «большие», «средние» и «малые» модули. Затем выявим их цели и подцели и определим отведённое для них время.
3. Содержание изучаемого предмета основывается на образовательном методе линейного и разветвлённого программирования.
4. Содержание изучаемого предмета основывается на опорных выражениях и основных понятиях, и дифференцируется с помощью повторной структуризации. Усвоение дифференцированного учебного материала основывается на индивидуальном подходе.
5. Для студента создаётся возможность, исходя из метода линейного и разветвлённого программирования, самопроверки степени усвоения и повышения степени успеваемости.
6. Усвоение учащимся содержания учебного материала связывается с I,II,III,IV – алгоритмическими степенями усвоения и овладения опорных выражений и основных понятий.
7. Для каждой темы учебного материала или для каждого отдельного дифференцированного варианта модуля, составляется таксономия Б.Блума (дающая возможность I,II,III,IV-алгоритмических степеней усвоения) в соответствии с учебными целями: знать, понимать, применять, анализ, синтез, оценка, составляется тест или комплекс вопросов другой формы. При этом выражающие образовательные цели учебного содержания или цели учителя вопросы «Кого? Почему? Что? Когда и как?» превращаются в учебные цели учащегося и приводятся в форму контрольных вопросов, выражающих вопросы «Что знает и думает?», «Что делает?», «Что чувствует?».
8. При выявлении степени усвоения учащегося с помощью метода линейного программирования используется вариант учебного материала, удобный для всех, то есть основанный на дифференцированном подходе.
9. Улучшение степени усвоения учебного материала студентом осуществляется на основе метода разветвлённого программирования.
Для повышения степени усвоения учащегося применив дифференцированный вариант содержания учебного материала, учебный материал составляется повторно, на основе опорных выражений и основных понятий. Определяются контрольные задания, состоящие из тестовых вопросов и отдельный теоретический материал, удобный для создания возможности ещё более широкого и глубокого изучения материала, соответствующего каждому опорному выражению и основному понятию.
10. На основе приведённых принципов, учебный материал вводится в компьютер и для студентов (учащихся) создаётся возможность использовать его.
Обоснуем наши мысли о разработке электронной обучающей программы на примере темы «Треугольники» по предмету «Геометрия», изучаемому в академических лицеях.
Перед тем как дать определение понятию треугольник: задаются вопросы, тесты о понятии треугольника, об его сторонах, периметре, углах, высоте, видах треугольников, их свойствах, а также задачи по доказательству теорем и их решению. Учебный материал по теме «Треугольники», основываясь на программированный образовательный метод, разделим на малые части:
1-часть. Понятие треугольника, изучение его сторон, углов, периметра и диагоналей. Кроме того, изучение понятий и свойств, являющихся опорой при доказательстве теорем по теме «Треугольники».
2-часть. Свойства треугольников и теоремы, изучение их доказательств.
3-часть. Самостоятельный рост степени усвоения учащегося и изучение комплекса тестов для его развития.
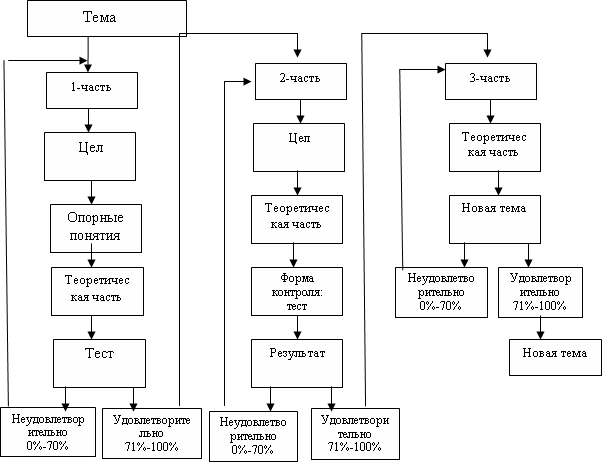
- Разветвлённый программированный образовательный проект приведёт в таблице.
Если степень усвоения учащегося в 1-части (проверяется на основе теста) считается такой, что даны правильные ответы на вопросы от 0% до 70 % вопросов, то разветвлённая обучающая программа не переводит его в изучение очередной 2-й части. Так как обучающая программа считает, что учащийся не усвоил эту тему и возвращает его к повторному изучению пройденной 1-части, имеющейся в компьютере, для исправления ошибок. Затем для того, чтобы выявить усвоение этого пройденного материала разветвлённая программа (на основе тестовых вопросов) проверяет знания. Если программа считает, что учащийся ответил на 71-100% вопросов, заданных по 1-части, то учащайся переводится на изучение “2-части”. В противном случае, для исправления ошибок, его возвращают в изучению понятий «Угол», «Точка», «Отрезок» и других, которые изучались раньше и связаны с темой «Треугольники» и усвоение им этого материала опять проверяется тестом. Таким образом, учащийся привлекается к самостоятельному изучению пройденного материала на основе системного подхода. При изучении учебного материала на основе разветвлённой программы, создаётся возможность для самостоятельной проверки учащимся своих знаний, а также для самостоятельной работы над собой.
Таблица
Проект дифференцированного программированного образования
|
1-часть |
|||||||
|
Тема |
Опорные понятия |
Теоретическая часть |
Контрольне вопросы |
Результат |
|||
|
ТЕМА: треугольники |
Треугольник, углы (концы) треугольника, стороны треугольника, внутренние углы треугольника, луч, лежит на одной полуплоскости, поверхностно совпадает. |
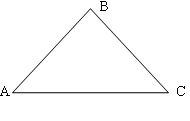
Фигура, состоящая из не лежащих на прямой линии трёх точек, и трёх отрезков, которые попарно соединяют эти точки называется треугольником.(Рис. 1.) Эти точки называются концами треугольника (На рис. 1.) точки А, В, С), а отрезки называются сторонами треугольника (АВ, АС, ВС). Углы, расположенные внутри треугольника называются внутрениими углами треугольника. Часть прямой линии, заданная из точки и состоящей из лежащих на одной стороне от неё точек называется полупрямой линией или лучом. |
1.Фигура состоящая из трёх точек, не лежащих на одной прямой линии и попарно соединяющая эти точки тремя отрезками называется ..................... . А) треугольник В) угол С) четырёхугольник D) отрезок 2. Фигура, состоящая из трёх точек, не лежащих на одной прямой линии и из трёх отрезков, соединяющих попарно эти точки называется треугольником, эти точки называются ……….. треугольника, а отрезки называются ………….. А) треугольник В) концы, стороны С) стороны, концы D) отрезок 3. Углы внутри треугольника называются ................... треугольника, а соседние с ними углы называются ........................... А) концами В) концами, сторонами С)внутренними и внешними углами D)углами 4. Если соответствующие (подобные) углы и соответствующие (подобные) стороны одного треугольника равны, то такие треугольники называются ........... А) равными (подобными) В) равносторонними (равнобедренными) С) неравными D) правильными ……………………………. ……………………………. …………………………….
|
0%-60 %-неудовлетворительно, 70%-100% удовлетворительно(хорошо, отлично)
|
|||
|
|
2-часть |
||||||
|
|
Теорема. Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам и углу между ними второго треугольника , то такие треугольники равны. |
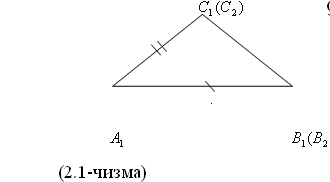
доказательство тЕОРЕМы. Пусть в треугольниках АВС и А1В1С1 А =А1, АВ=А1В1 АС=А1С1 (рис.2.). Докажем равенство треугольников, то есть, что у них В=В1, С=С1, ВС=В1С1. Согласно аксиоме о наличии равного (подобного) треугольника равного заданному треугольнику, имеется равный треугольнику АВС треугольник А1В2С2, его конец В2 расположен на луче А1В1, а конец С2 лежит (расположен) относительно прямой линии А1В1 вместе с концом С1 на одной полуплоскости. Так как А1В1=А1В2, то согласно аксиоме о постановке отрезков точка В2 располагается поверх точки В1. Так как В1А1С1=В2А1С2, то согласно аксиоме о постановке углов, луч А1С2 располагается поверх луча А1С1. Точно также, так как А1С1=А1С2, то конец С2 располагается поверх конца С2. Таким образом треугольник А1В1С1 располагается поверх треугольника треугольника А1В2С2, и значит, равен треугольнику АВС.
|
1. Отрезок АВ пересекается с отрезком CD в точке О, эта точка О является центром любого отрезка. Если АС=10 см, то найдите длину отрезка BD. А) 20 см В) 5 см С) 15 см D) 10 см 2. Если …….сторона(стороны) одного треугольника и угол между ними соответственно равны …..стороне (сторонам) и углу между ними, то такие треугольники будут равны (подобны). А) две стороны В) одна сторона С) три стороны D) нет верного ответа 3. Если треугольники равны, то ……. этих треугольников тоже будут равны. А) две стороны и углы между ними В) три стороны С) одна сторона и прилегающие к ней углы D) все ответы верны. 4. Отрезок АВ пересекается с отрезком CD в точке О, эта точка О является центром каждого отрезка. Если АС=15 см, то найдите длину отрезка BD. А) 30 см В) 5 см С) 15 см D) 10 см ………………………. ……………………….. ……………………….
|
0%-60 %-неудовлетворительно, 70%-100% удовлетворительно(хорошо, отлично) |
|||
|
|
3-часть |
|
|||||
|
|
1. Пусть в треугольниках АВС ва А1В1С1 дано А=А1, АВ=А1В1, АС=А1С1, тогда какое равенство будет уместно?
2. Если две стороны одного треугольника равны 12 см а угол между ними равен 600 , то найдине соответствующие стороны и угол треугольника, подобного (равного) заданному треугольнику.
3. Если две стороны заданного треугольника соответственно равны, а угол одного из них равен 600 , то выясните соответствующий угол у второго треугольника.
4.Если две стороны треугольника равны, а сумма прилегающих к ней углов равна 1500, то найдите угол на конце подобного ему треугольника.
5. Найдите ряд, где приведена правильная теорема. А) Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники называются подобными (равными). В) Если соответствующие углы и соответствующие стороны треугольников равны, то такие треугольники называются подобными (равными). С) На любой полупрямой линии с её начальной точки можно поставить единственный (то есть только один) отрезок заданной длины. D) Все приведённые ответы верны. 6. Если две стороны треугольника равны, а сумма прилегающих к ней углов равна 1200, определите угол на конце подобного (равного) ему треугольника.
|
0%-60 %-неудовлетворительно, 70%-100% удовлетворительно(хорошо, отлично) |
|
||||
Разработка электронных обучающих программ на основе разветвлённой программы: выбор образовательного содержания каждого учебного предмета, его переструктуризация исходя из опорных выражений и основных понятий; разработка контрольных вопросов, основанных на системную обратную связь, для каждой части учебного материала по теме занятия; эти вопросы помогут учащемуся осознать свои ошибки, исправить их; целесообразно вначале самостоятельное повторение пройденного учебного материала. Эта работа выполняет важную задачу, требующую большого труда, времени, знаний, умений и навыков, а также возможностей.
Рис.1. Схема работы электронного учебника, созданного на основе разветвлённой программы
Если подобные вышеописанным, уроки станут проектироваться с использованием информационно-коммуникационных технологий, то эффективность образования (обучения) резко возрастет.