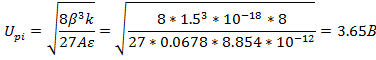Основная функция мехатронных систем состоит в целенаправленном перемещении тела, обладающего массой. Основой для этого, в большинстве случаев, служит двустороннее преобразование энергии из механической в электрическую, и наоборот. Двустороннее преобразование энергии создает ключевое условие для главной цели системы – целенаправленного перемещения. Имеющиеся сегодня в распоряжении разнообразные физические принципы преобразования энергий, например, электростатика, пьезоэффект или электромагнетизм, позволяют создать их функциональную конструктивно компактную интеграцию в одном устройстве – преобразователе. При этом электромеханические преобразователи применяются в мехатронике не только в качестве приводов, но и в качестве датчиков. В представленной статье рассматриваются некоторые вопросы, связанные с созданием и исследованием компьютерных моделей мехатронных преобразователей на основе использования языка Modelica.
1.Свойства мехатронных преобразователей. Создание моделей преобразователей, являющихся ядром мехатронной системы, является актуальной проблемой при конструировании мехатронных модулей и систем. Наличие компактных, точных, удобных в использовании моделей позволит сократить затраты на проектирование и разработку мехатронных устройств, а также позволит оценить пригодность системы для практического использования без создания опытных образцов.
Построение модели мехатронного преобразователя подразумевает объединение частей, относящихся к различным физическим областям. При этом модель должна работать в обоих направлениях, выполняя функции датчика и привода. Конечной целью моделирования является построение унифицированных наглядных абстрактных моделей. Поэтому, для удобного отображения процессов, происходящих в элементарном мехатронном преобразователе (далее - ЭМП), в качестве базовой структуры выбрана четырехполюсная модель, содержащая два механических фланца и два электрических контакта (рисунок 1). Сам ЭМП, при этом, представляет собой блок, в котором происходят преобразования энергии из механической в электрическую, и наоборот [1].
Рис.1. Четырехполюсная структура модели элементарного мехатронного преобразователя
При работе преобразователя
в режиме привода, на него подается электрический сигнал,
характеризуемый током
и напряжением
.
Электрический сигнал преобразовывается в ЭМП в механическую силу
,
вызывающую перемещение подвижного элемента преобразователя
.
При работе преобразователя в режиме датчика, на вход подается внешнее воздействие в виде силы или перемещения, которое вызывает изменение электрических характеристик преобразователя.
При разработке унифицированных моделей мехатронных преобразователей серьезные трудности представляют разнородность процессов, происходящих в разных видах преобразователей, большое разнообразие конструкций, и отсутствие единого математического описания. Также проблемой при моделировании является мультидоменный характер преобразователей, то есть, необходимость объединения в одной модели элементов из разных физических областей.
Главными требованиями к моделям являются возможность реализации на базе одной модели как функций датчика, так и привода, а также возможность многократного использования моделей при проектировании мехатронных устройств. Эти условия предъявляют нетривиальные требования к средствам и методам моделирования.
2.Сравнение существующих средств моделирования. В современных инструментах компонентного моделирования систем можно выделить два основных направления:
направление «блочного» моделирования;
направление «физического» моделирования.
Инструменты так называемого «блочного моделирования» ориентированы на графический язык иерархических блок схем. Элементарные блоки являются либо предопределенными, либо могут конструироваться с помощью некоторого специального вспомогательного языка более низкого уровня, как правило, Си или Fortran, не поддерживающего объектно-ориентированное программирование. Собранную схему можно объявить типовым блоком следующего уровня или подсистемой [2]. Модель можно собрать из имеющихся блоков с использованием направленных связей и параметрической настройки. Для некоторых специальных наборов блоков возможно использование и ненаправленных связей [2, 3].
Этот подход является несколько устаревшим, однако он доминирует в настоящее время. Наиболее известными современными представителями этого направления являются: подсистема SIMULINK пакета MATLAB (MathWorks, Inc.), EASY5 (MSC Software); VisSim (Visual Solution); МВТУ (МГТУ им. Н.Э.Баумана) [2].
Этот подход не может быть использован для компонентного моделирования мехатронной системы, так как:
имеет направленные связи (модель может выполнять функции только датчика или только привода);
поддержка мультидоменного компонентного моделирования с ненаправленными связями только для некоторых специальных наборов блоков;
нет возможности описания новых компонентов средствами входного языка;
несоответствие структуры моделируемого объекта и структуры модели;
нет поддержки объектно-ориентированного описания моделей.
Направление «физического» моделирования представлено пакетами, поддерживающими новый унифицированный язык моделирования физических систем Modelica. Modelica - это объектно-ориентированный язык моделирования, основанный на математическом описании моделей сложных природных или искусственных систем, и предназначенный для компьютерной симуляции динамических процессов [5, 6]. Этот язык специально создан для моделирования физических систем. Он обеспечивает возможность эффективного расширения библиотек и облегчения повторного использования знаний, приобретенных при создании предыдущих моделей. Язык Modelica уже хорошо зарекомендовал себя в самых разных областях промышленности. Toyota, BMW, Ford и многие другие крупные производители используют его в своих проектных подразделениях для создания моделей двигателей, трансмиссий и электронных систем управления.
При этом язык является свободно распространяемым, и на его основе созданы уже немало инструментальных средств промышленного уровня качества, среди которых также есть свободно распространяемые. Например, OpenModelica или SimulationX Student Edition. Ограничения студенческой версии SimulationX касаются только собственных программных блоков, тогда как библиотеки Modelica остаются полностью свободно используемыми и редактируемыми. При этом главным плюсом среды является наличие удобного визуального дизайнера новых Modelica-блоков.
3. Язык Modelica.
Рассмотрим основные свойства «физического» объектно-ориентированного моделирования на примере языка Modelica, определяющие пригодность данного принципа для создания моделей мехатронных преобразователей [7,8].
Данный язык основывается на уравнениях, взамен операций присваивания. Моделирование на базе уравнений расширяет возможности повторного использования уже созданных объектов, так как уравнения не определяют направление потока данных. Например, в любом императивном языке запись “x=y*z”, означает: вычислить произведение y и z, а затем присвоить полученное значение ячейке памяти с адресом х. В Modelica же это означает то же самое что в математике, то есть знак “=” – это не знак присваивания, а именно знак равенства. То есть, записав в Modelica “x=z*y;”, мы записали именно уравнение. В этом кроется незаметное на первый взгляд преимущество: записав одно уравнение, мы описываем сразу три варианта его использования. Неважно, какие две из трех переменных будут известны, программа всегда вычислит значение третьей. Тогда как, при описании этого уравнения на основе языка программирования с машинной семантикой оператора присваивания, для полного описания модели, характеризующейся данным уравнением, нам необходимо описывать все три возможные формы данного равенства, что многократно увеличивает трудоемкость при создании больших систем.
Modelica – представитель класса декларативных языков. Принципиальное отличие декларативного языка – описание не способа решения задачи, а самой задачи. То есть, мы записываем в программе не алгоритм решения задачи, а только ее описание. В основе языка Modelica лежит концепция соединяемых блоков. При соединении в соответствии с требуемой схемой автоматически генерируются соответствующие уравнения. Это делает язык простым для понимания и использования специалистами самых различных профилей и квалификаций.
Язык имеет возможность мультидоменного моделирования, то есть компоненты модели могут относиться к различным областям, таким как электротехника, механика, термодинамика и т.д., и эти компоненты могут связываться между собой. Также существует возможность объединения компонентов разной природы в одном блоке, для создания моделей преобразователей одного типа энергии в другой. Например, электромеханических или термогидравлических.
Modelica имеет большой набор встроенных библиотек, с возможностью их свободного расширения. Пользователь также может создавать свои собственные компоненты, используя при этом внутренний язык описания блоков. При этом могут использоваться встроенные типы или также созданные пользователем. Благодаря объектно-ориентированному подходу модели, созданные на языке Modelica, легко модернизируются. Это позволяет создавать на их основе более сложные модели.
Исходя из цели моделирования, состоящей в создании унифицированных наглядных абстрактных моделей мехатронных преобразователей двустороннего действия, принцип физического моделирования на языке Modelica имеет все необходимые свойства для придания моделям требуемых качеств.
4.Модели преобразователей. После разработки концепции создания мультидоменных моделей преобразователей с помощью языка Modelica автором была реализована библиотека моделей мехатронных преобразователей четырех типов: электростатических, пьезоэлектрических, электромагнитных и электродинамических. Для проверки соответствия свойств созданных моделей заявленным требованиям и сравнения результатов моделирования с реальными системами были созданы модели систем, включающих в себя мехатронные преобразователи.
5.Электростатический преобразователь. Для демонстрации результатов возьмем пример электростатического преобразователя, являющегося стандартным компонентом мехатронных систем, где он используется для выработки усилий и измерения величин движения. По причине очень малых вырабатываемых перемещений и сил, электростатические преобразователи нашли применение только в микроустройствах. Примерами применения ЭСП являются привод читающей головки CD-привода и электростатический акселерометр. Создание моделей данных преобразователей является очень актуальной задачей, так как создание опытных образцов микропреобразователей требует больших затрат, а практика показывает, что применение компьютерных моделей позволяет получить результаты очень близкие к реальным [9].
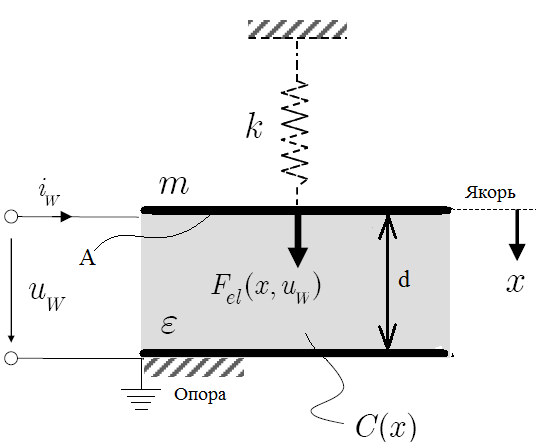
Конструктивно ЭСП, в общем случае, представляет собой конденсатор с перемещающимися относительно друг друга обкладками (рисунок 2). Изменение межэлектродного расстояния определяет трансформацию электрической энергии в механическую, и наоборот [1]. Возникающие между зарядами силы передаются через электроды на механическую систему. Емкость преобразователя, как и направление, и величина электростатической силы зависят от конструкции и используемых материалов.
Рис. 2. Электростатический преобразователь [1]
– электростатическая
сила; d - межэлектродное расстояние; ε –
диэлектрическая проницаемость диэлектрика; х – перемещение
электрода; С(х) – емкость преобразователя;
и
- ток и напряжение преобразователя соответственно; m
– масса подвижного электрода; A
– площадь поверхности электрода; k
– жесткость эластичной связи.
По причине того, что электростатическая сила всегда направлена так, чтобы увеличить емкость (на притяжение), то подвижный электрод должен иметь эластичную связь с механической структурой (рисунок 2).
Для данного преобразователя характерна следующая особенность. Для того чтобы, при отсутствии внешних воздействий, преобразователь находился в стабильном рабочем положении, сила растянутой пружины, связывающей подвижный электрод, должна равняться силе, вырабатываемой преобразователем. Это возможно при значениях управляющего напряжения меньше критического и при перемещении якоря меньше, чем на треть от общего межэлектродного расстояния. При нарушении этих условий подвижный электрод преобразователя неудержимо устремляется к неподвижному. Это явление получило название эффекта втягивания электрода (в англоязычной литературе Pull-in-phenomenon).
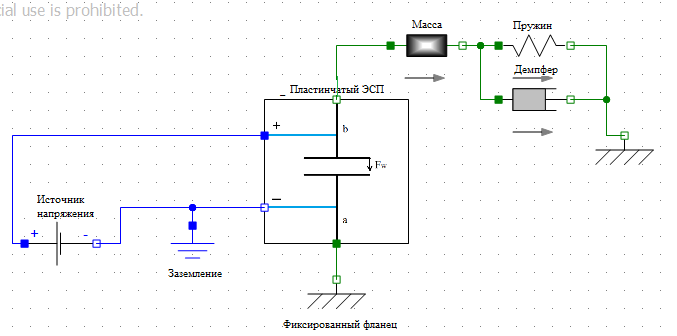
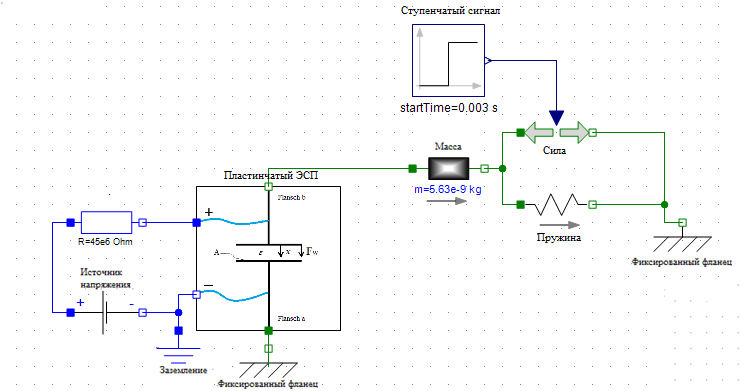
6. Проверка свойств модели. Для проверки явления втягивания электрода, была создана модель системы, состоящая из модели пластинчатого электростатического преобразователя а также элементов базовых библиотек Modelica: источника напряжения, заземления, двух фиксированных фланцев, пружины и демпфера (Рисунок 3).
Рис.3. Модель для проверки эффекта втягивания электрода
В качестве параметров модели преобразователя были приняты параметры микроэлектромеханического преобразователя фирмы Analog Devices, выполненного по 6-микрометровой технологии из кремния, с интегрированной электроникой [9]:
;
=
8.854e-12 Ас/Вмk= 8Н/м.
m= 5.63e-9кг.
Коэффициент демпфирования c=10.
Теоретическое значение критического напряжения втягивания для данного вида преобразователя определятся по формуле [1]:
Для проверки значения критического напряжения втягивания, сначала в качестве параметра модели источника напряжения было установлено значение 3.65 Вольт, затем была проведена симуляция и сохранены полученные результаты. Затем было установлено значение напряжения 3.66 Вольт, и симуляция была повторена.
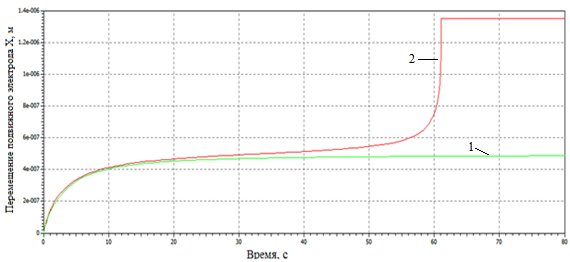
Рис.4. Перемещение подвижного электрода при разных напряжениях: 1 – напряжение 3,65В, 2 – 3,66В
Результаты показаны на рисунке 4. Первая линия соответствует напряжению питания 3,65 Вольт, а вторая - 3,66 Вольт. При напряжении питания 3,65 Вольт якорь занимает стабильное положение покоя, близкое к трети межэлектродного расстояния. При напряжении 3.66 Вольт градиент электростатической силы начинает преобладать над силой создаваемой пружиной, и подвижный электрод устремляется к неподвижному, то есть, возникает эффект втягивания электрода.
Результаты эксперимента подтвердили теоретическое значение критического напряжения втягивания и показали, что созданная модель функционирует корректно и пригодна для моделирования реальных преобразователей.
Для проверки возможности преобразователя выполнять функции датчика и демонстрации наличия постоянной связи между его электрической и механической частями была разработана модель для моделирования пассивного демпфирования колебаний. Термин «пассивное» демпфирование означает, что механическая часть модели не содержит каких-либо демпфирующих элементов. То есть движение происходит без потерь. Демпфирование колебаний при этом осуществляется за счет электромеханической связи, обеспечиваемой преобразователем. Механическая энергия рассеивается с помощью последовательного включения в электрическую цепь преобразователя резистора.
На рисунке 5 представлена модель для моделирования пассивного демпфирования колебаний. Ядром модели является модель электростатического преобразователя с параметрами из предыдущего примера. Модель также содержит новые элементы стандартных библиотек Modelica: резистор и сила, управляемая ступенчатым сигналом. Механическая часть модели не содержит демпфирующих элементов.
Рис.5. Модель для моделирования пассивного демпфирования колебаний
Оптимальное значение сопротивления определяется по формуле:
где
– частота собственного резонанса механической системы;
– емкость преобразователя при нулевом перемещении подвижного
электрода;
– отношение занятого положения равновесия при данном напряжении
и общего межэлектродного расстояния.
На
преобразователь подается напряжение
=3.4
В. При этом собственные колебания системы, создаваемые пружиной,
гасятся за счет потерь на резисторе и подвижный электрод занимает
положение покоя
при перемещении
,
то есть, его перемещение равно одной пятой от общего межэлектродного
расстояния.
Это значение является оптимальным для осуществления демпфирования
колебаний [1]. Затем, в момент времени t=0,0015с
на якорь начинает действовать внешняя сила равная
.
Система выходит из равновесия, а затем её колебания также гасятся за
счет активного сопротивления электрической части системы и подвижный
электрод занимает новое положение покоя. Результаты симуляции
показаны на рисунке 6.
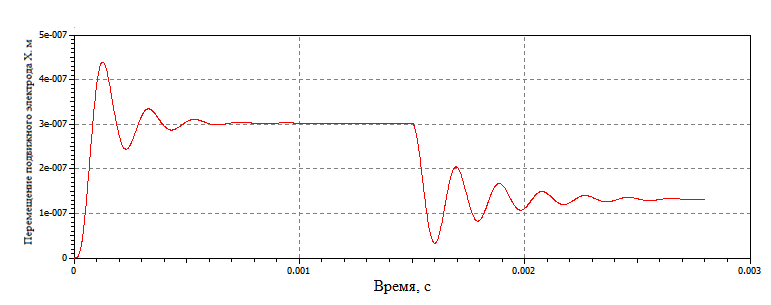Рис.6.
Перемещение
подвижного электрода при моделировании пассивного демпфирования
колебаний
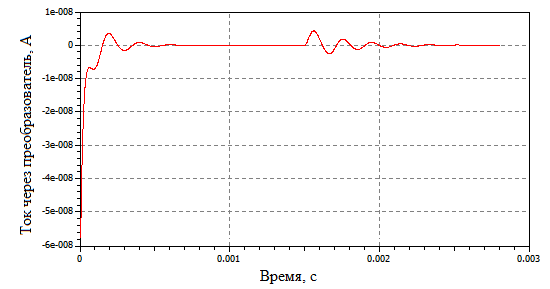
Также на этом примере можно показать возможность выполнения моделью функций датчика. На рисунке 7 показано изменение тока через преобразователь. Сравнив графики, представленные на рисунках 6 и 7, можно увидеть, что в ответ на перемещение электрода преобразователь вырабатывает соответствующий ток. Преобразовав значение тока можно получить значение отслеживаемой величины движения.
Рис.7. Ток, проходящий через преобразователь при пассивном демпфировании колебаний
Результаты доказывают наличие постоянной связи между электрической и механической частями системы и возможность моделей, созданных с помощью языка Modelica, выполнять как функции приводов, так и датчиков.
Заключение. Разработанные модели предлагается использовать при конструировании мехатронных модулей, проектировании датчиков, а также для исследования свойств различных типов преобразователей. Наличие библиотеки моделей преобразователей позволяет также подобрать оптимальные приводы для устройств с большим количеством перемещаемых деталей. Примером такого устройства является телескоп с адаптивной оптикой. В дальнейшем планируется найти больше параметров реальных систем для проверки адекватности каждой конкретной модели преобразователя.
Литература:
1. Janschek K. Systementwurf mechatronischer Systeme/ Janschek K. – Heidelberg: Springer, 2010. –842 с. 2. Колесов Ю.Б. Объектно-ориентированное моделирование сложных динамических систем. СПб.: Изд-во СПбГПУ, 2004. - 239 с.
3. Арайс Е.А., Дмитриев В.М.. Автоматизация моделирования многосвязных механических систем. М.: Машиностроение, 1987.- 240с.
4.Черных И.В. Simulink: среда создания инженерных приложений. М.:
ДИАЛОГ-МИФИ, 2003. – 496с.
5. Modelica - A Unified Object-Oriented Language for Physical Systems
Modeling. Language Specification. Version 2.0, July 10, 2002.
6. Modelica - A Unified Object-Oriented Language for Physical Systems
Modeling. Tutorial. Version 2.0, July 10, 2002.
7. Fritzson P. Introduction to Object-Oriented Modeling and Simulation with OpenModelica. 2006.-139 c.
8. Fritzson P. Principles of Object-Oriented Modeling and Simulation with Modelica 2.1.-Wiley-IEEE Press, 2006.- 939 c.
9. Charge control of parallel-plate, electrostatic actuators and the tip-in instability/ Seeger J. I., Boser B. E. // JOURNAL OF MICROELECTROMECHANICAL SYSTEMS, 2003.- №5. – С. 20–36.
