В статье приведены описание разработанной математической модели электрической системы содержащего парогазовой установкой ПГУ с асинхронными турбогенераторами со статорным возбуждением для анализа сложных электромеханических переходных процессов примере Талимарджан ЭС, с целью определения максимальных значений скручивающего момента и крутильных колебаний при анормальных режимах систем.
Ключевые слова: математическая модель, электроэнергетика, мощность, парогенераторы, асинхронные турбогенераторы, колебательные процессы, системы регулирования, дифференциальные уравнения.
Современные состояние развития электроэнергетики промышленно развитых стран, в том числе энергосистема Узбекистана характеризуется быстро растущим спросом на электрическую энергию и определенным отставанием ввода новых генерирующей мощностей. Основными причинами увеличения спроса является существенным изменением промышленной активности, масштабное жилищное строительство и существенное увеличение спроса в бытовом секторе.
В мировой практике изменение топливного баланса во всех промышленно развитых странах открывает широкое возможности энергетического использования на ряду с обычными газотурбинными установками (ГТУ) и паросиловыми установками (ПСУ), находит и установки комбинированные, рассчитанные на одновременное использование в качестве рабочих тел как пара, так и продуктов сгорания [1].
Используемые схемы парогазовых установок с высоконапорными парогенераторами и их модификации далеко не исчерпывают возможностей использования комбинированных паровых и газовых циклов в энергетике. Наряду с установками имеющие раздельные контуры потоков рабочих тел и предусматривающими наличие отдельных паровых и газовых турбин, известны установки контактного типа с непосредственным смещением пароводяного рабочего тела с продуктами сгорания.
Основой развития электроэнергетики является объединение электроэнергетических систем (ЭЭС) и использованием в них генераторов большой мощности. Механическая прочность элементов валопроводов мощных агрегатов снижается с ростом единичной мощности, а при некоторых анормальных режимах механические напряжения валопровода могут превысить допустимые. Электромеханические параметры синхронных генераторов традиционном исполнение ухудшены, и обеспечение устойчивости и надежности работы ЭЭС применяется различные системы регулирования, которые могут привести появлению электромеханическим колебаниям [2].
На наш взгляд наиболее эффективным мероприятием могут быть использования крупных асинхронных турбогенераторов со статорным возбуждением в современной электрической системы вызвано необходимостью дальнейшего повышения надежности генерирующего оборудования и эффективности функционирования энергосистем обосновано в [3]. С применением парогазовых установок (ПГУ) возникают вопрос использования асинхронных турбогенераторов со статорным возбуждением в газотурбинных установках.
В работе [4] приводятся результаты анализа сложных колебательным процессам в электрической системы содержащей синхронные турбогенераторы. Однако, моделирование сложных электромеханических переходных процессов, протекающих в асинхронном турбоагрегате не рассмотрены по настоящие время.
В данной работе рассмотрены составление математической модели электрической системы, содержащей ПГУ с асинхронными турбогенераторами со статорным возбуждения на примере Талимарджан ЭС с ПГУ мощностью 450 МВТ работающей через ЛЭП с напряжением 500 кВ параллельно с системой.
Для решения поставленной задачи составлено дифференциальные уравнения Парка — Горева элементов системы и дифференциальные уравнения относительного движения валопровода сосредоточенными массами. Уравнения элементов системы к координатной оси жестко связанной с роторам ведущего синхронного генератора.
Уравнения Парка — Горева асинхронного генератора в блоке с трансформатором:
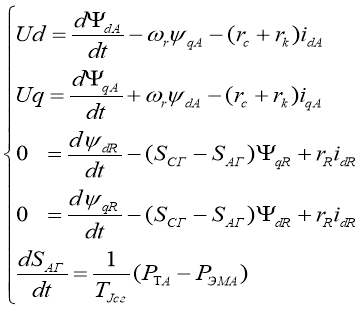(1)
Уравнения потокосцеплений АГ
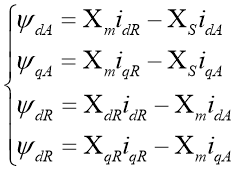(2)
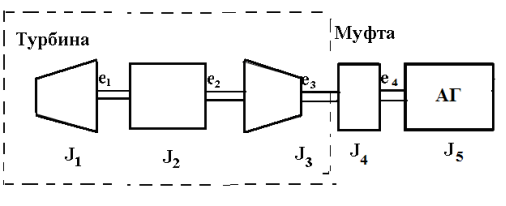
Рис. 1. Схема валопровода турбоагрегата АТГ-с — 330 и К-300–240–ЛМЗ для исследования электромеханических процессов и для анализа крутильных колебаний валопровода
Уравнения относительного движения вращающихся масс валопровода асинхронного турбоагрегата:
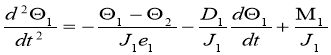
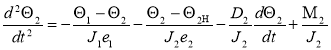
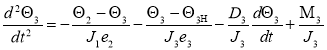(3)
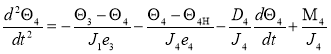
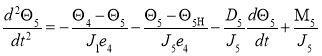
Θ — угол закручивания соответствующего участка вала;
J — полярный момент инерции массы;
е — податливость на кручению участка вала;
— коэффициент демпфирования крутильных колебаний соответствующего участка валопровода;
Мi — вращающей момент, приложенный к соответствующей массе;
Вращающие моменты агрегата
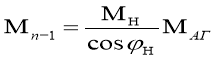(4)
(5)
Мн —номинальный вращающей момент генератора;
N — количества масс валопровода;
Мi — вращающей момент, приложенный к соответствующей массе;
— электромагнитный момент асинхронного генератора.
Валопровод турбоагрегата представляет собой упругую систему. Под воздействием периодически изменяющихся сил возникающих в результате анормальных режимов (короткие замыкание, асинхронные режимы, нарушение статической и динамической устойчивости) совершают вынужденные колебания. Эти колебания становится сильными в зоне резонансов возмущающих сил или моментов с собственными колебаниями системы. Вероятность возникновения опасных резонансов возрастает с увеличением быстроходности электрических генераторов, которые могут привести к поломки конструктивных деталей и элементов, и деталей фундамента.
Неравномерность крутящего момента вызывает неравномерность изменения угловой скорости вращения вала, т. е. то ускорение, то замедление вращения. Так как вал обладает упругостью и на нем размещаются массы (ЦВД. ЦСД, ЦНД, ротор генератора, соединительная муфта и возбудитель), то в каждом сечении вала будет своя степень неравномерности. то объясняется тем, что массы в одинаковый промежуток времени проходят разные углы и, следовательно, движутся с разными скоростями. Последние создает переменные закрутки в сечениях вала, что определяет его порочность.
Для расчетов валов на крутильные колебания необходимо кроме действующих моментов, знать жесткости участков каждого вала и значении моментов инерции масс, вращающихся вместе с валом. Из расчета определяются частоты, формы и амплитуды колебаний.
Уменьшение деформации в деталях, подверженных колебательным процессам, может происходить за счет использования асинхронного турбоагрегата как искусственного демпфирования. Задачи исследования в этом случае заключается в теоретическом и экспериментальном определении частот и форм собственных колебаний, анализе вынужденных колебаний и их устойчивости, в установлении возможности уменьшении амплитуд при резонансах, в выборе эффективных мер борьбы с ними в рабочем диапазоне оборотов агрегатов.
Массив бочки ротора асинхронного турбогенератора существеннодемпфирует электромеханические колебания генератора в связи ее электрической и магнитной симметрией.
В расчетах синхронных качаний можно исключить из схем замещения турбогенератора контуры с малыми постоянными времени (
с), что увеличивает сверхпереходные сопротивления турбогенератора.
Литература:
- Асаинов Д. Н. Короткие замыкания в электроэнергетической системе с газотурбинными установками малой мощности // Научно — исследовательские проблемы в области энергетики и энергосбережения. Материалы докладов Всероссийская конференция с элементами научной школы для молодежи. Уфа, 2–3 ноябрь 2010 г. Уфа. УГАТУ, 2010.
- Смоловик С. В., Кадхем Б. Т., Шхати Х. В. Демпфирование крутильных колебаний валопровода турбоагрегата с помощью АРВ // Научно — технические ведомости СПб ГПУ. 2007. № 4. С.202–206.
- Фазылов Х. Ф., Аллаев К. Р. Асинхронные турбогенераторы со статорным возбуждением и перспективы их применения // Изв. АН СССР. Энергетика и транспорт. 1985. № 2. С. 12 -18.
- Лукашов Э. С., Калюжный А. Х., Лизалек Н. Н., Соколов Ю. В. Моделирование и расчет длительных переходных процессов в сложных энергосистемах при больших небалансах мощности. Электричество. 1981, № 2.С. 7–10.
