Изучение и уточнение закономерностей поведения маятниковых систем является актуальным, т. к. во многих машинах, устройствах, приборах модели отдельных элементов могут быть сведены к маятнику с вибрирующей точкой подвеса.
Из исследований динамики маятниковых систем известно, что при определенном значении вибрационной скорости, устойчивость нижней точки маятника, в которой при отсутствии вибрации потенциальная энергия имеет минимальное значение, нарушается. В этом случае маятник занимает опрокинутое положение и устойчивым становится верхняя точка.
Известно, что движения физической модели маятника при вертикальной гармонической вибрации (рис. 1), описываются уравнением Матье в виде [1]:
для нормального маятника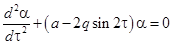 
, (1)
для опрокинутого маятника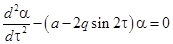 
, (2)
где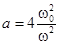 
, 
; 
; 
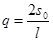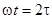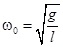– частота собственных колебаний маятника при неподвижной точке подвеса; 
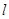– приведенное плечо физического маятника; 
, 
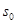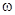- амплитуда и круговая частота вибрации; 
- малый угол отклонения от вертикали (10…15°).
Рис. 1. Физическая модель маятника при вибрации точки подвеса
Наиболее полное исследование уравнения Матье проведено в работе [1]. На рис. 2 показан фрагмент диаграммы устойчивости Айнса-Стретта для маятника при вибрации точки подвеса. На диаграмме заштрихованные области для положительных значений параметра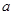 
соответствуют устойчивым нормальным положениям маятника. При отрицательных значениях параметра 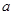заштрихованная область соответствует устойчивым опрокинутым положениям маятника.
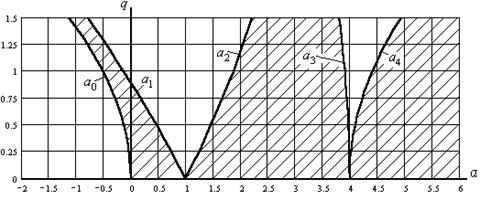
Рис. 2. Фрагмент диаграммы устойчивости Айнса-Стретта (для значений параметра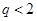 
)
При проведении экспериментальных исследований динамики физического маятника было отмечено, что в некоторых случаях при одних и тех же значениях 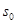и 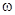наблюдается устойчивое состояние, как в нормальном, так и в опрокинутом положении, а также случаи, когда маятник неустойчив в нормальном положении, но устойчив в опрокинутом положении. На основании этого можно модифицировать диаграмму устойчивости Айнса-Стретта следующим образом, ²зеркально отобразив² область устойчивых движений маятника в опрокинутом положении, соответствующую отрицательным значениям параметра 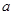, в область с положительными значениями параметра 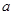. В результате диаграмма устойчивости Айнса-Стретта (рис. 3) показывает наличие трех характерных зон устойчивости физического маятника при вертикальной вибрации точки подвеса: зона устойчивого нормального положения, зона устойчивого нормального и опрокинутого положений, зона устойчивого опрокинутого положения. Причем последняя зона устойчивости появляется в области неустойчивых движений маятника.
При проведении экспериментов такая модификация позволяет значительно упростить планирование ожидаемых результатов экспериментов. По значениям параметров 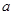и 
, при известных значениях приведенного плеча и частоты собственных колебаний маятника 
, можно однозначно судить об его устойчивых состояниях.
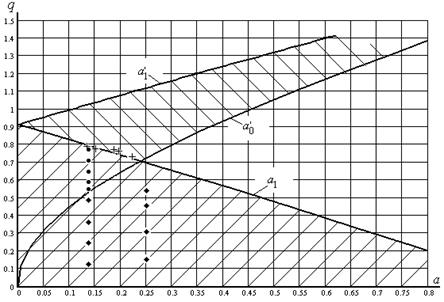
Рис. 3. Фрагмент модифицированной диаграммы устойчивости Айнса-Стретта
с результатами экспериментов:
w – устойчивое состояние маятника только в нормальном положении;
· – устойчивое состояние маятника в нормальном и опрокинутом положениях;
+ – устойчивое состояние маятника только в опрокинутом положении
На полученной диаграмме (рис. 3) особый интерес представляет кривая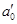 
. Это геометрическое место точек для соответствующих параметров 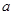и 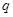, при котором наступает устойчивое опрокинутое положение. Из выражения 
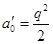, подставляя значения 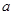и 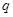, можно определить минимальную скорость вибрации, при котором наступает устойчивое опрокинутое положение в виде
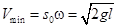. (3)
При скорости вибрации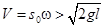 
наступает устойчивое опрокинутое положение маятника. Кривая 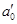по своей сути представляет кривую значений минимальной скорости вибрации, при которой наступает устойчивое опрокинутое положение.
Из данного выражения можно получить основное условие динамического равновесия. Для этого возведем в квадрат выражение (3), и умножим, справа и слева на массу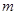 
маятника, в результате получим
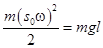. (4)
Левая часть представляет собой кинетическую энергию, сообщаемую маятнику вибрацией точки подвеса, а правая часть потенциальную энергию маятника в верхнем положении в поле сил тяжести.
Следовательно, в опрокинутом положении маятника алгебраическая сумма его кинетической и потенциальной энергий будет равна нулю. Иными словами, верхнее положение будет устойчивым динамическим состоянием равновесия маятника, т. к. его потенциальная энергия будет уравновешиваться кинетической энергией, обусловленной вибрацией точки подвеса.
Определим динамические силы, действующие на маятник при вибрации точки подвеса в нормальном, опрокинутом положении, а также в случае, когда маятник совершает колебания в плоскости горизонта.
На рис. 4, а изображена диаграмма сил, действующих на массу 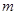физической модели маятника, который совершает колебания в плоскости горизонта (горизонтальный маятник). Такое расположение позволяет исследовать влияние вибрации на маятник без учета действия силы тяжести.
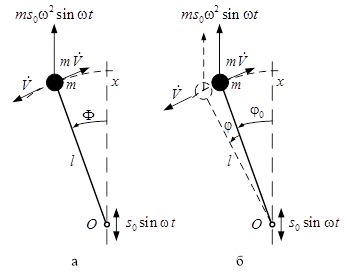
Рис. 4. Горизонтальный маятник под действием гармонической вибрации
Выражение результирующей силы относительно точки подвеса 
, получаемое путем проектирования сил на касательную к траектории движения массы , имеет вид
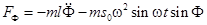. (5)
Экспериментальные исследования показывают, что, при некотором значении частоты 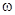(при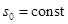 
), маятник устанавливается по некоторому направлению, определяемому углом 
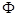, и совершает относительно данного положения колебания малой амплитуды и с частотой, намного меньшей частоты вибрации 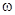. Угол 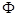может быть представлен следующим выражением 
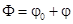(рис. 4, б), где 
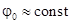(т.е. медленно меняющаяся величина); 
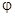- малые угловые колебания относительно устойчивого положения, определяемого 
.
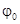В результате выражение (5) запишется в виде
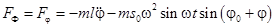. (6)
Используя метод, изложенный в работах [2, 3], получаем следующее выражение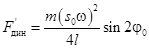 
(полное описание преобразований приводится в [4]).
Или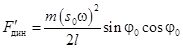 
. (7)
На рис. 5 показана осредненная по быстрому времени проекция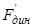 
на касательную к относительной траектории переменной силы инерции от вибрации основания, которая при принятых приближениях описывается выражением (7).
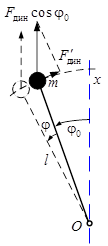
Рис. 5. Динамическая сила, действующая на маятник,
совершающий колебания в плоскости горизонта
Таким образом, на маятник, совершающий колебания в плоскости горизонта, действует динамическая (вибрационная) сила
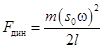. (8)
Из (8) видно, что вибрационная сила пропорциональна кинетической энергии, сообщаемой маятнику вибрацией подвеса, и обратно пропорциональна плечу маятника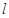 
.
Аналогично можно определить суммарную величину внешних сил, действующих на маятник по касательной к траектории движения массы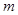 
в нормальном и опрокинутом положении:
для нормального маятника
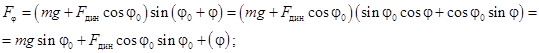(9)
для опрокинутого маятника
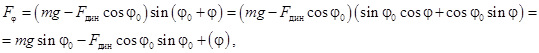(10)
где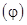 
– малая величина.
Выражение (8) позволяет заменить действие вибрации подвеса маятника динамической (вибрационной) силой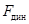 
. В результате замены в поле силы тяжести можно рассматривать модель маятника с неподвижной опорой (рис. 6), на которую действуют две силы: сила тяжести, направленная по вертикали места и динамическая сила, направленная по оси маятника.
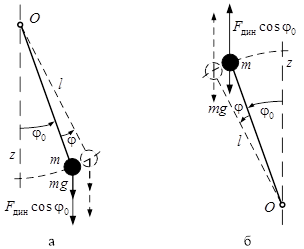
Рис. 6. Динамическая сила, действующая на маятник:
а – нормальное положение; б – опрокинутое положение
В результате дифференциальное уравнение такой системы при малых угловых колебаниях около соответствующего положения динамического равновесия будет описываться дифференциальным уравнением с постоянными коэффициентами, что значительно упрощает математическое описание системы.
Частоты собственных колебаний маятника (медленные осцилляции относительно положения ) для нормального и опрокинутого положения при гармонической вибрации точки подвеса, при отклонениях оси маятника от оси 
на малый угол 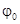, с использованием динамической силы можно определить из следующих выражений:
для нормального маятника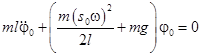 
, (11)
для опрокинутого маятника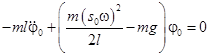 
, (12)
или
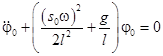, (13)
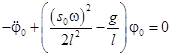. (14)
Уравнения (13) и (14) описывают свободные колебания маятника с соответствующими частотами, определяемыми выражениями при 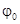. В уравнениях обозначим: 
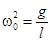- квадрат частоты собственных колебаний маятника при неподвижной точке подвеса; 
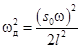- квадрат частоты собственных колебаний маятника, когда действует только вибрационная сила (колебания маятника в плоскости горизонта).
Полученные выражения подтверждают известный из экспериментов результат об изменении частоты собственных колебаний маятника, при вибрирующей точке подвеса - в нормальном положении маятника частота собственных колебаний увеличивается, а опрокинутом - уменьшается.
На рис. 7, 8 представлены зависимости изменения частоты собственных колебаний маятника от виброскорости в нормальном и опрокинутом положении, полученные путем физического (+) и математического (–) моделирования.
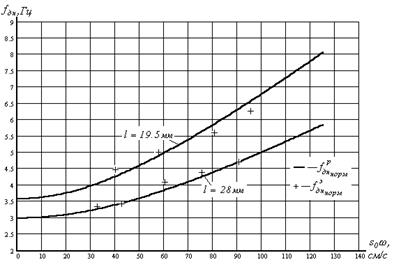
Рис. 7. Изменение частоты собственных колебаний маятника
от виброскорости в нормальном положении
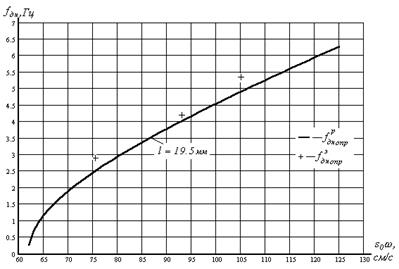
Рис. 8. Изменение частоты собственных колебаний маятника
от виброскорости в опрокинутом положении
Представленные в работе положения позволяют проводить описание динамической устойчивости маятниковых систем при вибрационном воздействии с помощью достаточно простых закономерностей.
Литература
1. Мак-Лахлан Н.В. Теория и приложения функций Матье. – М.: ИЛ, 1953. – 475 с.
2. Капица П.Л. Динамическая устойчивость маятника при колеблющейся точке подвеса // Журнал экспериментальной и теоретической физики. – 1951, т. 21, в. 5. - с. 588 - 597.
3. капица П.Л. Маятник с вибрирующим подвесом // Успехи физических наук. – 1951, т. 64, в. 1. - с. 7 - 20.
4. Глазачев А.В., Копытов В.И. Динамическая (вибрационная) сила, действующая на маятник при гармонической вибрации точки подвеса. VII обл. конференция молодых ученых, аспирантов и студентов. «Современная техника и технология», Томск, 2001. - с. 129 - 131.
