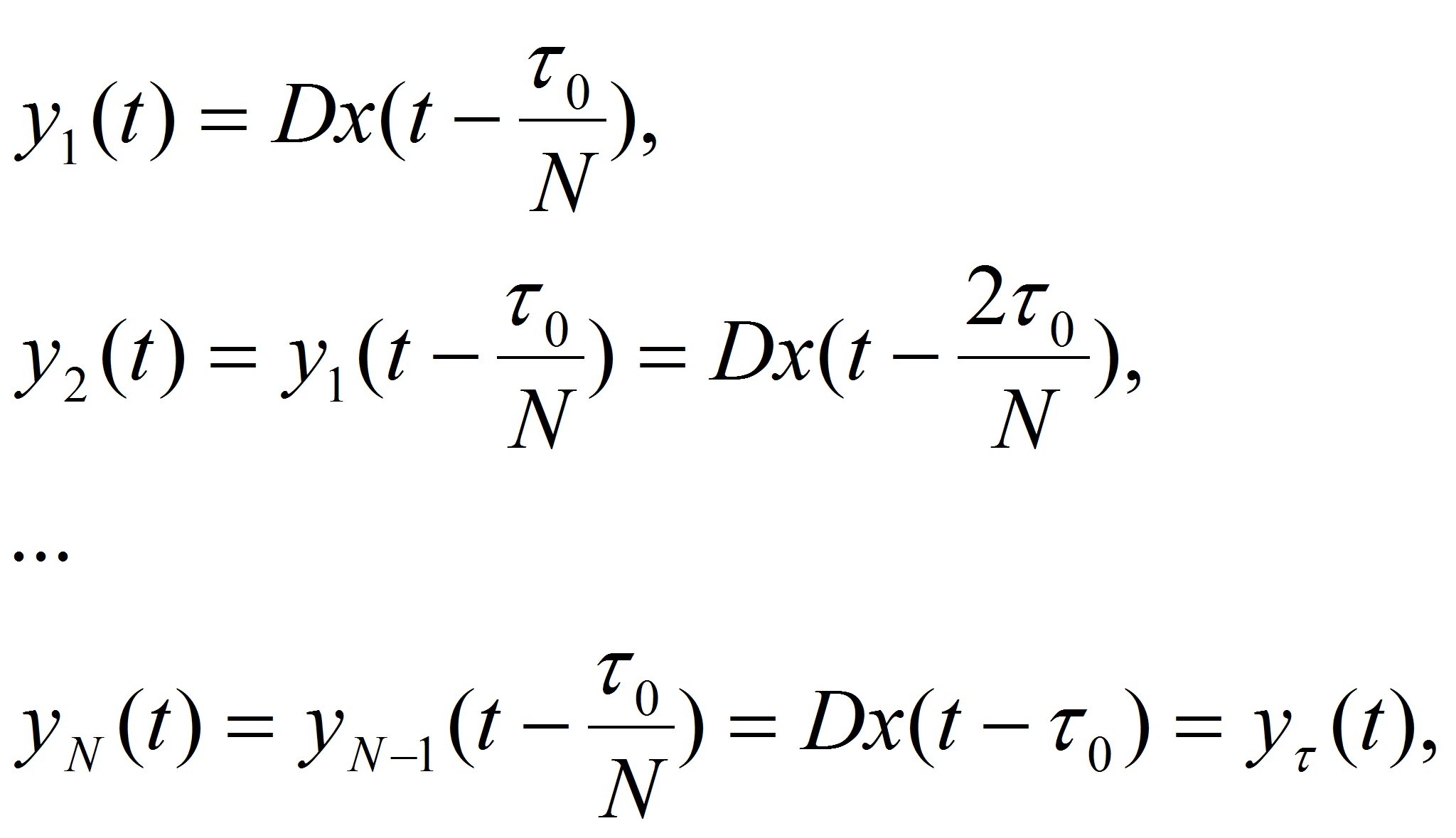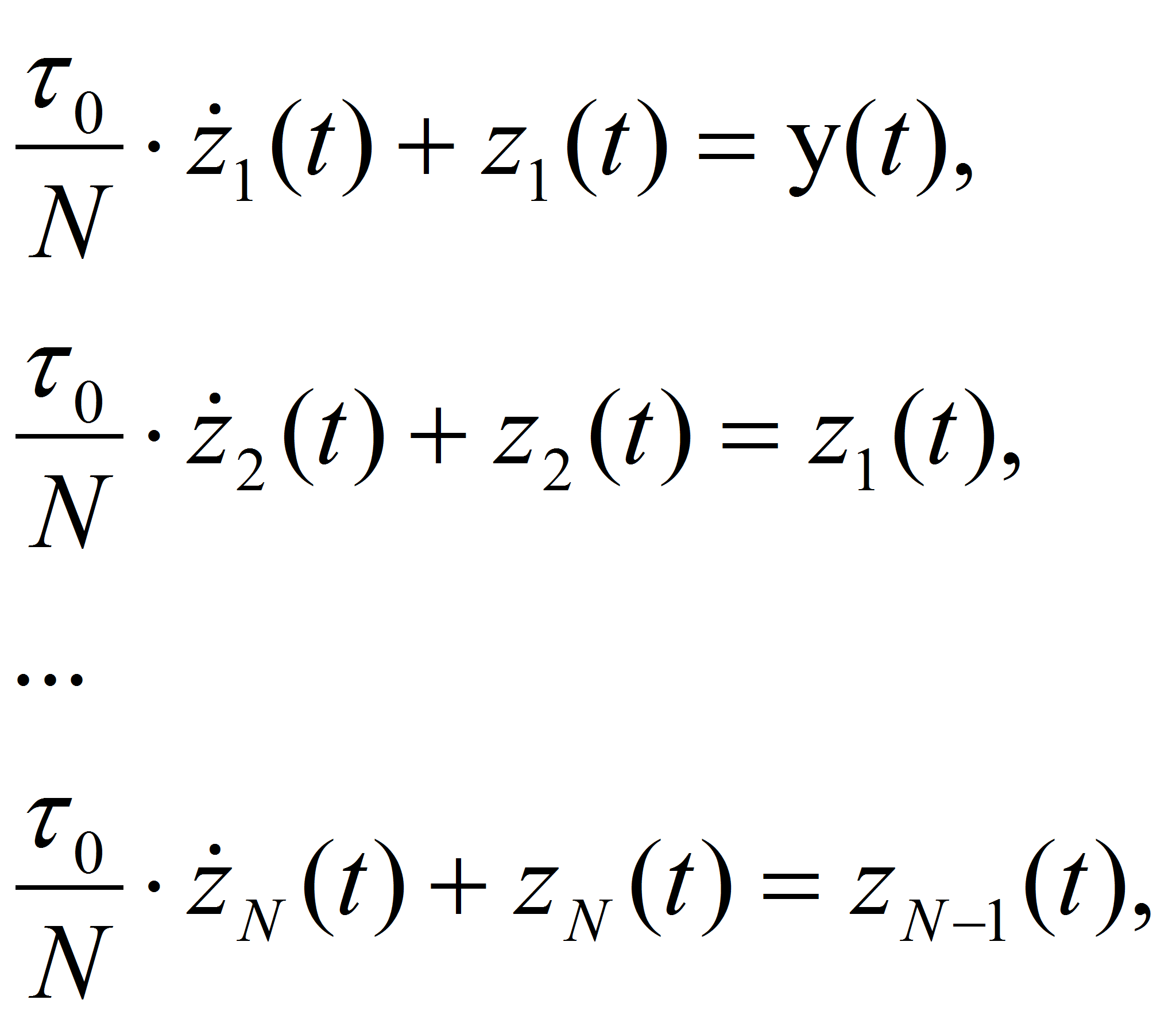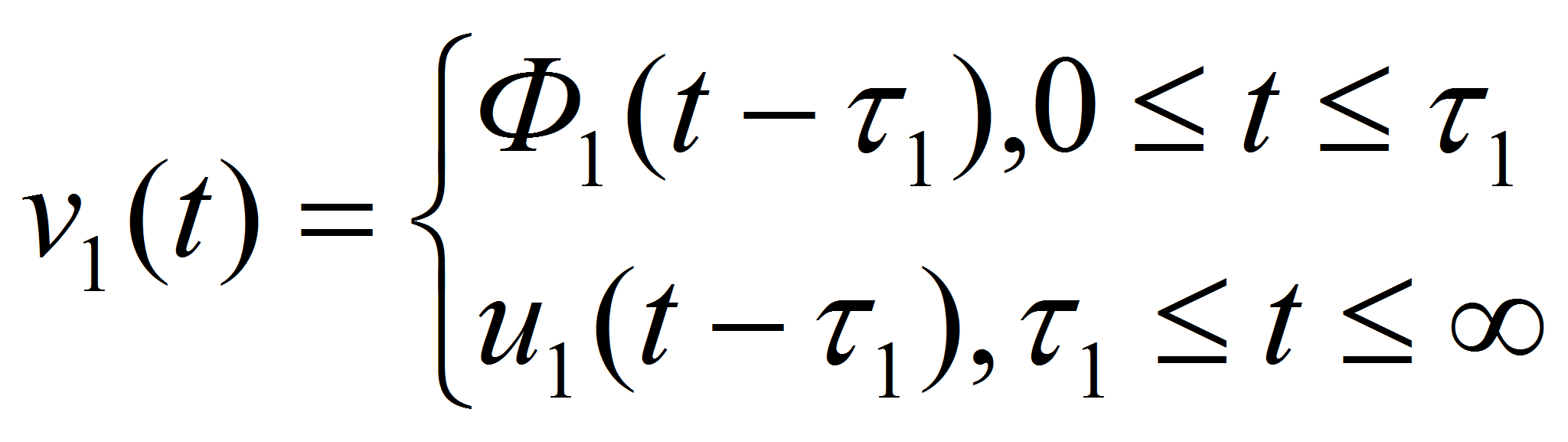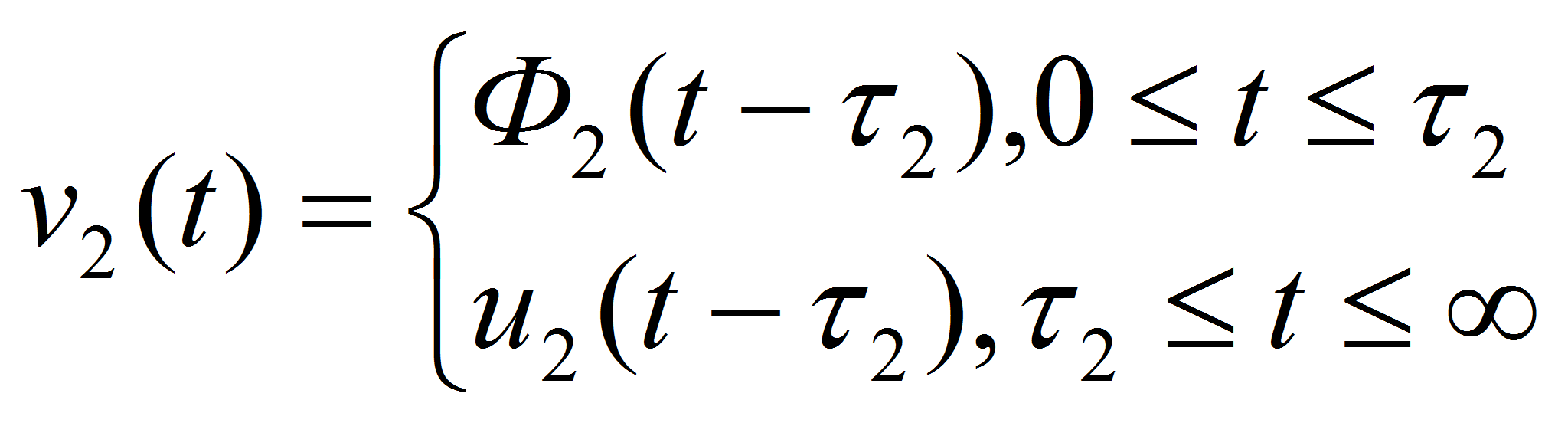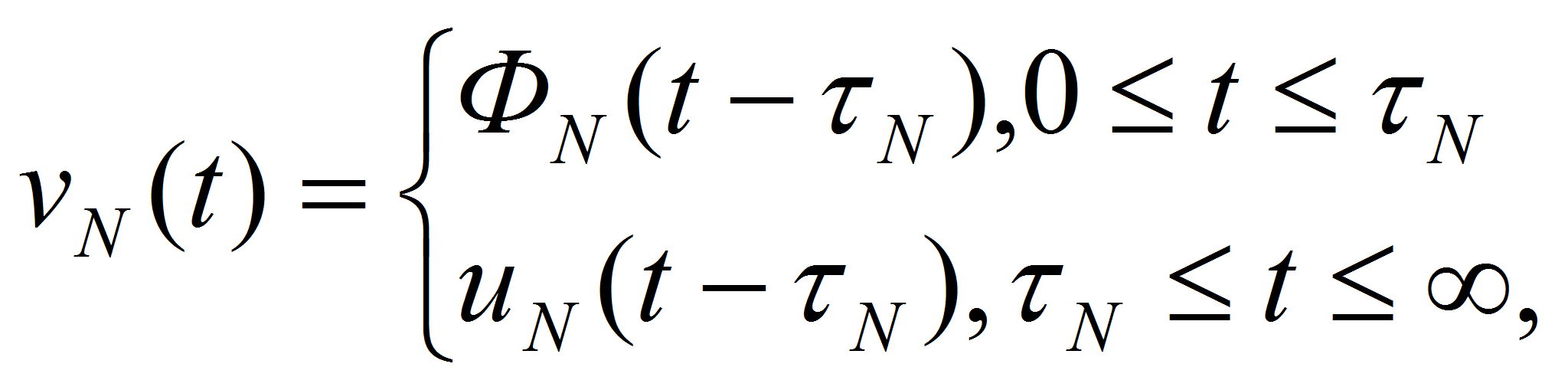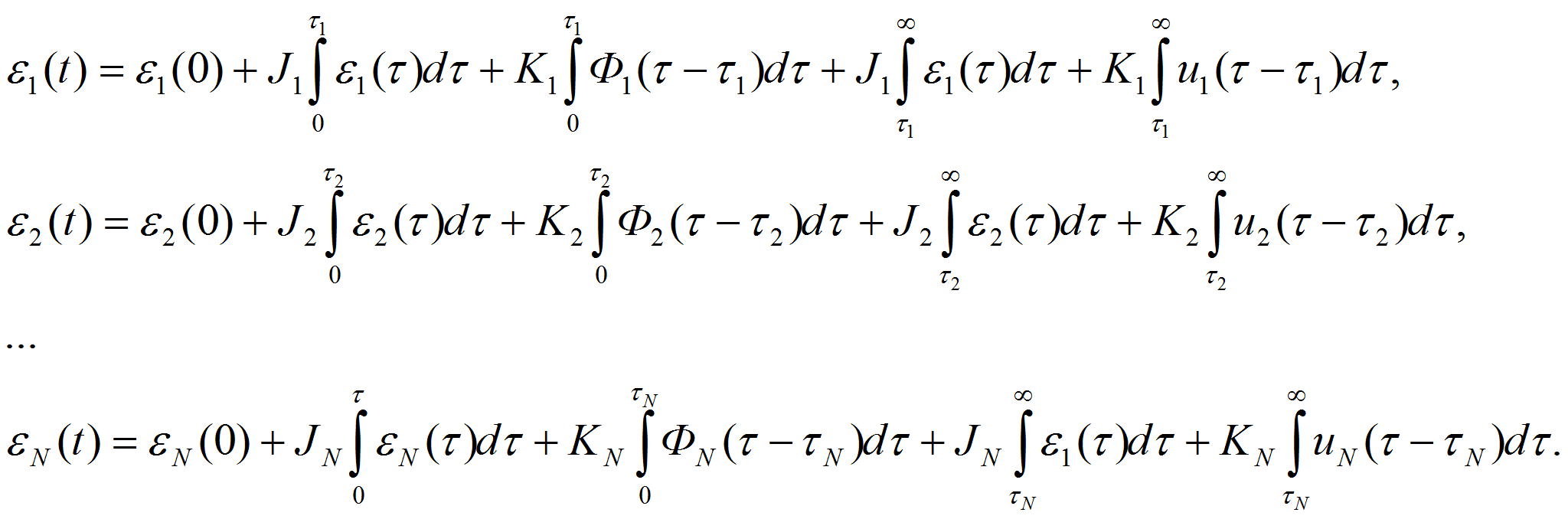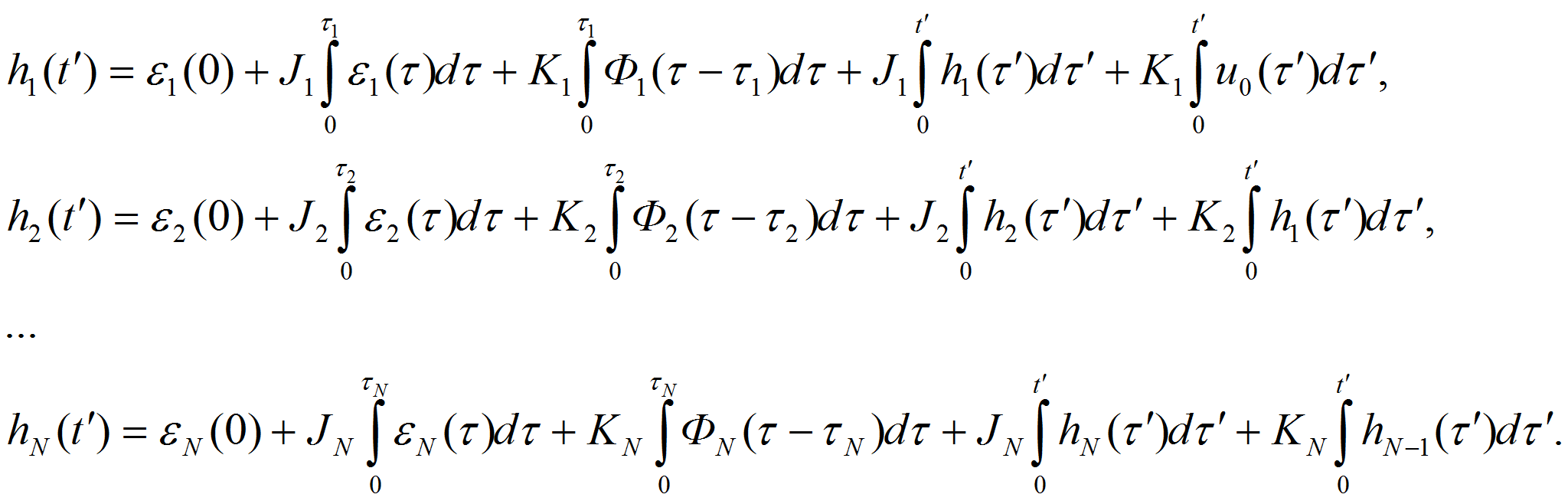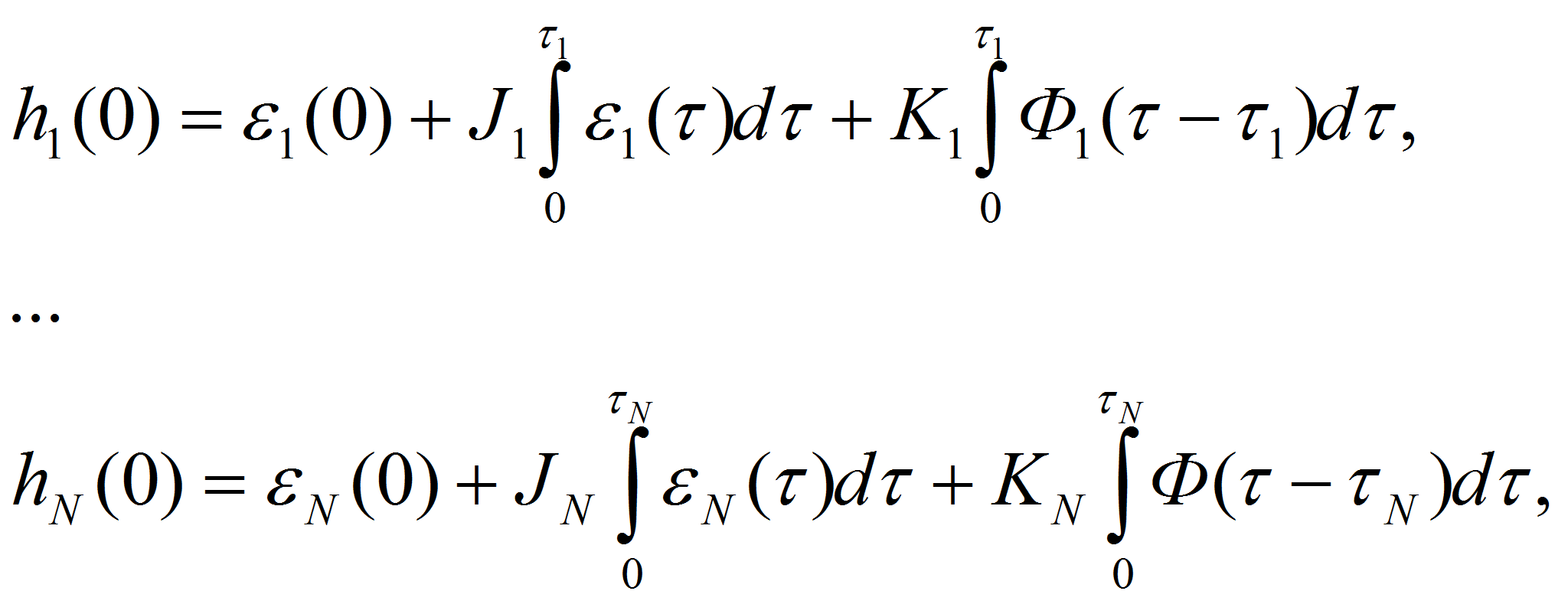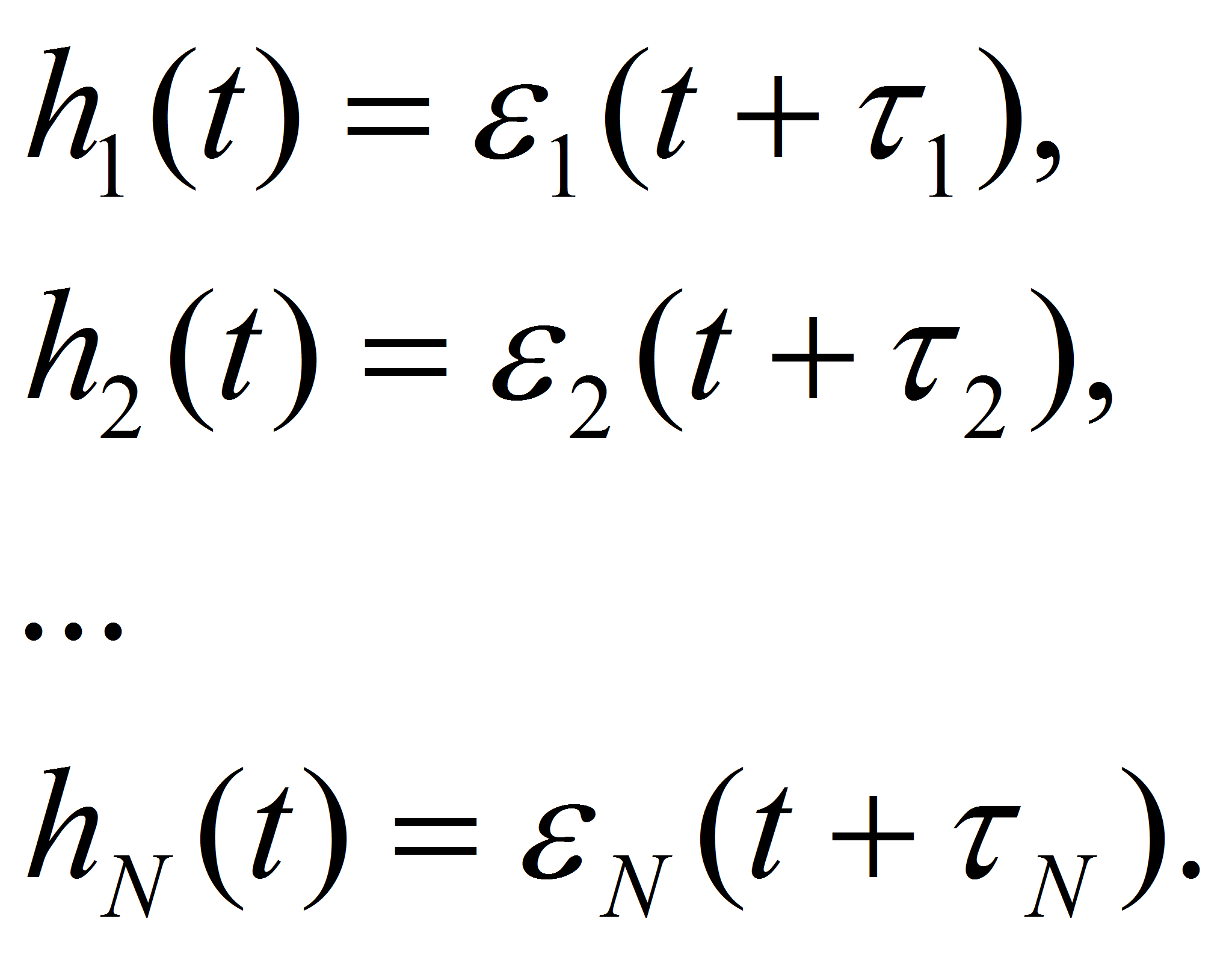Синтез наблюдателя для системы с запаздыванием по выходным переменным

1. Введение

Разработка алгоритмов автоматического управления часто осложнена наличием запаздывания в модели объекта управления. Запаздывание может быть как по входу (система управления реагирует с запаздыванием на входные воздействия), так и по выходу (система выдает с запаздыванием выходные сигналы).

Одним из наиболее распространенных способов управления такими процессами является создание модели объекта без запаздывания. При этом если задача наблюдения для системы с запаздыванием по входу решена [1], то аналогичная задача с запаздыванием по выходу связана с определенными трудностями ввиду ненаблюдаемости как вектора состояния, так и вектора выходных переменных в текущий момент времени.

Предлагается решение задачи наблюдения для системы с запаздыванием по выходным переменным с использованием блочного метода.

2. Постановка задачи

Рассмотрим случай запаздывания по выходным параметрам:

(1)

где , - вектор состояний, управления и выходного сигнала соответственно, время запаздывания, пара матриц - управляемая и пара матриц наблюдаемая. Для измерения доступен только вектор

Ставится задача наблюдения вектора состояния системы (1).

Если бы была известна величина , то использование наблюдателя состояний вида где привело бы к решению задачи. Однако вектор недоступен для измерения, так как выход системы представляет собой реакцию на предыдущее состояние.

В работе ставится задача восстановления вектора выхода в текущий момент времени.

3. Процедура восстановления вектора выхода в текущий момент времени

Рассмотрим задачу компенсации запаздывания по выходным переменным.

Введем в рассмотрение апериодическое звено с постоянной времени, равной времени запаздывания на вход которого поступает величина y(t). Установим соответствие между y(t) и выходом z(t) апериодического звена:

(2)

Оценим разность:

(3)

при этом полагая

Рассмотрим производную :

(4)

Выражение (4) можно представить в виде:

, (5)

где

_{Допустим, функция Dx(t) удовлетворяет условию Липшица с постоянной М. Тогда:}

(6)

Представим исходную систему как последовательное соединение N элементарных звеньев с запаздыванием эквивалентное исходному звену с запаздыванием [2]:

(7)

где выходные величины соответствующих элементарных звеньев. На вход каждого i-го звена подается выходной сигнал предыдущего, также предусмотрена возможность подачи любого управляющего воздействия.

Сделаем аналогичное представление для апериодического звена запаздывания, разбив его на N элементарных апериодических звеньев с постоянной времени соединенных последовательно. По аналогии с выражением (2) можно записать:

(8)

где выходные величины соответствующих элементарных апериодических звеньев.

Рассмотрим разность

(9)

Согласно (7)

(10)

Как следует из (18),

_{Таким образом, при возрастании числа апериодических звеньев, выход N-го звена сходится равномерно по дискретизации к выходу реальной системы с запаздыванием. Однако рассогласование никогда не будет тождественно равно нулю при конечном N (что имеет место в реальных системах).}

Для достижения сходимости необходимо ввести обратную связь по величине рассогласования

Подадим на вход каждого i-го звена системы (8) управляющее воздействие так, чтобы:

(11)

где - время запаздывания каждого апериодического звена относительно предыдущего, - время запаздывания каждого апериодического звена относительно выхода, - время запаздывания первого звена относительно выхода; пара матриц - управляемая и наблюдаемая.

Управляющие воздействия выбраны в виде:

(12)

_…

где - определены ниже.

_{После интегрирования система (11) принимает вид:}

Сделаем замену переменной i – номер звена. Введем в рассмотрение новый вектор состояния

. (13)

Заменим переменную интегрирования и получим следующую систему уравнений:

(14)

После дифференцирования по времени получаем:

с начальными условиями:

_где

_{Представим систему (14) в векторной форме:}

(15)

где - управляемая и пара матриц.

Оптимальное по быстродействию управление системой (15) находится методом поверхности переключений и в общем случае имеет вид:

(16)

Для определения оптимального управления системой (11) необходимо выразить координаты вектора через координаты вектора . С помощью такого оптимального управления будет достигнуто и, в свою очередь, сходимость выхода цепочки апериодических звеньев к выходу реальной системы

_{Таким образом, удалось восстановить вектор выходных переменных в текущий момент времени и решить поставленную задачу наблюдения.}

Литература:

1. Краснова С.А., Уткин В.А. Каскадный синтез наблюдателей состояния динамических систем. – М.: Наука, 2006. с. 245-250.

2. Громов Ю.Ю., Земской Н.А. Системы автоматического управления с запаздыванием. – Тамбов: Изд-во ТГТУ, 2007.

3. Furukawa T., Shimemura E. Predictive control for systems with delay// Int. J. Control. 1983. Vol. 37. N 2. p.307-312.

4. Колмановский В. Б., Носов В. Р. Устойчивость и периодические режимы регулируемых систем с последействием. – М.: Наука, 1981.