Обобщенная марковская игра «Большой матч»



Марковская игра «Большой матч» изучена в обобщенной форме.

1. Обобщенный большой матч. Марковская игра «Большой матч», как представитель марковской игры с конечным множеством состояний и конечными множествами решений игроков и критерием предельного среднего выигрыша первого игрока, изучена в работах [1–7]. Представляет интерес, так называемая, обобщенная марковская игра «Большой матч» или «обобщенный большой матч» (сокращенно ОБМ), задаваемой тремя игр-компонентами:

(1)

где матрица Г_i (i = 1, 2, 3) представляет собой i-е состояние игры ОБМ; a, b. с  числа. В случае a = с = 1, b = 0 имеет место игра «Большой матч»

Процесс разыгрывания игры ОБМ состоит в следующем. На первом шаге в состоянии Г₁ игроки I и II независимо друг от друга выбирают строку i и столбца j соответственно. В результате складывается ситуация (i, j). После чего согласно элементу γ_ij формальной матрицы Г₁ определяется выигрыш игрока I и следующее состояние игры. Так, например, при ситуации (1, 1) γ₁₁ = a + Г₁ и игрок II платит игроку I aединицу и следующим состоянием игры будет снова Г₁. Состояния Г₂ и Г₃ являются поглощающими, ибо, попадая в одно из них, игра останется в нем навсегда. На каждом шаге игры игроки оглашают свои решения с помощью монеты. Показ герба (Г) означает, что игрок I (II) выбрал первую строку (первый столбец), а показ решетки (Р)— вторую строку (второй столбец).

Введем обозначения: ξ_n (η_n) — решающая функция, представляющая собой вероятность выбора решения «герб» игроком I (II) на n-мшаге игры; π = (ξ₁, ξ₂, …, ξ_n, …) — стратегия игрока I; φ = (η₁, η₂, …, η_n, …) — стратегия игрока II; ξ^∞ = (ξ, ξ, …, ξ, …), η^∞ = (η, η, …, η, …) — стационарные стратегии игроков I и II, соответственно; — средний суммарный выигрыш игрока I за n шагов при стратегиях игроков π и φ и начальном состоянии Г₁; — средний выигрыш игрока I за один шаг в nшаговом игре при π и φ и начальном состоянии Г₁. Стратегии игроков π^* и φ^* оптимальны, если справедливо двойное неравенство для всех n≥ 1 и произвольных π и φ.

2. Целевая функция игры ОБМ вклассе стационарных стратегий. Представим в явном виде целевую функцию 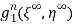. Согласно игр-компонентам (1) игра ОБМ, как марковская игра, характеризуется следующими данными

Состояние	Ситуация	Вероятность перехода			Выигрыш
i	(k, r)
1	(1, 1) (1, 2) (2, 1) (2, 2)	1 0 1 1	0 1 0 0	0 0 0 1	a 0 0 0
2	(1, 1)	0	1	0	b
3	(1, 1)	0	0	1	c

Пусть игра ОБМ находится в состоянии 1. Иначе говоря, пусть разыгрывается игровая компонента Γ₁. При стратегиях игроков (ξ, 1 ξ) и (η, 1 η) вероятность остаться в игровой компоненте Γ₁ равна ξη + (1ξ)η = η. Вероятности перехода из Γ₁ в Γ₂ и Γ₃ соответственно равны ξ(1η) и (1ξ)(1η). Следовательно, матрица P(ξ, η) имеет вид

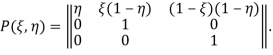
Отсюда получим матрицу вероятностей перехода за n шагов и вектор ожидаемых выигрышей игрока I:

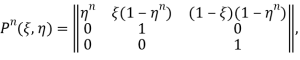
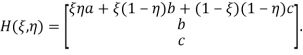
Отсюда следует, что

= σ_n [ξηa + ξ(1 — η)b + (1 — ξ)(1 — η)c] + ξ(1 — σ_n)b + (1 — ξ)(1 — σ_n)c,

где σ_n= (1 + η + η² + … + η^{n — 1}) / n.

Условимся обозначать через σ_∞ величину σ_n. Тогда, целевая функция игры ОБМ с бесконечным числом шагов в классе стационарных стратегий имеет вид

= σ_∞ [ξηa + ξ(1 — η)b + (1 — ξ)(1 — η)c] + ξ(1 — σ_∞)b + (1 — ξ)(1 — σ_∞)c. (2)

3. Метод последовательных приближений. Оптимальные стратегии игроков π^* и φ^* и значение 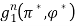игры ОБМ с конечным числом шагов n могут быть определены с помощью модифицированного функционального уравнения преобразования цен(см. [4, 5]), которое для игр-компонент (1) принимает вид:

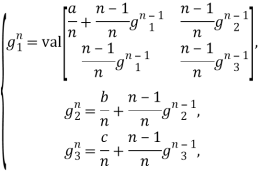(3)

где i = 1, 2, 3; n≥ 1.

Из 2-го и 3-го уравнения получаем Подставив эти значения в 1-ое уравнение системы (3), имеем

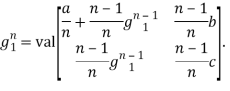(4)

Решая эту 22-игру (см. [8, c. 45]), находим значение игры ОБМ и оптимальные стратегии игроков для конечного n.

Рекуррентные соотношения (3) могут быть использованы для решения ОБМ с бесконечным числом шагов. Именно, при n (4) дает значения игры , а ε-оптимальные стационарные стратегии игроков достигаются за конечное число шагов n.

Между тем, специфическая особенность игры ОБМ позволяет решить данную задачу более простим путем. Так, положив в (4) ε = 1/n и записав вместо величины искомое ее предельное значение получим уравнение относительно

(5)

Решая эту 22-игру, находим значение игры ОБМ и ε-оптимальные стационарные стратегии игроков:

(6)

(7)

(8)

Заметим, что если в (2) подставить и , то получится

Следует отметить, что при a = с = 1, b = 0 получим результаты, соответствующие игру «Большой матч» (см. [47]):

4. Метод аппроксимации ОБМ игрой спереоценкой. Для изучения и решения ОБМ с бесконечным числом шагов наиболее подходящим методом является аппроксимация ОБМ соответствующей игрой с переоценкой. В этом случае функция выигрыша имеет вид 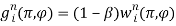, где  [0, 1) коэффициент переоценки.

Исходя из результатов, изложенных в [9] для данных игр-компонент (1) имеют место следущие рекуррентные соотношения

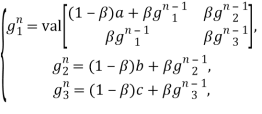(9)

где i = 1, 2, 3; n≥ 1.

Рекуррентные соотношения (9) позволяют решить игру ОБМ с переоценкой. Именно, при n (9) дает значения игры и -оптимальные стационарные стратегии игроков . Здесь, записав вместо величин искомые их предельные значения имеем

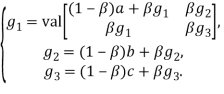(10)

Из 2-го и 3-го уравнения получаем . Подставив эти значения в 1-ое уравнение системы (10), имеем

Здесь, если положить ε = 1 , то данное уравнение принимает вид

которое ничем не отличается от уравнения (4).

Эти факты показывают насколько тесно связаны рекуррентные соотношения (3) и (9).

5. ОБМ  принятия решений вусловиях риска. Вслучае, когда a и b больше с игра ОБМ имеет тривиальное решение. В этом случае, в игровой компоненте Γ₁ 1-я строка доминирует 2-ую строку и игрок I с вероятностью 1 принимает решение Г (ξ = 1). Тогда игрок II выбирает решение Г (η = 1) и цена игры 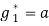, если ab;  решение Р (η = 0) и цена игры 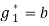, если a>b. Так же тривиально решается случай, когда a и b меньше с.

Заслуживает внимание случай, когда одно из чисел а и b больше с, а другое меньше с. Пусть a≥c, а b<c. В этом случае решение Г игрока II связано с определенным риском. Здесь, игрок II может принимать решение Р и игра переходит во 2-ое состояние и игрок II платит игроку I b единиц (если b отрицательно, то игрок I платит игроку II b единиц) на каждом шаге игры.

Характерной особенностью игры ОБМ является то, что только при решении Р игрока II игра может покинуть состояние Γ₁. При разыгрывании игры ОБМ этим обстоятельством игрок II может воспользоваться разумным образом. Играв достаточно длительное время «герб» игрок II сначала изучает поведение игрока I, т. е. следит за статистикой W_n = m/n, где m число «гербов» принимаемых игроком I за n шагов игры. Если W_n > (6), то игрок II наверняка будет выбрать «решетку» и выигрыш игрока будет меньше, чем цена игры (5). Если W_n, то решение «герб» остается неизменным на последующих шагах игры и выигрыш игрока II не больше, чем цена игры . Такая адаптивная стратегия игрока II вполне приемлема при разыгрывании игры ОБМ. При этом игроку II целесообразно воспользоваться методом принятия решений в условиях риска, изложенным в [10].

Конечно, лучше всего игроку II воспользоваться случайным механизмом, обеспечивающим ему проигрыш не больше, чем цена игры , аналогичным случайному механизму T(m, k), изложенному в [7]. Но этот вопрос является темой другой статьи. Здесь мы ограничиваемся рассмотрением двух частных случаев:

1) a = 2, b= 0, с = 1. Согласно (6)(8) .

Целевая функция (2) примет вид

= 2σ_∞ξ + (1 — ξ)(1 — σ_∞).

Здесь, при ξ = 1/3 независимо от значения σ_, при σ_ = 1/3 независимо от значения ξ. Так что, в случайном механизме T(m, k) дробь m/k может быть выбрана так, что m/kln3 с любой точностью. Тогда обеспечивается равенство σ_ = 1/3 с заданной точностью и случайный механизм T(m, k) может быть использован игроком II при разыгрывании рассматриваемой игры ОБМ.

2) a = 1, b= 0, с = 2. Согласно (6)(8) .

Целевая функция (2) примет вид

= σ_∞ξ + 2(1 — ξ)(1 — σ_∞).

Здесь, при ξ = 2/3 независимо от значения σ_, приσ_ = 2/3 независимо от значения ξ. Так что, в случайном механизме T(m, k) дробь m/k может быть выбрана так, что m/kln с любой точностью. Тогда обеспечивается равенство σ_ = 2/3 с заданной точностью и случайный механизм T(m, k) может быть использован игроком II при разыгрывании рассматриваемой игры ОБМ.

Литература:

1. Gillette D. Stochastic games with zero stop probabilities // Contributions to the Theory of Games. V.III / Dresher M. Princeton, Univ. Press., 1957. Ann. Math. Studies № 39.
2. Blackwell D. The big Matсh // STAM J. Appl / Math. 1970. № 19. Р. 473–476.
3. ИбрагимовА. А. Омарковскойигре«большойматч» // РАН. Автоматикаителемеха-ника. 2000. № 11. С. 104–113.
4. ИбрагимовА. А. Марковскиеигрыснесколькимиэргодическимиклассами // Укра-инскийматематическийжурнал. 2003. Т.55. № 6. С. 762–778.
5. ИбрагимовА. А. Существованиезначениявобщихмарковскихиграх // ИзвестияРАН. Теорияисистемыуправления. 2004. № 2. С.5–15.
6. ИбрагимовА. А. Оптимальныедействиясторонвбольшомматче // VI Междуна-роднаяконференция MMR 2009 —Математическиеметодывтеориинадежности (Москва, 22–29 июня 2009 г.). Расширенныетезисыдокладов. С. 256–260.
7. ИбрагимовА. А. Марковскаяигра«Большойматч»вклассестационарнқхстратегий // Журнал«Молодойученый»№ 4 (84), март, 2015 г. Москва. С. 4–7.
8. ДюбинГ. Н., СуздальВ. Г. Введениевприкладнуютеориюигр. М.: Наука, 1981. 336 с.
9. ИбрагимовА. А. Решениеобщеймарковскойигрыпутемаппроксимацииееигройспереоценкой // Журнал«Молодойученый»№ 13 (117), июль-1, 2016 г. Москва.
10. ИбрагимовА. А. Построениефункцииполезностидлястатистическойзадачире-шениясвходнойплатой // Узбекскийжурнал«Проблемыинформатикииэнергетики». 1997. № 5. С. 3–8.