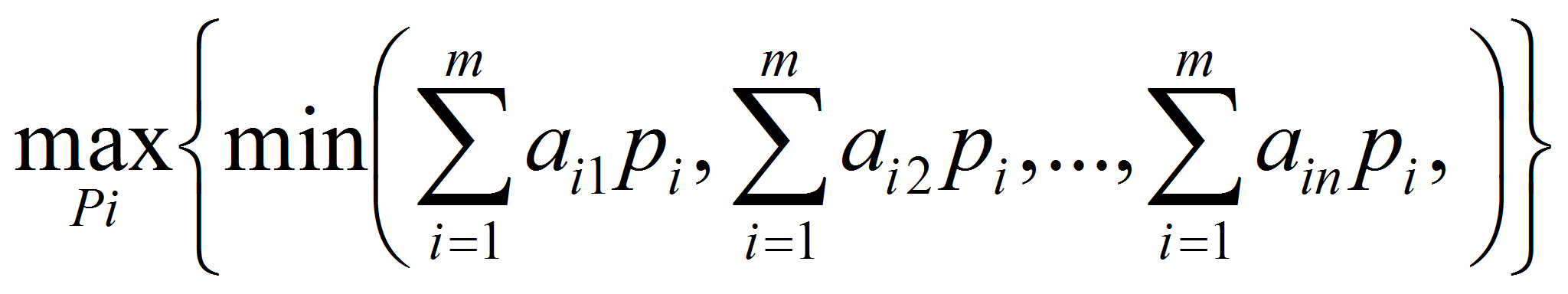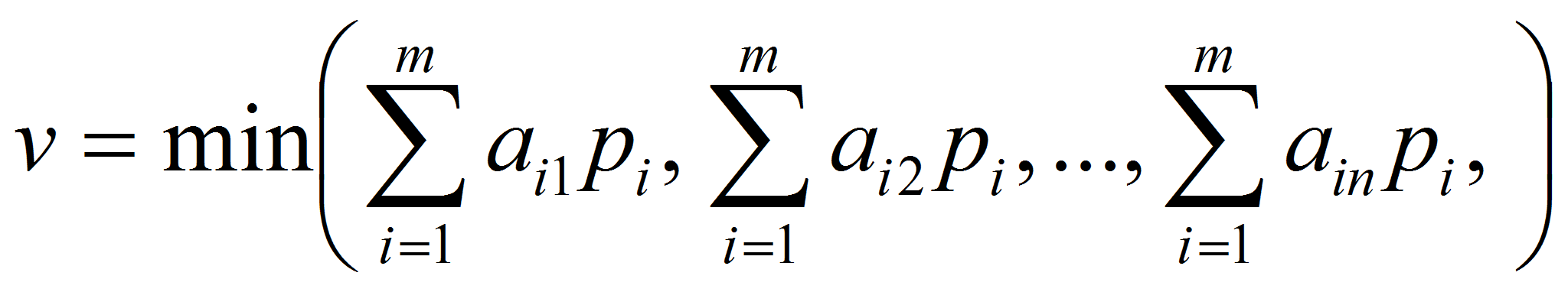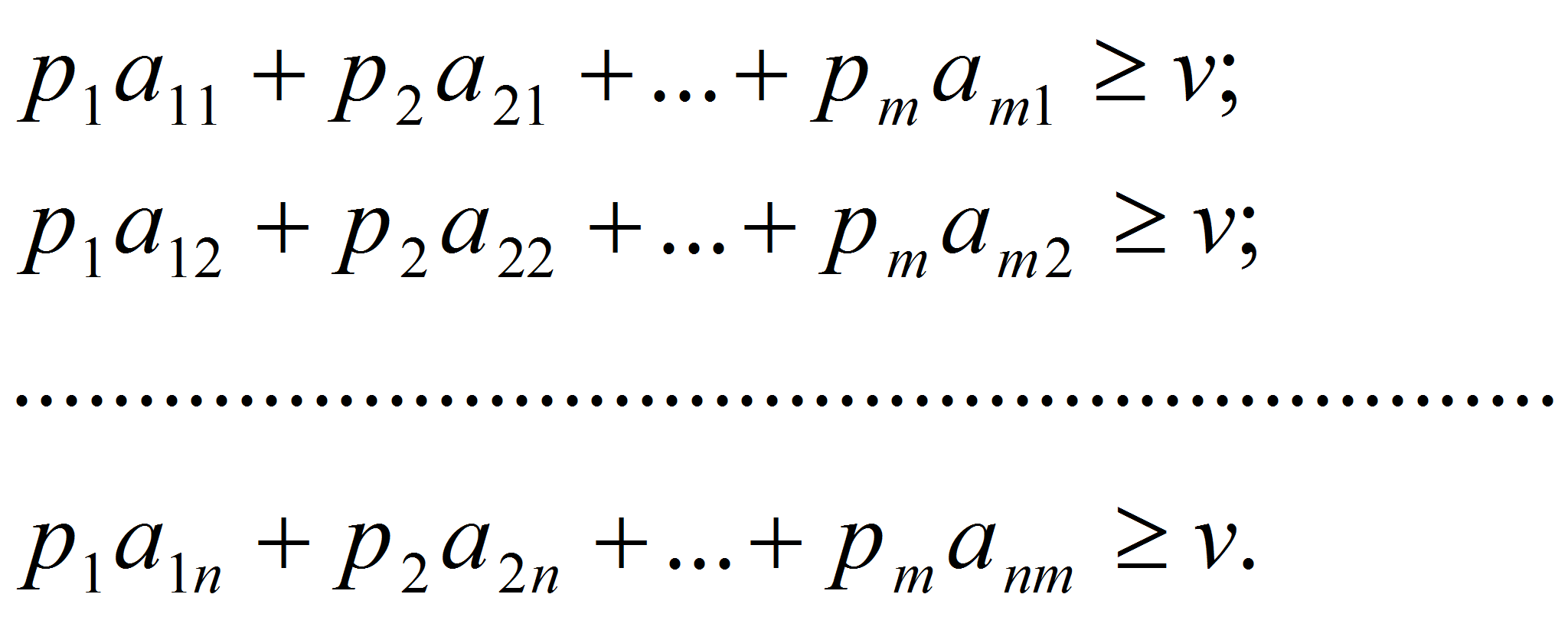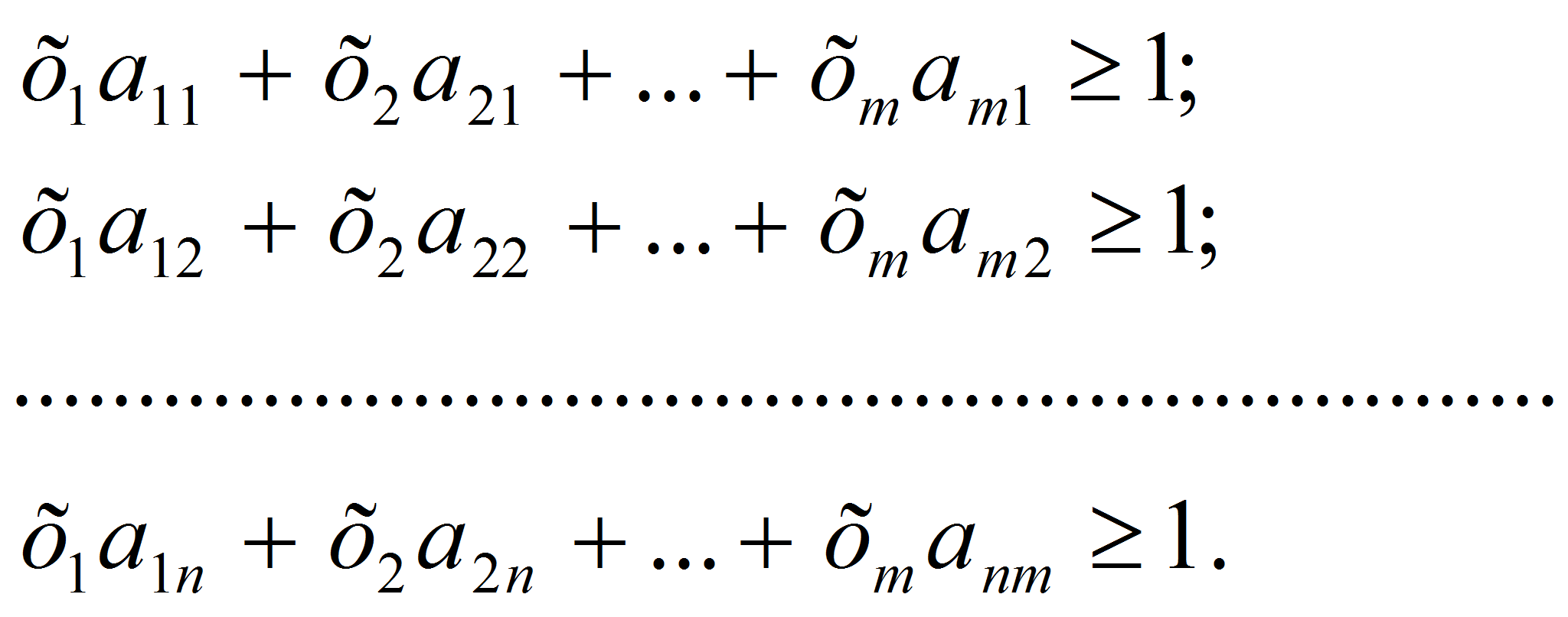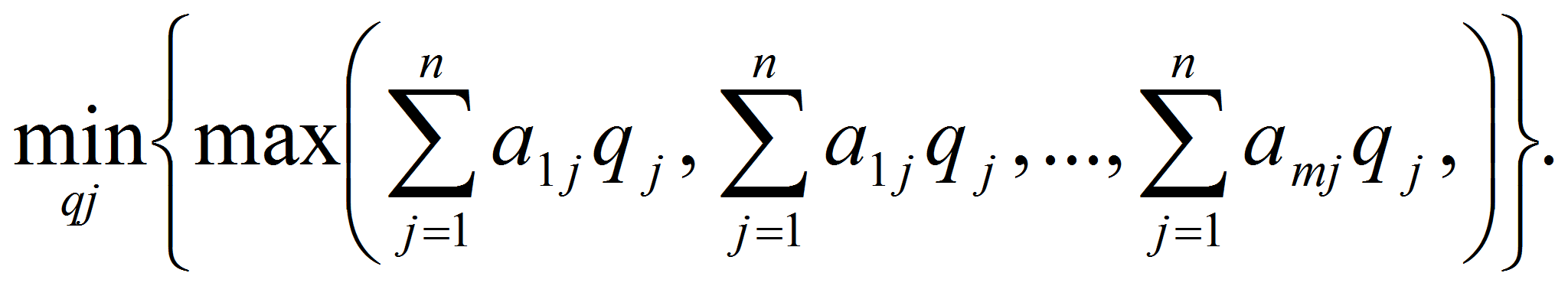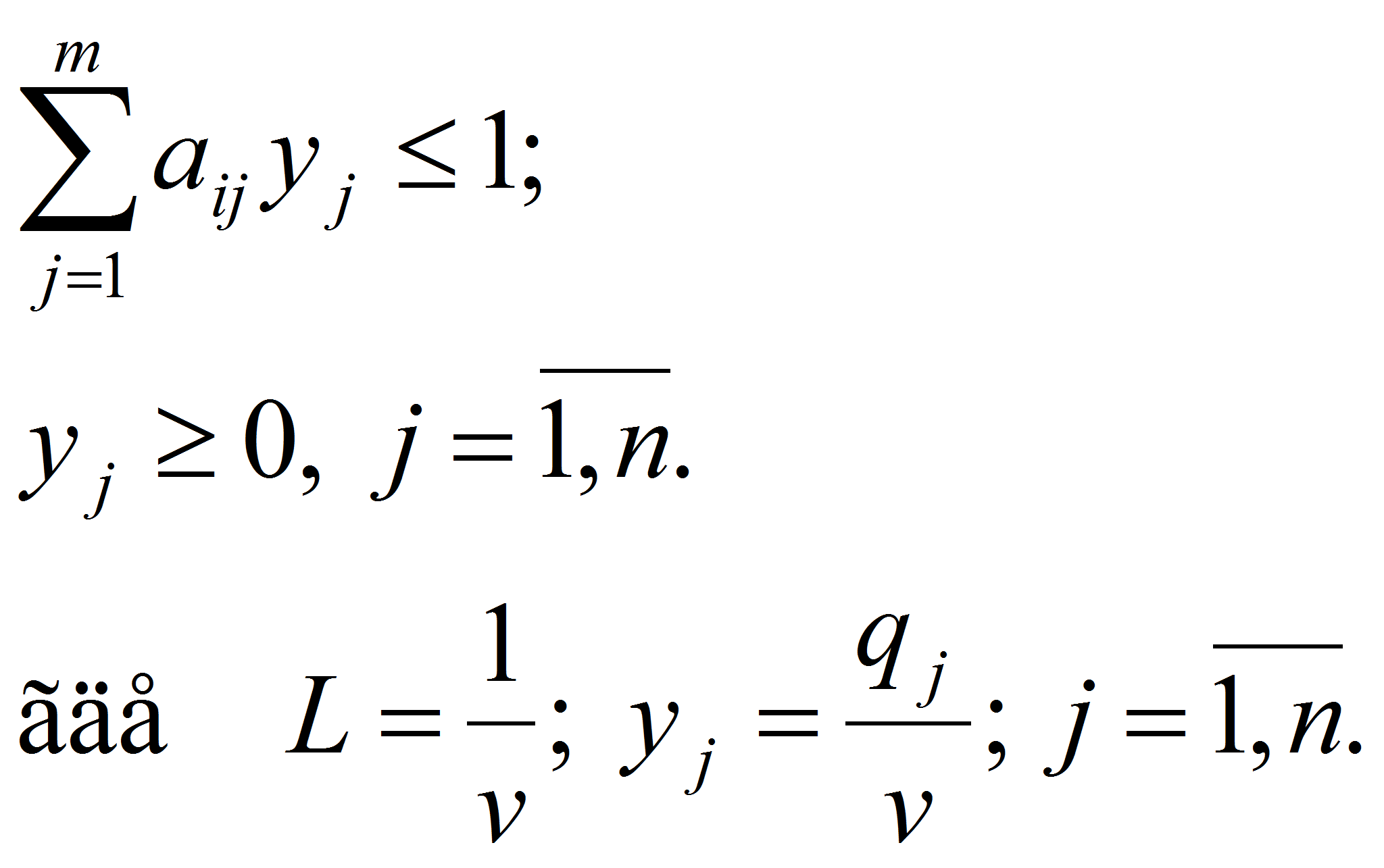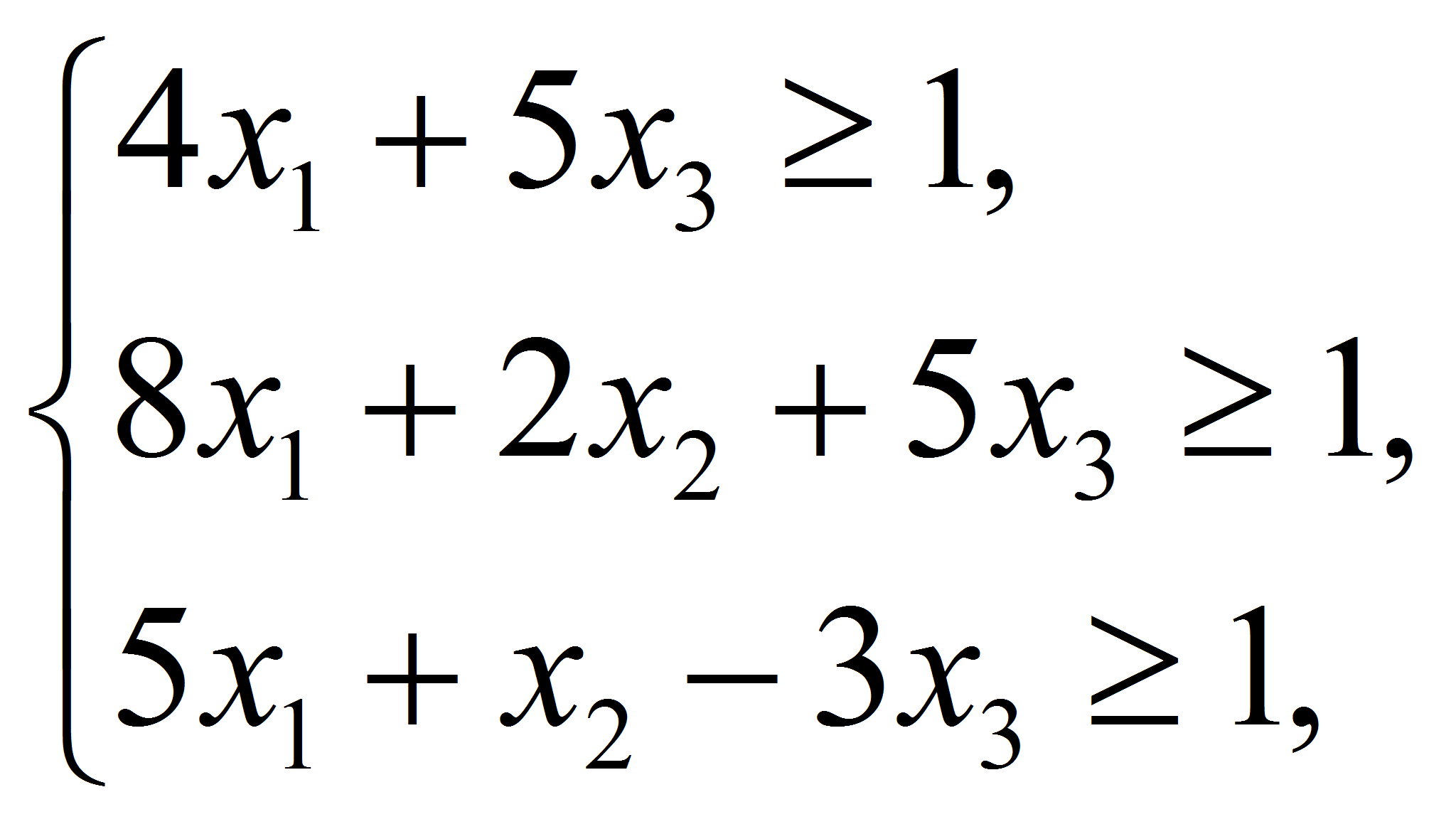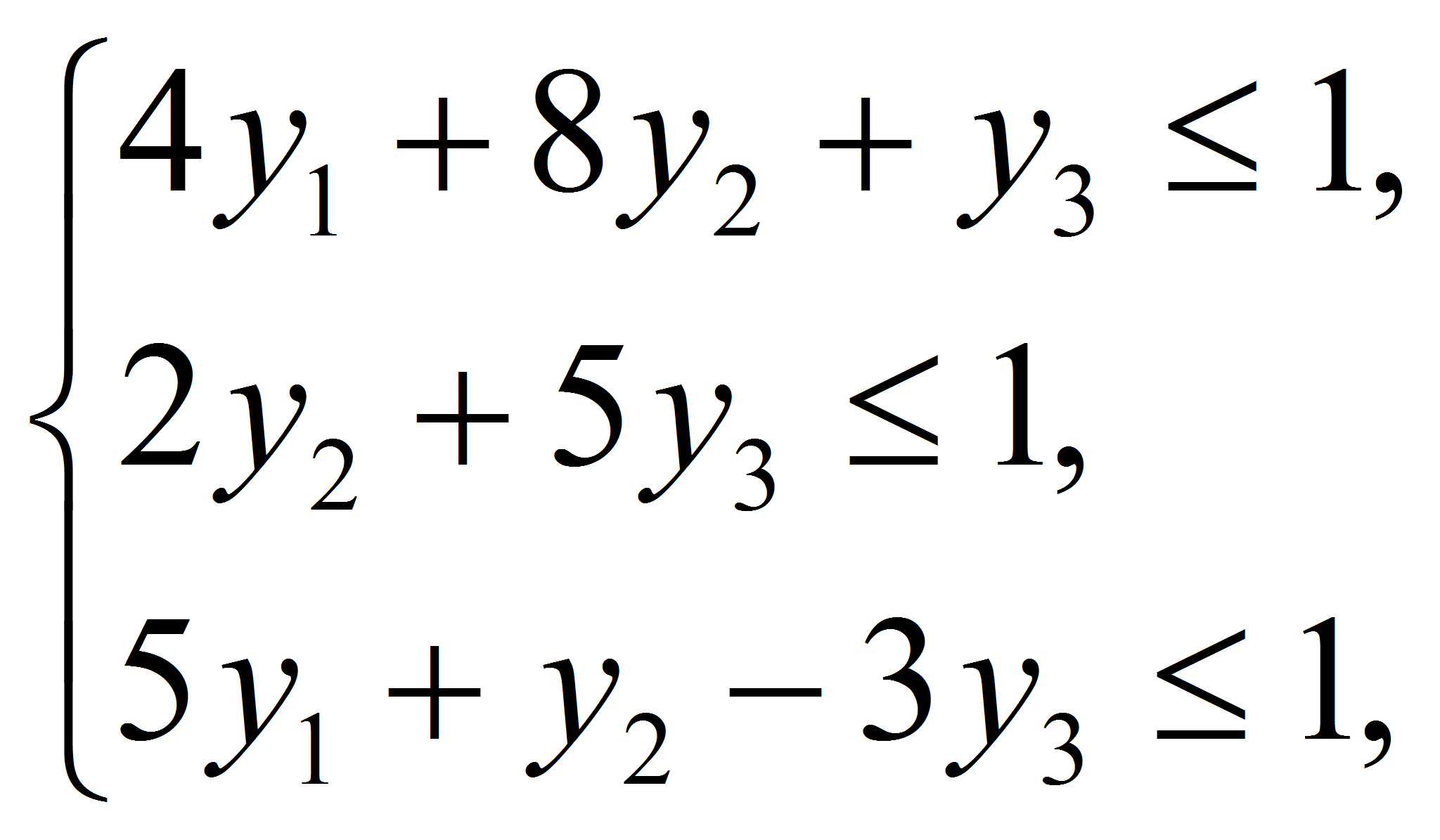Решение игровых задач с нулевой суммой с помощью Microsoft Excel
Автор: Захарова Татьяна Николаевна
Рубрика: 8. Педагогика профессиональной школы и среднего профессионального образования
Опубликовано в
международная научная конференция «Актуальные задачи педагогики» (Чита, декабрь 2011)
Статья просмотрена: 4426 раз
Библиографическое описание:
Захарова, Т. Н. Решение игровых задач с нулевой суммой с помощью Microsoft Excel / Т. Н. Захарова. — Текст : непосредственный // Актуальные задачи педагогики : материалы I Междунар. науч. конф. (г. Чита, декабрь 2011 г.). — Чита : Издательство Молодой ученый, 2011. — С. 176-181. — URL: https://moluch.ru/conf/ped/archive/20/1343/ (дата обращения: 18.04.2024).
Рассмотрим общий случай игровой задачи m x n с нулевой суммой, когда модель задачи не имеет седловой точки. Такую модель можно представить в виде матрицы (табл.1):
Таблица 1. Общая таблица стратегий
|
Стратегии |
В1 |
В2 |
… |
Вn |
|
A1 |
a11 |
a12 |
|
a1n |
|
A2 |
a21 |
a22 |
|
a2n |
|
…. |
|
|
|
|
|
Am |
am1 |
am2 |
|
amn |
Оптимальное
решение необходимо искать в области смешанных стратегий. Обозначим
вероятности применения стратегий первого игрока (игрока А) через
![]() ,
а цену игры — через v.
Оптимальная смешанная стратегия игрока А определяется из условия
,
а цену игры — через v.
Оптимальная смешанная стратегия игрока А определяется из условия
Пусть
Поскольку при оптимальной стратегии средний выигрыш не меньше v при любой стратегии противника, то справедлива система n неравенств:
Или
Тогда задача отыскания оптимальной смешанной стратегии игрока А может быть сформулирована в виде задачи линейного программирования.
Для этого необходимо максимизировать целевую функцию F =v при ограничениях
Введем новые неизвестные:
Разделим левую и правую части неравенств (1) и (2) на v, получим:
В силу того что
max v = min 1/v = min{x1+x2+…+xm}.
задача принимает вид
F= x1+x2+…+xm → min (4)
при ограничениях
Для второго игрока (игрока В) оптимальная стратегия определяется из условия:
при условии
q1+q2+…+qn = 1
Эта задача записывается как симметричная двойственная задача линейного программирования к задаче игрока A (4), (5):
L= y1 +y2+… +yn → max (6)
при ограничениях
Задачи игроков A и В решают симплекс-методом.
Использование возможностей Microsoft Excel позволяет существенно облегчить и ускорить решение этой задачи.
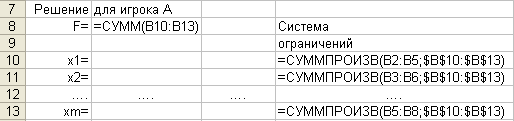
Сначала нужно создать исходную таблицу:
Затем, на основе этой таблицы записать формулы для нахождения решения:
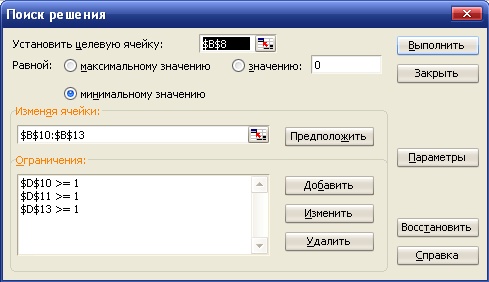
Для нахождения решения используется надстройка Поиск решения. Нужно выделить ячейку, в которой вычисляется значение функции F и вызвать надстройку Поиск решения. Заполнить окно поиска решения:
В поле Ограничения нужно задать формулы для всех ограничений. Затем нажать кнопку Параметры и отметить поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК, затем Выполнить.
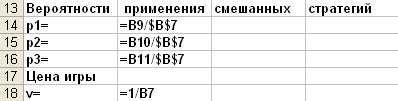
Чтобы найти значения вероятностей и цену игры нужно записать формулы:
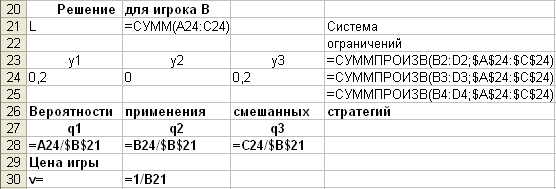
Решение задачи для игрока В выполняется по аналогичной схеме согласно формулам (6), (7).
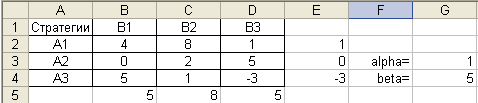
Рассмотрим пример
решения задачи. Найдем
решение игры, заданной матрицей
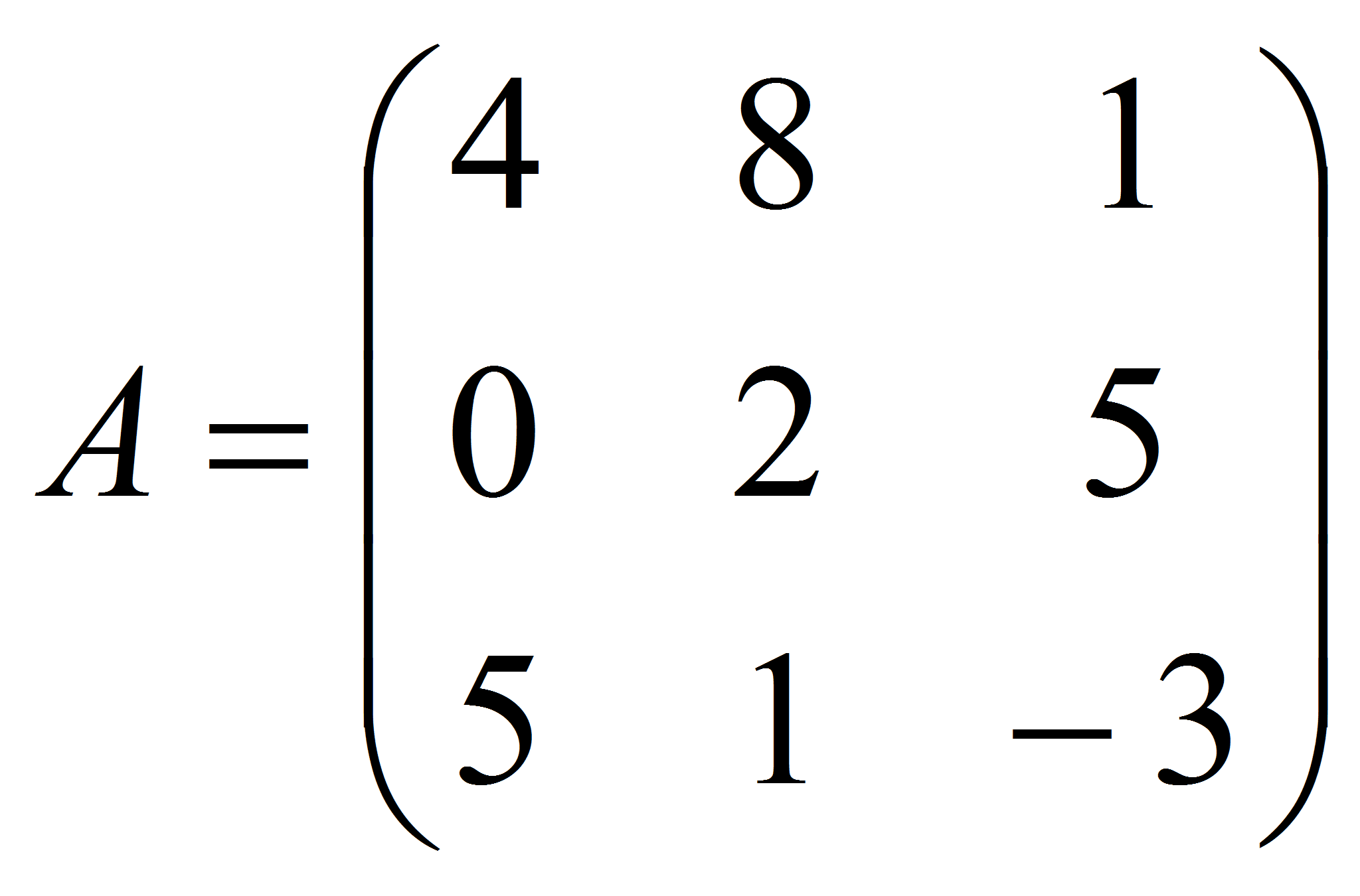 .
.
Проверим наличие седловой точки.
В режиме отображения формул эта запись имеет вид:
Поскольку нижняя цена игры (минимальный выигрыш игрока А) и верхняя цена игры (максимальный проигрыш игрока В) не равны, то модель данной задачи не имеет седловой точки. Поэтому решение следует искать в смешанных стратегиях. Составим задачи линейного программирования для нахождения решений игроков А (согласно формулам (4), (5)) и В(согласно формулам (6), (7)):
Для решения этих систем используем надстройку «Поиск решения». Сначала оформим задачу для поиска решения игрока А:
В режиме отображения формул:
Затем нужно активировать ячейку В7 и запустить надстройку Поиск решения. Далее заполнить окно Поиска решения:
Затем нажать кнопку Параметры и отметить поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК, затем Выполнить.
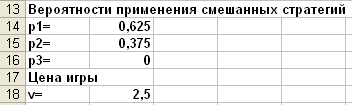
Получим результат:
Вероятности применения смешанных стратегий и цену игры найдем по формулам: pi=xi/F, v=1/F.
В режиме отображения формул:
Аналогично найдем решение для игрока В:
В режиме отображения формул:
Литература:
1. Акулич И.Л. Математическое программирование в примерах и задачах. М. «Высшая школа», 1993г.
2. Агальцов В.П., Волдайская И.В. Математические методы в программировании М. ИД «Форум» - ИНФРА-М, 2006г.
3. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем М. «Финансы и статистика», 2003г.
4. Партыка Т.Л., Попов И.И. Математические методы М. ИД «Форум» - ИНФРА-М, 2007г.
Похожие статьи
Создание и использование программы для статистического...
стратегия, игра, игрок, матричная игра, цена игры, решение игры, нулевая сумма, участник, верхняя цена игры, платежная матрица. Поиск решения как средство решения задач оптимизации...
Теория игр: основные понятия, типы игр, примеры
Для второго игрока самой оптимальной смешанной стратегией является стратегия . Запишем цену игры
Алгоритм. Иначе цена игры находится в промежутке и решение игры находится в смешанных стратегиях.
Поиск решения как средство решения задач оптимизации...
Получится запись как на рис.1. В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок Линейная модель и задать условия неотрицательности переменных, установив флажок
Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.
Математическое моделирование оптимальных стратегий...
‒ аспект оптимальных решений — теория математических моделей принятия оптимальных решений вусловиях конфликтов.
игрок, функция распределения, стратегия, конфликтная ситуация, функция, математическая модель, непрерывная игра, обычный риманов интеграл...
Интеграл Стильтьеса в теории игр | Статья в журнале...
Аналогичным образом с помощью интеграла Стильтьеса находится цена непрерывной игры и оптимальная смешанная стратегия для обоих игроков-стратегов. Предположим, что есть платежная функция (или функция выигрыша)...
Целочисленное решение задач линейного программирования...
Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Решение многокритериальных задач линейного...
Рис. 1. Оптимальное решение задачи.
Основные термины (генерируются автоматически): критерий, задача, учет уступок, полученное решение, поиск решения, матрица коэффициентов, важность критерия, допустимая уступка, линейное программирование.
Применение метода линейного программирования для решения...
Метод линейного программирования при решении текстовых задач графически имеет следующий алгоритм
Литература: 1. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели.
Линейное программирование | Статья в журнале «Молодой...»
Модель линейного программирования имела бы множество переменных решений
Решение задач оптимального раскроя средствами MS Excel. Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века.
Похожие статьи
Создание и использование программы для статистического...
стратегия, игра, игрок, матричная игра, цена игры, решение игры, нулевая сумма, участник, верхняя цена игры, платежная матрица. Поиск решения как средство решения задач оптимизации...
Теория игр: основные понятия, типы игр, примеры
Для второго игрока самой оптимальной смешанной стратегией является стратегия . Запишем цену игры
Алгоритм. Иначе цена игры находится в промежутке и решение игры находится в смешанных стратегиях.
Поиск решения как средство решения задач оптимизации...
Получится запись как на рис.1. В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок Линейная модель и задать условия неотрицательности переменных, установив флажок
Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.
Математическое моделирование оптимальных стратегий...
‒ аспект оптимальных решений — теория математических моделей принятия оптимальных решений вусловиях конфликтов.
игрок, функция распределения, стратегия, конфликтная ситуация, функция, математическая модель, непрерывная игра, обычный риманов интеграл...
Интеграл Стильтьеса в теории игр | Статья в журнале...
Аналогичным образом с помощью интеграла Стильтьеса находится цена непрерывной игры и оптимальная смешанная стратегия для обоих игроков-стратегов. Предположим, что есть платежная функция (или функция выигрыша)...
Целочисленное решение задач линейного программирования...
Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Решение многокритериальных задач линейного...
Рис. 1. Оптимальное решение задачи.
Основные термины (генерируются автоматически): критерий, задача, учет уступок, полученное решение, поиск решения, матрица коэффициентов, важность критерия, допустимая уступка, линейное программирование.
Применение метода линейного программирования для решения...
Метод линейного программирования при решении текстовых задач графически имеет следующий алгоритм
Литература: 1. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели.
Линейное программирование | Статья в журнале «Молодой...»
Модель линейного программирования имела бы множество переменных решений
Решение задач оптимального раскроя средствами MS Excel. Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века.