Межпредметные связи физики и математики при изучении вопросов геометрической оптики в школьном курсе физики

Abstract. This article is an analysis of the feasibility of MPS physics and mathematics in the study of problems of geometrical optics in school education

Keywords: interdisciplinary communication, physics, mathematics, geometrical optics solution.

Взаимосвязь между школьными дисциплинами имеет принципиальное педагогическое значение, она состоит в обеспечении многосторонних контактов между всеми дисциплинами с целью гармонического развития учащихся. Осуществление межпредметных связей (МПС) обеспечивает формирование единого представления школьников о явлениях природы, технических процессах и физических закономерностей, делает их знания более глубокими и практичными, что является неотъемлемой частью школьного образования в условиях компетентностного подхода.

В научно-методической литературе существует большое количество определений понятия «межпредметные связи», описываются различные подходы к их педагогической оценке и различные классификации. Проведенный анализ различных трактовок данного понятия, позволяет сделать вывод, что конечно они все верны, но их нельзя считать полными, поэтому необходимо подвести их под более полное и широкое понятие. На наш взгляд, если за основу данного понятия взять определение, которое приводит в своих работах Г.Ф. Федорец [4], получим, что межпредметные связи есть педагогическая категория для обозначения синтезирующих, интегративных отношений между объектами, явлениями и процессами реальной действительности, нашедших свое отражение в содержании, формах и методах учебно-воспитательного процесса и выполняющих образовательную, развивающую и воспитывающую функции в их единстве.

Анализ возможностей МПС в школьном образовании позволяет выделить у них четыре дидактические функции:

- методологическую;

- образовательную;

- развивающую;

- конструктивную.

Проанализировав основной состав учебных дисциплин основной и средней школы, начиная с седьмого класса, нами были определены возможности реализации МПС физики с ними (таблица 1).

Уровень возможности осуществления МПС физики

со школьными дисциплинами

(«++» - высокий уровень «возможности», «+» - средний уровень «возможности», «±» - низкий уровень «возможности», «–» - нет возможности)

Как видно из таблицы 1, большинство дисциплин позволяют на достаточно высоком уровне осуществлять МПС с физикой, однако первенство отдается четырем дисциплинам: биология, химия, астрономия и математика (алгебра и геометрия)[1] .

Математика как наука сформировалась намного раньше, чем физика, по мере развития физических знаний математические методы находили всё большее применение в физических исследованиях.

Математический аппарат необходим физике как язык для описания физических процессов и явлений, и является одним из методов физического исследования. Физика ставит перед человеком те ли иные задачи, при этом она побуждает создавать необходимые для их решения математические идеи и методы, которые в дальнейшем служат базой для развития математической теории.

Математика многое даёт физике. Так язык дифференциального и интегрального исчисления открывает большие возможности для более строгого определения ряда физических законов (второго закона Ньютона, закона электромагнитной индукции), формул, выражающих суть отдельных физических понятий (силы тока, возникающего в рамке, вращающейся в магнитном поле и др.). Идеи теории симметрии, тесно связанны с вопросами геометрией, что позволяет учащимся легче понять и усвоить общие научные положения строения кристаллов в молекулярной физике (10 класс); в оптике изучить построение изображений в зеркалах и линзах (8 и 11 классы).

Рассмотрим возможности МПС физики и математик на примере изучения вопросов геометрической оптики в 8 и 11 классах (таблица 2) [2,3].

Таблица 2

Элементы математических знаний при изучении

Анализ содержания вопросов геометрической оптики в школьных учебниках [2, 3], позволяет сделать вывод, что в 8 классе 56 % уроков по изучению данных вопросов позволяют реализовать МПС физики и математики, а в 11 классе – 67 %.

Покажем возможность применения МПС через интеграцию знаний математики в физику при решении задачи на закон преломления света.

Задача.

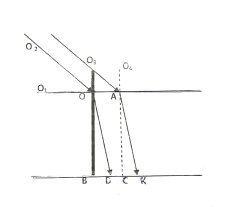
Шест высотой 3 м выступает из воды на 50 см. Определить длину тени от шеста на поверхности воды и на дне водоема, если угловая высота солнца над горизонтом 300 (показатель преломления воды 1,33).

Дано:

а = 3 м

в = 0,5 м

φ = 300

n = 1,33

Найти: L1, L2

Ответ: длина тени на поверхности воды 85 см, а на дне 2 м95 см.

В ходе преподавания физики и математики необходимо регулярно обращать внимание учащихся на то, что математика является мощным средством для обобщения физических понятий и законов. Во взаимоотношениях физики и математики большое место занимает пересечение внутренних потребностей с развитием наук. Такое пересечение обычно приводит к важным открытиям, как в математике, так и в физике. Математика представляет аппарат для выражения общих физических закономерностей и методы раскрытия новых физических явлений и фактов, а физика, в свою очередь, стимулирует развитие математики постановкой новых задач.

Литература

1. Журавлева, Н.С. Реализация межпредметных связей физики и биологии через решение физико-зоологических задач [Текст] / Н.С. Журавлева, Е.В. Ермакова // XXIII Ершовские чтения : Межвуз. сб. науч. ст. – Ишим, 2013. – С. 148-149.
2. Мякишев, Г.Я. Физика. 11 класс [Текст] : учеб. для общеобразоват. организаций: базовый и профильный. уровни / Г.Я. Мякишев, Б.Б. Буховцев, В.М. Чаругин; под ред. Н.А. Парфентьевой. – М.: Просвещение, 2014. – 399 с.
3. Перышкин, А.В. Физика. 8 класс [Текст]: учеб. /А.В. Перышкин. – М.: Дрофа : Вертикаль, 2013. – 240 с.
4. Федорец, Г.Ф. Межпредметные связи педагогики с психологией [Текст]: учеб. пособие к спецкурсу / Г. Ф. Федорец. – Л. : ЛГПИ им. А. И. Герцена, 1988. - 22 с.