Реакция синтезаторов на паразитное приращение фазы опорного колебания

 

Исследование реакции схем синтезаторов на паразитное приращение фазы опорного колебания необходимо по двум причинам. Во-первых, необходима проверка стабилизирующих свойств синтезаторов при включении в них цепи автокомпенсации частотных искажений, во-вторых, представляет интерес вопрос о том, каким образом использование цепи автокомпенсации влияет на паразитную фазовую модуляцию (ПФМ) синтезатора, являющуюся следствием действия дестабилизирующих факторов на опорное колебание.

Следует отметить, что в связи с тем, что цепь автокомпенсации используется только в первом кольце импульсно-фазовой автоподстройки частоты (ИФАПЧ1), исследование этой реакции можно провести только для первого кольца ИФАПЧ1, при этом сравнение реакции на паразитное приращение фазы опорного колебания следует провести для первого кольца ИФАПЧ1 схемы синтезатора с модуляцией по методу ЧМ1, а также для первого кольца ИФАПЧ1 схемы синтезатора с модуляцией по методу ЧМ1АК.

Для нахождения передаточных функций систем ИФАПЧ1 первой и второй схем преобразуем их к виду, когда паразитное приращение фазы опорного колебания проходит на выход генератора, управляемый напряжением(ГУН1) по прямому каналу, при этом в преобразованных структурных схемах не будем учитывать цепи полезной модуляции в силу линейности систем.

На рис. 1 изображена структурная схема ИФАПЧ1 первого синтезатора с модуляцией по методу ЧМ1, а на рис. 2 структурная схема ИФАПЧ1 второго синтезатора с модуляцией по методу ЧМ1АК, в которых паразитные приращения фазы опорного колебания проходят на выход ГУН1.

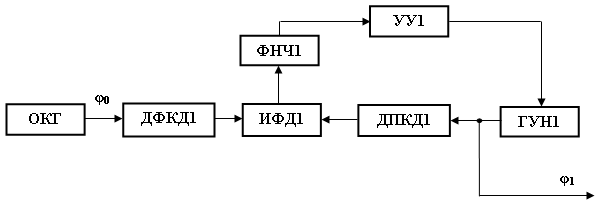
Рис. 1. Структурная схема ИФАПЧ1 синтезатора с модуляцией по методу ЧМ1, в котором ПФМ опорного колебания проходит на выход ГУН1

 

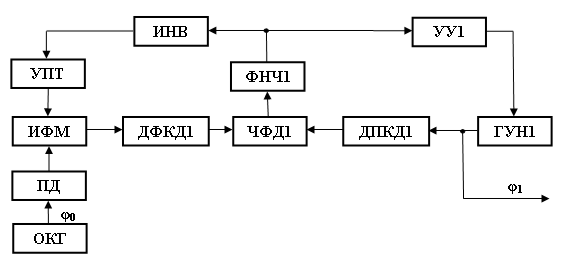
Рис. 2. Структурная схема ИФАПЧ1 синтезатора с модуляцией по методу ЧМ1АК, в котором ПФМ опорного колебания проходит на выход ГУН1

 

Для определения передаточных функций колец ИФАПЧ1, изображенных на рис. 1 и рис. 2, составим их эквивалентные операторные схемы, причем под передаточными функциями будем понимать отношение операторного изображения паразитной девиации фазы выходного колебания ∆φ1(р) ГУН1 к операторному изображению паразитной девиации фазы опорного колебания ∆φ0(р) при нулевых начальных условиях, т. е. при условии, что кольцо ИФАПЧ1 обоих синтезаторов находится в режиме синхронизма и отсутствует полезное модулирующее воздействие.

При составлении эквивалентных операторных схем примем коэффициент усиления УУ1 К1 = 1, а также примем, что коэффициент деления ПД Rп равен единице. С учетом этого эквивалентные операторные схемы колец ИФАПЧ1 синтезаторов с модуляцией по методу ЧМ1 и по методу ЧМ1АК, отражающие зависимость ∆φ1(р) от ∆φ0(р), будут иметь вид, изображенный, соответственно, на рис. 3 и рис. 4.

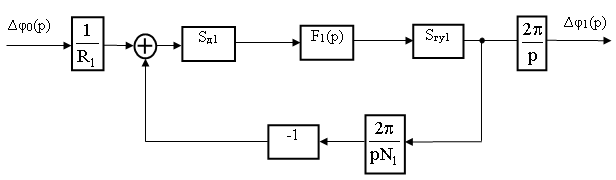
Рис. 3. Эквивалентная операторная схема кольца ИФАПЧ1 синтезатора с модуляцией по методу ЧМ1, отражающая зависимость ∆φ1(р) от ∆φ0(р)

 

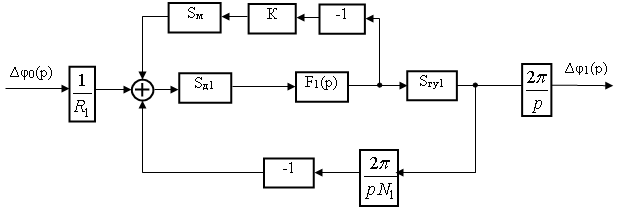
Рис. 4 Эквивалентная операторная схема кольца ИФАПЧ1 синтезатора с модуляцией по методу ЧМ1АК, отражающая зависимость ∆φ1(p) от ∆φ0(p)

 

В соответствии с рис. 3 нормированная на N1/R1 передаточная функция кольца ИФАПЧ1 первого синтезатора

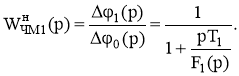(1)

При использовании в качестве ФНЧ1 интегрирующего фильтра выражение (1) можно переписать в виде:

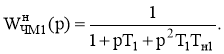(2)

Эквивалентную операторную схему, изображенную на рис. 4 с помощью метода преобразования эквивалентных схем можно преобразовать к виду, изображенному на рис. 5, на которой передаточная функция автокомпенсатора

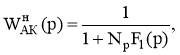(3)

где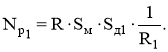

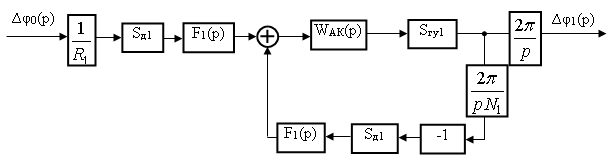
Рис. 5. Преобразованная эквивалентная операторная схема, изображенная на рис. 4

 

В этом случае нормированная на N1/R1 передаточная функция кольца ИФАПЧ1 второго синтезатора

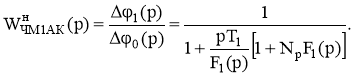(4)

При использовании в качестве ФНЧ1, как и в предыдущем случае, интегрирующего фильтра выражение (4) можно переписать в виде:

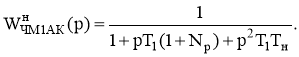(5)

Сравнивая (2) и (5), видно, что их характеристические уравнения совпадают, следовательно, обе эти системы устойчивы.

Кроме этого, из сравнения (5) с (2) видно, что для анализа частотных характеристик колец ИФАПЧ1 обоих синтезаторов можно пользоваться выражением (5), полагая, что для синтезатора с модуляцией по методу ЧМ1 Np = 0. В связи с этим в дальнейшем для сокращения записи введем для обоих синтезаторов обозначение передаточных функций первых колец ИФАПЧ1 Wн(р).

Для анализа амплитудно-частотных характеристик (АЧХ) колец ИФАПЧ1 обоих синтезаторов, которые характеризуют реакцию предложенных схем синтезаторов на паразитные приращения фазы опорного колебания заменим в (5) p на jΩ и получим комплексную частотную характеристику (КЧХ) колец ИФАПЧ1

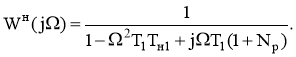(6)

Разделяя КЧХ (6) на действительную и мнимую составляющие и находя модуль (6), получим выражение для АЧХ колец ИФАПЧ1

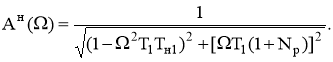(7)

Расчет АЧХ проведем с использованием программы MathCAD 7.0 по формуле

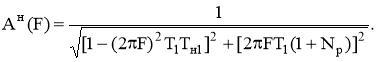(8)

На рис. 6 приведены АЧХ при Tн1 = 16∙103 с, а на рис. 7 — при Tн1 = 8∙10–3 с, при этом на обоих рисунках приведены графики, рассчитанные при T1 = 5∙10–3 с. Кроме того, на обоих рисунках сплошные линии соответствуют Np = 0, точечные — Np = 10, пунктирные — Np = 100.

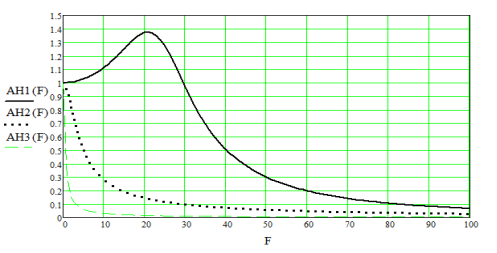
Рис. 6. АЧХ при Tн1 = 16∙103 с

 

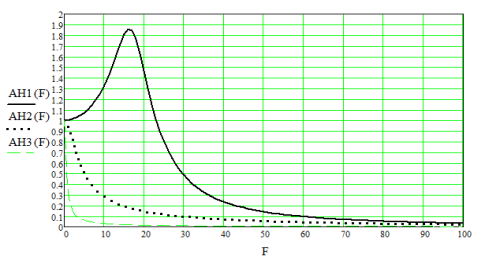
Рис. 7. АЧХ при Tн1 = 8∙10–3 с

 

Из сравнения графиков, приведенных на этих рисунках, видно, что введение дополнительной цепи автокомпенсации частотных искажений закона модуляции приводит к сужению полосы пропускания эквивалентного ФНЧ, каковым являются кольца ИФАПЧ1 обоих синтезаторов для паразитных отклонений фазы опорного колебания, являющихся следствием влияния различных дестабилизирующих факторов. Кроме того, анализ этих рисунков показывает, что при использовании цепи автокомпенсации полоса пропускания эквивалентного ФНЧ не зависит от полосы пропускания ФНЧ1 в цепи управления, а определяется только значением коэффициента регулировки Np. Это благоприятно сказывается на спектральной частоте выходного сигнала синтезатора, так как при этом уменьшается передаточная модуляционная функция.

Введение дополнительной цепи авторегулирования сужает полосу пропускания кольца ИФАПЧ1, что благоприятно сказывается на спектральных характеристиках выходного сигнала.

 

Литература:

 

1.                Андрющенко В. А. Теория систем автоматического управления / В. А. Андрющенко. — Л.: Изд-во ЛГУ, 1990.– 251 с.
2.                Анисимов С. Л. Тандемные цифровые синтезаторы частот с дробно-кратным делителем частоты второго кольца / С. Л. Анисимов // Всероссийская научно-практическая конференция «Актуальные вопросы эксплуатации систем охраны и защищенных телекоммуникационных систем»: сборник материалов. — Воронеж: Воронежский институт МВД России, 2007. — С. 8–9.
3.                Анисимов С. Л. Построение двухкольцевых частотно-модулированных синтезаторов частот на современной цифровой элементной базе / С. Л. Анисимов, П. А. Попов // Вестник Воронежского института МВД России. — 2007. — № 1. — С. 174–177.
4.                Артым Л. Д. Применение фазовой автоподстройки частоты / А. Д. Артым // Радиотехника. — 1958. — № 8. — С. 76–79.
5.                Артым Л. Д. Частотные методы анализа и синтеза систем ФАПЧ / Л. Д. Артым, С. В. Трифонов. — М.: Связь, 1976.– 160 с.
6.                А.с. 1707765 СССР, МКИ Н03L 7/16. Цифровой синтезатор частот с частотной модуляцией / И. П. Усачев, П. А. Попов (СССР) // Б.И.– 1992.– № 3.– 235 с.
7.                Белов Л. А. Синтезаторы частот и сигналов: учебное пособие / Л. А. Белов. — М.: САЙНС-ПРЕСС, 2002.– 80 с.
8.                Бесекерский В. А. Теория систем автоматического регулирования / В. А. Бесекерский, Е. П. Попов. — М.: Наука, 1972. — 767 с.
9.                Борисов В. И. Помехозащищенность систем радиосвязи. Вероятностно-временной подход / В. И. Борисов, В. М. Зинчук. — М.: Радио и связь, 1999. — 252 с.
10.            Борисов В. И. Помехозащищенность систем радиосвязи с расширением спектра сигналов модуляцией несущей псевдослучайной последовательностью / В. И. Борисов, В. М. Зинчук и др.– М.: Радио и связь,2003. — 640 с.