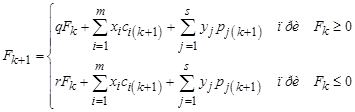В работе рассматривается задача формирования оптимального инвестиционного портфеля, состоящего из инвестиционных проектов, когда предусмотрены выплаты по группам проектов. Теория инвестиционных проектов изложена в [1, с.21]. Под (дискретным) инвестиционным проектом (потоком платежей) понимается вектор С = (c0 , c1 , … , cn), компонента ck которого это платеж (при ck<0) или возврат средств (при ck>0) в момент времени j. Предположим, что инвестору предложен набор проектов С1 , С2 , …, Сm, из которых необходимо выбрать несколько инвестиционных проектов для финансирования. Предполагается, что в качестве альтернативного используется вложение средств с годичным коэффициентом накопления q. Впервые задачи формирования оптимального портфеля из инвестиционных проектов были поставлены в работе [2, с.235], в работе [3, с.17] для их решения применены методы линейной оптимизации. В работе [4, с.48] рассматриваются оптимизационные задачи, где в качестве целевой функции принимается модифицированная рентабельность, при этом учитываются и другие характеристики проекта. В [5,с.230;6,с.800] поставлена и проанализирована задача формирования оптимального портфеля инвестиционных проектов, если для некоторых групп проектов предусмотрены групповые платежи. Например, необходим офис, если финансируется хотя бы один проект в некотором регионе. Другой пример связан с приобретением специального транспорта. В работах [5,с.230;6,с.800] предполагалось, что для групп проектов могут осуществляться только платежи. В то же время, в приведенных примерах офис или транспортное средство на некоторое время может сдаваться в аренду, а это приведет и к поступлениям средств.
ПОСТАНОВКА ЗАДАЧИ
Будем считать, что все проекты С1 , С2 , …, Сm сосредоточены на общем временном интервале [0,n], для этого при необходимости можно дополнить проекты нулевыми платежами. Предполагается, что проекты независимы [1, с.21], т.е. выбор проекта для включения в портфель не зависит от того, какие проекты уже включены в него. Пусть выделены некоторые подмножества UjÌ{1,…,m} (j =1,…,s) проектов, для каждого из которых определен вектор платежей Pj = (Pj0 , Pj1 , … , Pjn), реализуемый при финансировании хотя бы одного проекта из множества Uj . Множества Uj могут пересекаться. Известны также годичный коэффициент накопления по банковским вкладам в течение n лет (за год вклад возрастает в q раз) и ставка r>q, под которую инвестор при необходимости занимает средства, т.е. долг за год возрастает в r раз. Начальный капитал инвестора обозначим через F-1.
Требуется выбрать проекты для финансирования, обеспечивающие максимально возможный капитал по окончании реализации проектов (сравнение портфелей по NFV – накопленной стоимости).
Введем следующие обозначения.
· Fk – капитал инвестора (или долг, если эта величина отрицательная) в момент k после всех выплат;
· хi - булевская переменная, равная 1, если i проект включается в портфель и 0 в противном случае;
· уj - булевская переменная, равная 1, если в портфель включен хотя бы один проект из множества Uj и 0 в противном случае;
Имеют место следующие ограничения:
Fk – капитал инвестора (или долг, если эта величина отрицательная) в момент k после всех выплат;
хi - булевская переменная, равная 1, если i-ый проект включается в портфель и 0 в противном случае;
уj - булевская переменная, равная 1, если в портфель включается хотя бы один проект из множества Uj и 0 в противном случае.
Имеют место следующие ограничения:
|
yj ≥ xi при iÎUj |
(1) |
|
yj≤ |
(2) |
|
хi ≥ хk , |
(3) |
если для выполнения k-го проекта должен выполняться i -ый проект.
Неравенства (1) и (2) в совокупности означают, что уj=1 тогда и только тогда, когда xi=1 хотя бы для одного iÎUj.
Неравенство (3) означает, что из хk =1 следует, что хi =1.
Имеем: F0= F-1+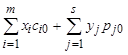 .Если F0 ≥ 0, то сумма на счете возрастает за год в q раз, с учетом платежей в момент времени 1 получим:
.Если F0 ≥ 0, то сумма на счете возрастает за год в q раз, с учетом платежей в момент времени 1 получим:
F1=qF0+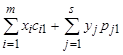 .
.
Если F0£0, то долг за год возрастет в r раз, откуда имеем
F1=rF0+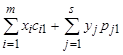 .
.
Если значение Fk (k=1,…,n-1) известно, то аналогично можно получить:
|
|
(4) |
Необходимо найти значения хi,уjÎ{0,1}, при которых величина NFV =Fn является максимальной.
Возможна ситуация, когда заимствование средств невозможно. В этом случае необходимо обеспечить неразорение инвестора в любой момент времени. Условие неразорения имеет вид
|
Fk³0 при k=0,1,…,n. |
(5) |
При выполнении условия (5) в условии (4) актуальна только верхняя строка.
Задача (1)-(5) является задачей булевского (нелинейного) программирования. Отметим, что она всегда допустима: значения хi=0, уj =0 удовлетворяют всем ограничениям.
Задача (1)- (4) сводится к задаче частично булевского линейного программирования, которая также всегда допустима. Для этого введем вспомогательные переменные Vi (i=0,…,n). Заметим, что поскольку r>q, из (4) следует равенство 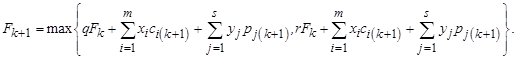
Задача принимает следующий вид:
Найти числа
х1,…, хmÎ{0,1}; y1,…,ysÎ{0,1}; F1,…,FnÎR
такие, что
yj³xi при iÎUj; yj≤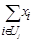 при iÎUj хi ≥ хk для зависимых проектов;
при iÎUj хi ≥ хk для зависимых проектов;
F k+1£qFk при k=0,1,…,n-1; Fk+1£rFk при k=0,1,…,n-1;
Fn ® max.
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
1. Для решения задачи (1)- (4) применялись метод ветвей и границ и метод отсечений (Гомори) [7,с.36;8,с.85]. Эти методы дают точное решение, но при этом являются трудоемкими. Вычислительный эксперимент показал, что при малом временном горизонте (до 5) применение метода Гомори для получения точного решения менее эффективно по сравнению с методом ветвей и границ, при временных горизонтах 8-9 наоборот.
2. Применялась эволюционная стратегия [9,с.57;10,с,182] простейшего вида ((1+1) –ЕА) по классификации работы [10, с.182]).
Для ее описания используем следующие термины.
· Особь (индивидуум) – инвестиционный портфель.
· Хромосома – приоритетный список проектов .
· Популяция – в данном алгоритме состоит из одной особи.
· Воспроизведение (оператор репродукции) – репродукция особи, т.е. формирование портфеля на основе текущего приоритетного списка.
· Отбор (оператор селекции). Применяется так называемый элитный отбор, то есть из всех особей отбираются особи с наибольшим возможным капиталом на конец временного горизонта.
· Оператор мутации. Проекты в приоритетном списке меняются местами случайным образом. В результате получается новая хромосома.
Проекты ранжируются по NPV (чистой приведенной стоимости) – первоначальная хромосома. На основе приоритетного списка формируется портфель (популяция), лучший портфель сохраняется (оператор селекции). Если далее улучшения не происходит список П перетасовывается случайным образом(мутация) и опять формируется популяция. Алгоритм заканчивает свою работу, если лучший портфель не улучшается заданное число раз.
ЗАКЛЮЧЕНИЕ
Для анализа эффективности описанных алгоритмов был проведен численный эксперимент. Анализ полученных результатов позволяет сделать следующие выводы:
- трудоемкость вычислений слабо зависит от длительности проектов, но существенно зависит от числа проектов;
- при малом временном горизонте (до 5) применение метода Гомори для получения точного решения более эффективно по сравнению с методом ветвей и границ, при временных горизонтах порядка 8-9 наоборот;
- эволюционная стратегия показала хорошие результаты в соотношении время работы/точность.
Работа выполнена при поддержке РФФИ (проект 07-06-00021).
Литература:
4. Бронштейн Е.М. (2004): Оптимальные инвестиционные портфели // Системное моделирование социально – экономических процессов. М.: ЦЭМИ РАН.
5. Balinski M.L. (1970): On a Selection Problem // Management Science. v.17. №11.
7. Корбут А.А., Сигал И.Х., Финкельштейн Ю.Ю., Об эффективности комбинаторных методов в дискретном программировании. М.: Наука,1979.
8. Сигал И.Х., Иванова А.П., Введение в прикладное дискретное программирование. М.:Физматлит, 2007.
9. Батищев Д.Ю. Генетические алгоритмы решения экстремальных задач // учебное пособие под ред. Я.Е.Львовича. Воронеж: Воронежский гос. техн. ун-т; Нижегородский ун-т. 1995.
10. Борисовский П.А., Еремеев А.В. О сравнении некоторых эволюционных алгоритмов // Автоматика и телемеханика, №2, 2004.