Ключевые слова: лента, фигура, петля, Мебиус.
В науке есть множество явлений, которые добавляют в нашу обыденность тайну и загадку. Одна из них — Лента Мебиуса. Все ее свойства достаточно подробно описаны в современной математике. Но люди, далекие от геометрических премудростей, не могут ее охарактеризовать, хотя они практически ежедневно сталкиваются с предметами, изготовленными по ее образу и подобию. [3]
Лента, петля, поверхность, лист и даже кольцо Мебиуса — эта математическая фигура имеет разные названия. Невероятно, но у нее всего одна поверхность и один край. Чтобы понять, о чем идет речь, и как такое возможно, соорудим ее сами. Это очень просто: из листа бумаги вырезать полоску прямоугольной формы, и, соединяя концы, перекрутить их на 180 градусов, как показано на рисунке 1.
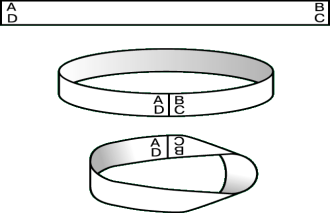
Рис. 1. Создание Ленты Мебиуса
А теперь попробуем закрасить полоску с одной стороны. В конечном итоге мы вернемся к начальной позиции. Проиллюстрируем это на рис. 2.


Рис. 2. Эксперимент с закрашиванием Ленты Мебиуса
Причем вся лента окажется целиком закрашенной. Это подтверждает наличие у фигуры всего одной стороны. Чтобы проверить то, что у Петли Мебиуса всего один край, проведем пальцем по одной из ее граней. И снова, как и в случае с раскрашиванием, окажемся в точке, с которой начали движение.
Лента Мебиуса — один из предметов изучения такой науки, как топология. В этом разделе математики исследуются «неизменные свойства объекта при его непрерывной деформации — растяжении, сжатии, изгибе, без нарушения целостности». [4]
Самое распространенное подобие Ленты Мебиуса — символ бесконечности, напоминающий перевернутую восьмерку. Научное название — лемниската, что с древнегреческого означает лента.
Этот необычный объект открыл немецкий математик Август Фердинанд Мебиус в 1858 году. Этому предшествовал случай — служанка, работавшая в его доме, сшила тканевую ленту в кольцо, перевернув по невнимательности один из ее концов. Вместо того чтобы отругать незадачливую девушку, Мёбиус произнес: «Ай да, Марта! Девочка не так уж глупа. Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!». В том же году другой талантливый математик Иоганн Листинг дошел до причудливой фигуры. Он дал название науке, изучающей непрерывность — топология, и написал целую серию основополагающих трудов. [5]
Но есть археологические находки, которые подтверждают, что о ленте было известно еще в древнем мире. Во Франции в музее города Арль находится древнеримская мозаика. На ней — Орфей, очаровывающий зверей игрой на арфе. В комплексе неоднократно изображен орнамент с перекрученной лентой.
Также отголоски ленты Мебиуса можно увидеть в одной старой задачке, называемой «Парадокс лгуна».
«Критянин Эпименид сказал: «Все критяне лжецы». Но Эпименид сам критянин. Следовательно, он лжец. Если Эпименид лгун, тогда его заявление, что все критяне лгуны — ложно. Значит, критяне не лгуны. Между тем Эпименид, как определено условием, — критянин, следовательно, он не лгун, и поэтому его утверждение «все критяне лгуны» — истинно».
Таким образом, мы пришли к взаимоисключающим предложениям. Одно из них утверждает, что высказывание «все критяне лгуны», является ложным, а другое, наоборот, на то, что высказывание истинное. Притом как в одном, так и в другом случае наши рассуждения логически строги, в них нет ни намеренных, ни непреднамеренных ошибок. Где же истина?
Было приложено немало усилий, чтобы объяснить этот странный результат. Имеется, например, такое решение.
Почему мы должны считать, что Эпименид говорит одну только ложь и никогда не говорит правды? Точно так же тот, кто считается правдивым, разве всегда утверждает лишь правду? В практике общения ложное обычно перемешано с истиной, и мы не найдем такого отпетого лгуна, который только бы лгал. Его легко изобличить, и тогда понимай все, что им сказано, наоборот.
В действительности, однако, положение гораздо сложнее. Парадоксу посвящена обширная литература. Он на самом деле вызывает недоумение. Легенда утверждает даже, что древнегреческий философ Кронос, испытав неудачу в попытках решить этот парадокс, от огорчения умер. С тех пор внимание к парадоксу лжеца не затухало. [3]
Интересные опыты можно провести с лентой. Разрежем фигуру вдоль по всей длине ровно посередине, как показано на рисунке 3.


Рис. 3. Эксперимент с разрезанием Ленты Мебиуса.
Вопреки ожиданию мы получим не два отрезка ленты и даже не два отдельных бумажных круга, а другую, еще более длинную ленту. Но в этом случае она будет перекручена не на 180, а на 360 градусов.
Со следующей петлей Мебиуса проведем другой эксперимент: отмерим 1/3 ширины ленты и отрежем по этой линии. В результате получим две отдельные ленты разных размеров, соединенные вместе, как в цепочке. При этом меньшая лента представляет собой 1/3 от начальной ширины ленты, длина L и поворот на 180 градусов. У более длинной ленты — тоже ширина 1/3 от начальной, но длина 2L. А поворот — на 360 градусов. Можно и дальше продолжить эксперимент, разрезая получившиеся ленты на еще более узкие.
Но Лента Мебиуса — это не какая-нибудь абстрактная фигура, которая используется только для математических целей. Она нашла широкое применение в жизни. На ее принципе функционируют транспортная лента в аэропорту, передаточные ремни на различных станках, пленка для записи в принтерах. Все потому, что благодаря такой конструкции лента равномерно изнашивается и дольше служит.
С тех пор, как была открыта петля Мебиуса, по всему миру на ее основе в различных отраслях ученые запатентовали свои изобретения. Например, Н. Тесле применение намотки катушек генератора по способу петли Мебиуса позволило улучшить свойства магнитных сердечников и добыть многофазную систему переменного тока. Американский ученый Ричард Дэвис сконструировал нереактивный резистор Мебиуса, способный гасить сопротивление, не вызывая электромагнитных помех.
Сегодня, в какой только сфере не используется эта удивительная фигура. Фокусники на ее основе строят многие свои фокусы. Архитекторы, дизайнеры интерьеров, литераторы и даже Кутюрье моды вдохновляются при создании шедевров. Спортсмены ввели одноименную фигуру высшего лыжного пилотажа. Самой известной работой, посвященной ленте Мебиуса считается картина Moebius Strip II, Red Ants или «Красные Муравьи» голландского художника-графика Маурица Эшера. На ней представлены муравьи, карабкающиеся по петле Мебиуса с обеих сторон. Но на самом деле сторона всего одна: муравьи ползут по бесконечной петле друг за другом по одной и той же поверхности.
Умы многих ученых волновала схожесть формы молекулы ДНК и петли Мебиуса. Советский цитолог Навашин выдвинул гипотезу, что форма кольцевой хромосомы по строению аналогична ленте Мебиуса. На эту мысль его натолкнул то, что «кольцевая хромосома, размножаясь, превращается в более длинное кольцо, чем в самом начале, или в два небольших кольца, но как в цепи продетых одно в другое» [2], что очень напоминает выше описанные опыты с листом Мебиуса.
В 2015 году группа физиков из Европы и США смогла закрутить свет в кольцо Мёбиуса. Для этого они использовали оптические линзы, и структурированный свет — «сфокусированный лазерный луч с преопределенными интенсивностью и поляризацией в каждой точке своего движения». [6] В итоге были получены световые ленты Мебиуса.
Существует еще одна масштабная теория: Вселенная — это огромная петля Мебиуса. Ее высказывал еще Эйнштейн. Он предположил, что «Вселенная замкнута, и космический корабль, стартовавший из определенной ее точки и летящий все время прямо, возвратится в ту же самую точку в пространстве и времени, с которой и началось его движение». [1]
Пока это всего лишь предположения. У них есть и сторонники, и противники. Никому неизвестно, к какому открытию подведет ученых, такой мистический объект, как Лента Мебиуса.
Литература:
1. Гусев В. А., Орлов А. И., Розенталь А. Л. «Внеклассная работа по математике», М.: Просвещение, 2006.
2. Данилова Ю. А. «Математический цветник» М.: Просвещение, 2009.
3. Стройк Д. Я. «Краткий очерк истории математики», М.: Просвещение, 2001.
4. Шарыгин И. Н. «Наглядная геометрия», М.: Дрофа, 2011.
5. http://www.frei.ru/golos/books/
6. http://www.kvant.info/

