Одной из важнейших областей применений математики является криптография — наука о шифрах, т. е. способах преобразования информации, позволяющих скрывать её содержание от посторонних.
Защита данных с помощью шифрования — одно из возможных решений проблемы конфиденциальности информации. Зашифрованные сообщения становятся открытыми и доступными только тем, у кого есть ключ.
Криптография — наука о методах обеспечения конфиденциальности, целостности и аутентификации информации.
Под конфиденциальностью здесь понимается невозможность прочтения информации несанкционированными людьми, целостность данных подразумевает невозможность внесения в них незаметных изменений, а аутентификация означает проверку подлинности авторства и свойств данных.
Шифрование — это процесс преобразования открытого текста в шифрованный с помощью определенного алгоритма, правил и ключа.
Математические методы и вычисления неразрывно связаны с криптографическими методами, которые мы и рассмотрим:
- Арифметика остатков или вычетов, используемая в шифровании и дешифровке методом простой постановки и многоалфавитной замены.
Предположим, что в русском алфавите буквы Е и Ё один элемент, так же как и буквы Ь и Ъ, если сюда прибавить символ пробела, то получится 32 символа. 0 — пробел, А — 1,.. Я — 31. Шифрование будет производиться по следующему алгоритму (например, для кодировки слова ЗИМА при помощи ключа Б):
− Берем порядковый номер первой буквы З — 8 и складываем с порядковым номером буквы ключа Б-2, получаем 10 — порядковый номер буквы Й;
− По порядку определяем другие буквы: К, О, В, получаем ЙКОВ;
− Для расшифровки используем вычитание. Если результат при сложении получился больше 31, то из него нужно вычесть 32 и использовать соответствующий символ.
2. При расшифровке без ключа может использоваться математический метод частотного анализа символов. Не секрет, что в разных алфавитах частота встречаемости разных букв разная. Например, в русском языке, наиболее встречаемая буква — «О». В таблице 1 представлены частоты встречаемости символов для русского алфавита:
Таблица 1
Частоты встречаемости символов русского алфавита в текстах
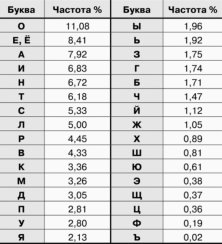
Так что для взлома достаточно большого текста, зашифрованного методом простой перестановки можно посчитать, насколько часто встречается та или иная буква в тексте и сравнить полученные частоты с данными, приведенными в таблице.
3. Стенография или метод Френсиса Бэкона. Шифрование производится битами, где все буквы русского алфавита можно закодировать двоичной системой от 00000 до 11111
Таблица 2
Кодировка букв русского алфавита в двоичной системе
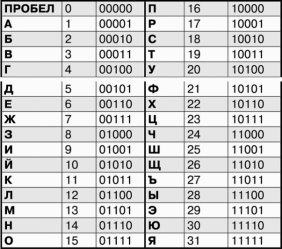
Если текст написан обычными буквами и буквами, выделенными жирным шрифтом, то нужно все сообщение разбить на группы по 5 символов, в которых обычные буквы будут иметь значение 0, остальные — 1.
Также могут использоваться заглавные и строчные буквы, буквы 2 цветов и т. д.
4. Операция XOR (исключающее ИЛИ) используется, когда текст, зашифрованный в двоичной системе, дополнительно шифруется с помощью одноалфавитной или многоалфавитной замены.
Основные правила исключающего ИЛИ приведены ниже:
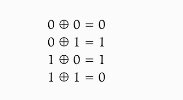
Эту операцию можно применять к двоичным числам. При этом она выполняется в столбик над каждым битом числа. Например:

Если сложить с помощью этого метода два двоичных числа, например X и Y, то получим число Z. Криптографическая привлекательность данной операции заключается в том, что Z+Y=X и Z+X=Y.
То есть расшифровка и зашифровка производится сложением. Это важное свойство обратимости результата постоянно используется криптографами.
В процессе изучения криптографии всегда хочется создать свой неповторимый шифр и пользоваться им с друзьями. Мне стало интересно, насколько мои одноклассники, и другие ученики нашей гимназии знакомы с шифрованием и его методами.
Для изучения этой информации была разработана анкета, состоящая из 5 вопросов:
− Как Вы считаете, необходимо ли защищать информацию?
− Какие способы защиты информации Вы знаете?
− Пользовались ли Вы когда-либо шифрами в письме или речи?
− Какие методы шифрования Вам знакомы?
− Создавали ли Вы когда-нибудь собственный шифр?
В опросе приняло участие 187 учеников 5–11 классов БОУ г. Омска «Гимназия № 115».
Анализ полученных данных показал, что 98,4 % опрошенных осознают, что информацию необходимо защищать. Знакомство с методами защиты информации неравномерно. Данные распределились следующим образом:
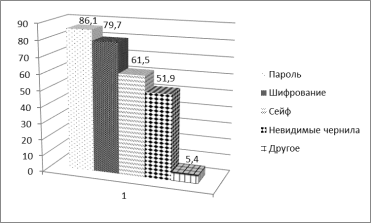
Рис. 1. Распределение ответов на вопрос: «Какие способы защиты информации Вы знаете?», в % к общему количеству опрошенных
Таким образом, можно утверждать, что самым известным способом защиты информации является установка паролей.
Около 67 % всех опрошенных пользовались шифрами в письме или речи.
Знакомство гимназистов с этими методами шифрования представлено на рисунке 2.
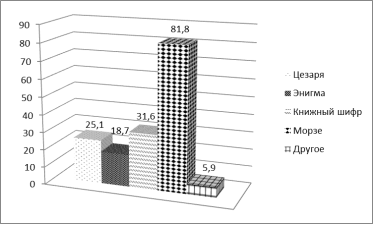
Рис 2. Распределение ответов на вопрос анкеты: «Какие методы шифрования Вам знаком?», в % к общему количеству опрошенных
Исходя из данных диаграммы, можно заключить, что 81,8 % анкетируемых знакома азбука Морзе, лишь 18,7 % учеников слышали об Энигме и только около 6 % смогли назвать другие методы шифрования, среди них: шифр Виженера, массонский шифр, атбаш, авторские тайные языки, двоичные коды, пляшущие человечки, шифры простой и многоалфавитной подстановки.
Чуть более 65 % респондентов создавали собственный шифр и пользовались им, что показывает заинтересованность гимназистов данным вопросом.
После проведения опроса было принято решение организовать криптографический квест среди старших школьников БОУ г. Омска «Гимназия 115» и БОУ г. Омска СОШ 141.
Основной целью проведения криптографического квеста является демонстрация возможностей шифрования и дешифровки для старших школьников (5–11 классы).
Проведение криптоквеста осуществляется по следующим основным этапам:
- Согласование с администрацией образовательного учреждения.
- Информирование потенциальных участников о мероприятии.
- Разработка шифров.
- Размещение первого шифра в группе социальной сети ВКонтакте в первый день мероприятия в 12:00 по местному времени.
- Выявление и награждение победителя.
Каждый желающий может попробовать взломать шифр, прислать администратору кодовое слово и получить в личной переписке шифр следующего этапа. То есть шифры 2–4 этапов открыто не выкладываются.
Ученики старшей школы взламывают сообщения вне школы, уделяя данному мероприятию столько времени, сколько считают нужным.
Первый ученик, разместивший ключевое сообщение на стене группы ВК становится победителем квеста.
Криптоквест включает 4 зашифрованных сообщения. Например, в БОУ г. Омска «Гимназия 115» один из шифров был на английском языке и зашифрован с помощью решетки Кардано, 2 сообщения зашифрованы методом подстановки и одно методом Бэкона.
Участников квеста, приславших первое ключевое слово в Гимназии № 115–15. С заданием 2 тура справилось 9 учеников, 3 тур прошли 6 человек. Победителем криптоквеста стала ученица 5Г класса Будко Вероника.
Участников группы, приславших первое ключевое слово для школы 141–22. Второй тур криптоквеста прошло 12 человек, 3 тур — 5 учеников, победителем стал ученик 8В класса Юнусов Михаил.
Как показали результаты, прием кодовых слов происходил и после определения победителя, что указывает на наличие интереса и азарта со стороны учеников.
Реализация криптографических квестов показала, что дети старшего школьного возраста активно интересуются методами шифрования, сталкивались с ними, умеют применять математические методы для их взлома.
Литература:
- Анин, Б. Ю. Англичане. Истоки. Шифртелеграмма Циммермана. // Радиоэлектронный шпионаж. — М.: Центрполиграф, 2017. — С. 323–327.
- Дориченко С. А., Ященко В. В. 1.4 Криптография как искусство. Немного истории. // 25 этюдов о шифрах: Популярно о современной криптографии. — М.: Теис, 1994. — С. 14–18.
- Душкин, Р. Шифры и квесты: таинственные истории в логических загадках. — м.: Издательство АСТ, 2017–288с.
- Жельников В. Становление науки криптологии // Кpиптография от папируса до компьютера. — М.: ABF, 1996. — 335 с.
- Скляров Д. В. 5.2 Криптография и наука // Искусство защиты и взлома информации. — СПб.: БХВ-Петербург, 2004. — 288 с.
- Скляров Д. В.. 6.2 Литература по криптологии // Искусство защиты и взлома информации. — СПб.: БХВ-Петербург, 2004. — 212 с.
- Токарева Н. Н. Об истории криптографии в России (рус.) // ПДМ. — 2016. — Декабрь. — С. 82–107.

