Piecewise-Quadratic Harmut’s Bases Functions and Factors Calculation Algorithm



Вработе исследуется известная система ортогональных кусочно-постоянных основных функций Хармута. В результате исследований, как слабая сходимость приближений, разрыва и другие выявлены. Разработано новый базис кусочно-квадратичной функции Хармута и предложен алгоритм быстрого спектрального преобразования в этом базисе.

In work the known system of orthogonal piecewise-constant Harmut’s basic functions is investigated. As a result of research their such lacks, as weak convergence of approximation, discontinuity and others are revealed. For their elimination the new basis of piecewise-quadratic Harmut’s functions is offered and the algorithm of fast spectral transformation in this basis is developed.

Keywords: signal, basis, spline, spectrum, fast transformations

For construction of models of the signals received from real objects, traditional harmonious functions are widely applied. It speaks that many signals received from real objects can be easily presented by set of harmonious fluctuations for what the device of Fourier analysis is used. Result of it is transition from time to frequency functions. However, representation of time function by harmonious functions is only one of many representations. Any full system of orthogonal functions can be applied to decomposition in series which correspond to Fourier series. As a result of research of methods of approach of functional dependences by piecewise -constant bases their such lacks, as weak convergence, discontinuity, rather low accuracy of approximation, necessity of great volume of memory for factors are revealed. For elimination of these lacks necessity of transition to piecewise -quadratic bases is shown. Advantages piecewise -quadratic bases: greater accuracy and good smoothness of approximation in comparison with piecewise-constant and piecewise-linear bases. These advantages allow to realize high-efficiency structures of the specialized processors differing also by high accuracy of approximation on the basis piecewise-quadratic bases. Lack of piecewise-quadratic bases — absence of fast algorithms of calculation of factors.

Helmut’s basic functions and parabolic basic splines. Wide distributions to technical appendices have received orthogonal systems the explosive basic functions set on the valid axis for which also there are algorithms of fast transformations. They can be broken into two classes:

1) global basic functions — such which value are not equal to zero on one subinterval. Walsh functions concern to this class [1, 5], numerical [2, 4], ramp function [1,5];

2) local basic functions, which nonzero values are set on the enclosed pieces. Examples are Haar’s functions [1, 2] and Harmut’s functions [3].

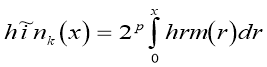(1)

In many practical appendices connected with restoration of functions between readout, continuous piecewise — linear bases it is not enough opportunities. It speaks, basically for two reasons:

1) because of low speed of convergence, caused by an estimation of an error piecewise — linear interpolation [3, 4, 5]:

, (2)

that often leads to significant expenses on factors;

2) because of not smooth nesses of approximation (the first derivative of basis functions is discontinuous) — is absent concept of curvature that causes essential restrictions. For example, it is possible to pass maxima and minima of functions. Construction of piecewise-quadratic basis can be executed by means of double integration piecewise- constant orthogonal Harmut’s functions:

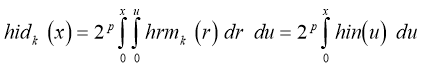(3)

With the purpose of inclusion of this basis in space we shall exclude linear components at those functions where they are available and результирующую system we shall designate {hidk (x)}. It consists of even and odd functions concerning the middle dyadic ally rational pieces, and these functions accept values «zero» on the ends of pieces. Graphically piecewise — quadratic Harmut’s functions {hidk (x)} are resulted on fig.1. c.

The wide popularity of methods a spline-approximating is explained to that they are the universal instrument of simulation of functions and in comparison with other mathematical methods with them information and hardware expenditures ensure the large exactitude of evaluations.

In the whole development of the theory of splines goes on two directions:

- Interpolation splines of defined boundary conditions, obeying to a system, and conditions in interior points of areas.

- Smoothing splines, when the problems of optimization of a different sort of functions are considered.

Spline methods are most effective in case of the discrete representation of input data’s. On an interval [a,b] we shall consider a grid :

: a = x0 < x1 <...< xn = b

Polinomial spline of an arbitrary degree m of an imperfection d (d-integer, 1 d  m) by nodes on a grid  is defined as the function ,

1) 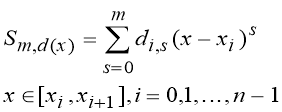(4)

2)

Derivative from a spline about (m — d +1) can be explosive on [a, b].

Their Fourier transform as finite function is determined by the formula:

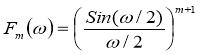
They also can be defined as outcomes of the operation of convolution of B-splines of the lowest degrees:

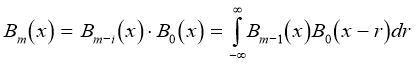
One of important properties of B-splines is the continuity its several derivative. Parabolic B-splines and their derivative of the first and second order are resulted.

For providing approximation on all interval [a, b] the B-splines should be given on wider area by means of introduction 2m, of additional nodes i=-m, m+1, n+m and, all nodes can be located nonuniformly.

Parabolic B-splines can be defined

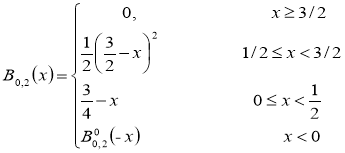(5)

Junction of the theory of basic splines and the Harmut’s spectral methods create a basis for development new algorithm of calculation of factors in piecewise-quadratic Harmut’s bases.

Conclusion. As a result of research on methods of approximating functional dependence shows their limitation as weak convergence, discontinuity, rather low accuracy of approximation, necessity of great volume of memory for factors are revealed. In order to overcome these limitations, the necessity for transition to piecewise-quadratic bases was shown. Advantages of piecewise-quadratic bases: greater accuracy and good smoothness of approximation in comparison with piecewise-constant and piecewise-linear bases. The limitation of piecewise quadratic bases shows absence of fast algorithms for calculating coefficients. In order to overcome this limitation in given work, the method of calculation coefficients in Harmut’s piecewise-quadratic bases was proposed. The method is based on applications of good differential properties of basic splines, it is hardware-focused and allows to use existing algorithms of fast transformations in bases of orthogonal piecewise-constant functions for calculation of factors both piecewise-linear and piecewise-quadratic bases.

References:

1. HAAR, Zur Theorie der Orthogonalen Funktionensysteme, Math. Ann., 69(1910), 331–371.
2. Zalmanzon L. A. Transformation Fure, Uolsh, Haar and their applications in management, communications and other areas. — M.: the Science, 1989. — 496 p.
3. Chang-Kun Song, Kyung-Seok Kim. Efficient Signal Feature Detection using Spectral Correlation Function in the Fading channel. International Journal of Contents, vol.3, № 2, 2007, pp. 35–39
4. Bohan K. A., Koroleva N. A. Estimation parameters of efficiency two-dimensional transformations Haar // Electronic modelling. 2003. № 5. С.45 -56.
5. Zaynidinov H. N., Eeljin Chae, Tae Soo Yun. Application of Spectral Properties of Basic Splines in Problems of Processing of Multivariate Signals, International Journal of Contents, vol.3, № 4., December, 2007., p. 26–29.