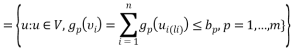Информационно-кибернетические исследования и проектирования сложных систем



Научно-технические революции способствовали усложнению функционирования различных процессов в жизни общества. Если раньше любой процесс описывался в рамках динамической системы, поведение объектов которой следовало простой логике и объяснялось обыкновенными или частными производными, то сейчас закономерность деятельности такого объекта зависит от множества переменных, которые не могут быть в полной мере учтены при модели исследования, опирающейся на обычные дифференциальные уравнения. Сегодня стало совершенно очевидным необходимость уделять особое внимание методам проектирования и исследования сложных систем.

Ключевые слова: метод, анализ, система, моделирование, процессы

Scientific and technological revolutions helped to complicate the functioning of various processes in the life of society. If earlier any process was described in the framework of a dynamic system whose behavior of objects followed simple logic and was explained by ordinary or partial derivatives, now the regularity of the activity of such an object depends on a set of variables that cannot be fully taken into account in the research model based on ordinary differential Equations. Today, it became absolutely obvious the need to pay special attention to the methods of designing and researching complex systems.

Keywords: method, analysis, system, modeling, processes

В настоящее время возникла необходимость разработки вычислительных алгоритмов, обеспечивающих наглядное отображение вопросов изучения многокритериальных целенаправленных процессов, формирующих сложную систему целенаправленного поведения. Актуальный вопрос исследования и проектирования систем заключается в выявлении проблем, возникающих в многофакторных системах, и рассмотрении путей их решения с помощью вычислительных методов исследования и проектирования сложных систем. Задачами данной публикации является поиск ответов на следующие вопросы:

1. Что такое сложная система и каковы ее основные характеристики?
2. В чем заключается специфика системного подхода и какие проблемы решаются с помощью него?
3. Какие методы исследования сложных систем существуют и как они применяются на практике?

Сложная система и ее основные характеристики

Сложная система [4] — это совокупность частей, интегрированные в одно целое согласно определенным принципам, зависящим друг от друга и связанным общими заданными отношениями. Данное определение не претендует быть едино правильным и точным, так как в настоящее время существует множество его вариаций, однако общая характеристика сложной системы у всех авторов практически идентична.

К отличительным характеристикам сложной системы можно отнести следующие особенности:

Во-первых, наличие большой совокупности подсистем, элементы которых связаны между собой и друг с другом. Какое-либо разделение системы на отдельные подсистемы носит практический характер, то есть не существует определенных правил, расчленение системы происходить только в зависимость от поставленных целей ее исследования. Необходимо отметить, что каждая подсистема должна быть сформирована таким образом, чтобы в ее пределах выполнялась какая-либо функция, то есть она должна представлять собой самостоятельно функционирующую часть.

Во-вторых, система должна обладать наличием большого количества связей между ее отдельными элементами как внутри подсистем, так и между ним в целом, то есть сложная система многомерна.

В-третьих, для сложной системы характерно наличие множества целей, сокрытых в ее подсистемах, и большое количество требований, предъявляемых системе из вне. В целом можно говорить, что сложная система многокритериальна.

В-четвертых, сложная система характеризуется разнообразием структур. Данное свойство связано с тем, что как внутри подсистем, так и между ними самими существуют различные способы структурирования элементов в одно целое, в том числе в систему в общем.

В-пятых, многообразие сущности подсистем, что определяется разнообразием их физической составляющей.

В итоге сложную систему справедливо охарактеризовать как многокритериальную, иерархично структурированную систему, все элементы которой подчинены выполнению единой для нее цели, обладающую многочисленными самостоятельными подсистемами различной природы.

Системный подход

В то время, когда появились первые научные труды, посвящённые характеристике сложной системы, определения ее места и роли в жизни общества, возникла и необходимость разработки методов ее изучения. Таким новым методом стал системный подход, заключающийся в совокупности методов, в том числе и вычислительных, рассматривающих сложные системы как взаимосвязанные элементы, формирующие единое ее целое.

Основная специфика системного подхода заключается в следующих особенностях:

1. описание отдельной подсистемы не носить самостоятельного характера, так как такой элемент системы описывается уже с учетом особенностей все сложной системы;
2. одна и также подсистема может выступать одновременно с различными характеристиками, показателями и т. д.;
3. при исследовании сложной системы необходимо помнить о неотъемлемости системы и среды, в которой она функционирует;
4. исследование свойств происходит либо в целом по всей системе, исходя из свойств отдельных подсистем, либо изучаются свойства подсистем, исходя из свойств всей системы в совокупности ее элементов;
5. процесс исследования систем носит математический или вычислительный характер;
6. при данном подходе всегда выбирается компромиссный вариант сложной системы, так как используется единая количественная мера, то есть единый показатель, который можно применить для характеристики всех подсистем;
7. особое внимание в исследовании уделяется согласованию всех подсистем, с целью достижения общих задач, поставленных перед сложной системой.

Существует ряд проблем, которые можно разрешить с помощью системного подхода.

Одной из таких проблем является создание единой количественной меры, которая бы была сформирована для всей системы в целом, исходя из множества показателей ее элементов. Для иерархичных сложных систем данная цель сводится к выбору компромиссного взаимоотношения и подчинения между различными уровнями системы. Для этого необходимо провести анализ свойств отдельных подсистем, исходя из свойств всей системы, что в свою очередь приводит необходимости определения требований к качеству результата деятельности подсистем.

В итоге качество функционирования подсистемы характеризуется динамическими величинами. С одной стороны, это является весьма важным показателем эффективной деятельность системы (если динамика положительная), однако, с другой стороны, качество деятельности системы не характеризуется лишь ее динамикой, необходимо учитывать и другие факторы, которые влияют на нее, например, стоимость оборудования, рабочее время, доступность ремонта, надежность использования и другие. Все они должным быть учтены при выборе проектируемой системы.

Существует несколько способов обнаружить такую систему, которая была бы лучше всех других по всем рассматриваемым показателям, однако обычно она отыскивается следующим образом. Предлагается изначальная система, которая должна быть «идеальной» исходя из всех требований, предъявленных к ней. Далее она испытывается различными способами, после чего делается заключение, является ли она подходящей. Если ответ отрицательный, в систему вносятся корректировки и заново тестируется. Так будет происходить до тех пор, пока не отыщется идеальная модель системы. Однако весь этот процесс может дать различные результаты, так как многое будет завесить о человека, проектирующего модель, от его опыта и других субъективных факторов.

К тому же в сложных иерархичных системах практически очень сложно выбрать общую стратегию действий между подсистемами различных уровней, двигаясь от наиболее важных целей к менее важным, так как в этом случае подсистемы начнут резонировать, то есть основные цели нижних подсистем будут игнорироваться или видоизменятся, что приведет к некорректному функционированию системы и быстрому ее выходу из строя.

Конфликт между подсистемами может быть решен двумя способами в зависимости от характера подсистем. Если подсистемы согласны на компромисс, то будет осуществлен поиск компромиссных стратегий между системами. В обратном случае, задача сводится к определению требуемого качества функционирования подсистем, то есть определению ограничений, выход за пределы которых уничтожит всю систему в целом.

Другая проблема, с которой сталкиваются при использовании системного подхода, само проектирование сложных систем. Многообразие подсистем, каждая из которых обладает своими функциями, требуют комплексного подхода, позволяющего проектировать систему в целом, а не по отдельным его частям. Суть проблемы заключается в длительности периода, в течение которого проектируется система, которая учитывается все многочисленные подсистемы с их самостоятельными целями, задачами и функциями. Процесс проектирования при системном подходе строится на основе деления на этапы таким образом, чтобы каждый последующий этап включал в себя больше информации о проектируемой системе. На каждом этапе существуют свои ограничения, которые должны быть устранены, следовательно, будет разработано множество пробных вариантов построения модели подсистемы до того, как будет выбран наилучший результат. Все это занимает большое количество времени, в следствии чего, к концу разработки модели может оказаться, что, либо части, либо вся система в целом безнадежно устарели. Чтобы избежать данного казуса, необходимо наличие эффективных алгоритмов системного подхода.

Основные задачи системного подхода при проектировании и исследовании сложных систем заключаются в следующем:

‒ формирование возможных альтернативных путей построения системы;

‒ разработка методов отклонения заранее неудовлетворяющих целям системы вариантов ее проектирования;

‒ формирование критериев оценки полученной системы;

‒ выбор наилучшего, компромиссного варианта.

Далее необходимо осветить некоторые вычислительные методы и алгоритмы решения описанных выше проблем применительно к проектированию сложных систем.

Методы решения задач многокритериальной оптимизации

В своей деятельности люди постоянно принимают какие-либо решения, то есть человек постоянно сталкивается с ситуациями, где необходимо выбрать один вариант из нескольких, который бы привел к достижению желаемой цели.

Таким ситуациям всегда присущи общие черты:

1. наличие переменных, которые выбираются человеком (управляющие воздействия), переменные, зависящие от выбора управляющих воздействий (выходные переменные), переменные, нерегулируемые человеком (параметры задачи), переменные, изменяющие вне зависимости от лица, принимающего решения (внешние возмущения), а также интервалы времени, на которых принимаются решения;
2. математическая модель;
3. ограничения, накладываемые как на параметры задачи, так и на внешние возмущения;
4. критерий оптимальности (целевая функция), с помощью которой возможна оценка выбранной решения.

Если формулировать задачу выбора с помощью математического языка, то она будет представлена в виде математической модели следующего вида:

y: P ⋅ U ⋅ Ω⟶Y

где

U — множество векторов управляющих воздействий

P — множество векторов параметров

Y — множество векторов выходных переменных

Ω — множество векторов внешних возмущений

Примером построения математической модели может быть задача о диете, которая формулируется следующим образом. Имеется n-ое количество продуктов А1,...,Аn. Нужно определить, суточное потребление каждого из этих продуктов и оценить, сколько полезных веществ будет получено организмом после их употребления в течение суток.

Параметрами данной задачи будут являться сами виды продуктов и количество полезных веществ в единице. Выходными переменными станут полезные вещества, но в совокупности, то есть после употребления набора продуктов. Также предполагается, что возмущения (например, порча продуктов) не рассматриваются в данном случае.

Далее необходимо отобразить условия с помощью векторов. Вектор у = {yi}(i=1,…,m) — это набор питательных веществ, необходимых в рационе, pi={pij}(i=1,…,m; j=1,…,n) — это вектор, характеризующий количество полезных веществ в одной единице продукта, а через вектор u={ui}(i=1,...,n) отображается количество продуктов, необходимое для человека. Отсюда можно вывести формулу, которая и будет являться математической моделью задачи:

yi=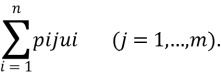

Теперь необходимо определить систему ограничений и построить целевую функцию или оптимальный (идеальный) вариант, отталкиваясь от которого будет принято какое-либо решение.

В данной задачи ограничением будет являться необходимое количество каждого питательного вещества и цена единицы продукта, то есть выбор будет заключаться в том, чтобы было получено достаточно питательных веществ при минимальных стоимостных затратах. Стоимость суточного потребления будет равна:

F(u)=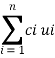, где ci (i=1,…,m) — это цена единицы продукта.

Ограничения могут быть представлены одним из следующих способов (таблица 1). Данное обстоятельство зависит от типа математической модели ограничения.

Таблица 1

Типы математической модели ограничения

Статистическая модель снепрерывными управляющими воздействиями u={ui}(i=1,...,n)	Статистическая модель сдискретными управляющими воздействиями	Динамическая модель синтервалом времени
нелинейные ограничения: , где b — вектор-столбец констант ограничений, а g(u) — нелинейные и непрерывно дифференцируемые функции	D Где V — декартово произведение конечных множеств Ui,) — произвольные функции дискретного аргумента	Ограничения Dt с непрерывным временем определяются: - Дифференциальными связям, записанными в силу динамики изменения выходных переменных: - Условиями траектории движения, определяемые в том числе краевыми условиями: • l=0,1,…, • l=0,1,…,
линейные ограничения: Где А — заданная матрица размерности m x n, а — нижняя и верхняя границы изменения компоненты вектора управляющих воздействий		Интервал времени , на котором принимается решение, может быть дскретным образом с шагом ∆Т: , где М — число шагов, на которое принимается решение
смешанные ограничения:

Задача выбора возникает, когда управляющее воздействие не единственно. Такую совокупность управляющих воздействий, отвечающую всем условиям и подходящим по всем ограничениям, принято называть множеством альтернатив А. Выбор той или иной альтернативы зависит от свойств конкретных альтернатив, которые находят отображение в целевой функции. Следует учитывать и тот факт, что задание только одного свойства не всегда способно достоверно отобразить ситуацию, поэтому для того, чтобы был выбран наилучших вариант, необходимо учитывать одновременно несколько различных свойств альтернатив.

В целом принятие сложного решения может быть сведено к выбору альтернативы, которая не является оптимальной ни для одной функции цели, но оказывается приемлемой для всей совокупности функций цели, то есть к нахождению компромиссной альтернативы или пути решения поставленной задачи.

Приемлемой альтернатива будет считаться только в том случае, если отклонения от оптимального значения по каждой функции цели

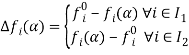
достигает возможного минимума.

Далее необходимо рассмотреть метод ограничений при поиске компромиссных решений в задачах векторной оптимизации. Для обоснования вычисленных действий данного метода используется теорема [3], которая заключается в том, что компромиссное решение для минимального значения параметра , характеризующего совместимость системы, может быть только одно.

Для нахождения компромиссного решения необходимо рассмотреть повторяющиеся процессы с параметром , где на каждом шаге повторяется совместимость неравенств для и заданного вектора р.

(1)

Параметр ограничивает относительные потери, при этом, если , то и потери стремятся к нулю, а функция цели достигает своих оптимальных значений, если же , то будут удовлетворятся неравенства (1). Только при условии уменьшения параметра возможно достигнуть альтернативы, обеспечивающей минимальные потери по целевой функции и являющейся компромиссным решением задачи.

Процесс применения повторяющихся действий останавливается, когда наименьшее (т) (где т — номер шага), при котором система совместна, отличается от своего ближайшего значения , при котором совместимости уже нет, не больше, чем на . Если решение системы единственное, то оно и будет искомой компромиссной альтернативой, если же нет, то необходимо провести оптимизацию на множестве эквивалентных решений с точностью до какого-либо обобщенного критерия. Например, можно выбрать следующий критерий:

и заняться его минимизацией на множестве альтернативных решений:

A’={}

Однако это одни из способов нахождения единственно верного решения. Так, если для целей преобразования функции выбрать соотношения

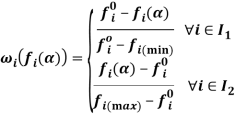
где и — наименьшие значения максимизируемых инаибольшие значения минимизируемых функций цели

то решение задачи параметрического программирования относительно параметра при векторе предпочтений p может выглядеть следующим образом:

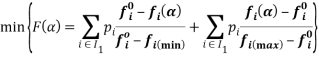
с учетом ограничений:

1. 
2. 

Решение данной задачи поможет определить компромиссное решение для задачи.

Использование вычислительных методов для построения сложных систем на примере систем технического зрения мобильных колесных роботов

Восприятие окружающей действительности во время движения мобильных колесных роботов (МКР) — задача довольно сложная, которая зависит от ряда факторов таких, как: конструкция самого робота, проектирования структуры его технического зрения (СТЗ), качество эксплуатации. Любое конструкторское решение, которое будет способствовать модификации робототехники, принесет дополнительные затраты, возрастающие по мере усложнения систем его функционирования.

Для того, чтобы правильно решить задачу проектирования такого МКР, которая заключается возможной в минимизации издержек при усложнении систем робота, необходимо сформулировать ее как оптимизационную задачу. В качестве критериев могут быть использованы факторы, влияющие на процесс создания систем технического зрения МКР (условия эксплуатации в том числе тип и вид рельефа, на котором будет эксплуатироваться МКР, система управления, скорость и др), то есть стоимостные и эксплуатационные характеристики, а в качестве ограничений — система зависимостей, прессующая роботу и его СТЗ.

Для математического представления данной задачи аргументами будут являться векторы пространственных координат (x, y, z), угловые координаты — () и время t, а функция есть ни что иное как аналитические зависимости, описывающие движение МКР.

Область определения как для СТЗ, так и для функций не должна выходит за рамки следующих ограничений:

‒ угловые размеры поля зрения объективов (для пространственного сигнала Ф (x,y,z,,t);

‒ площадь фоточувствительного сигнала с зарядовой связью (для сигнала В(Y,Z);

‒ время накопления зарядов в ячейке (для сигнала (t)).

Для области значений так же существуют свои ограничения, такие как:

‒ характеристики оптической системы (для сигнала В(Y,Z);

‒ характеристика фоточувствительного прибора с зарядовой смесью (ФПЗС) (для сигнала (t)).

Все сигналы на каждом этапе могут считаться непрерывными. В качестве функции цели или критерия сравнения автором статьи [5] была выбрана мера, являющаяся носителем физического смысла квадрата евклидова расстояния:

‒ для двумерных сигналов ;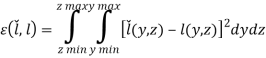

‒ для одномерных сигналов ,

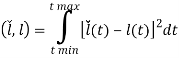где - функция пространственных координат, формируемая реальной системой, — идеальная функция, — функция времени, формируемая реальной системой, — идеальная функция соответственно.

Затем необходимо преобразовать функции, для данной цели используется преобразование по Фурье, которое будет выглядеть следующим образом:

‒ для двумерной функции ;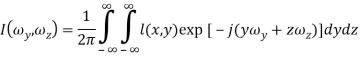

‒ для одномерной функции ,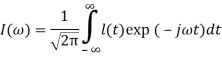

где — круговые частоты пространственного гармонического сигнала, — круговая частота временного гармонического сигнала, j= –мнимая единица.

Для того, чтобы перейти из спектральной сферы в сигнальную, нужно еще раз преобразовать функции Фурье, которые будут иметь следующую форму:

‒ для двумерной функции ;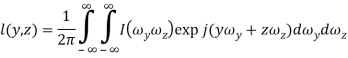

‒ для одномерной функции ,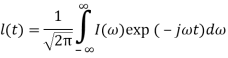

Далее рассматриваются применение частотных моделей сигналов, которые помогают при исследовании и построении СТЗ и МКР:

1. заменить вычисление интегралов свертки произведением спектральных характеристик;
2. применить методику, основой которой является задача Коши, для решения дифференциальных уравнений;
3. использовать единый аппарат придаточных функций.

Все это в совокупности значительно упрощает исследование задачи СТЗ МКЗ.

В последнее время огромное внимание уделяется проектированию и анализу сложных систем. Одним из способов их изучения является системный подход, который включает в себя различные вычислительные методы построения и исследования сложных систем.

В работе были проанализированы основные характеристики сложных систем и выявлен ряд проблем, возникающих в многофакторных системах, а именно:

1. нахождение компромиссного взаимодействия подсистем сложной системы на всех ее уровнях, позволяющего сделать наилучший выбор, который приведет к созданию наиболее эффективно действующей модели системы в целом;
2. затраты большого количества времени при проектировании алгоритмов сложных систем, которые зависят от наличия колоссального числа связей как между подсистемами системы, так и между элементами самих подсистем.

Данные проблемы могут быть решены при наличии эффективных алгоритмов системного подхода.

На примере задачи оптимизации рациона человека, соблюдающего диету, были проиллюстрированы методы решения задач многокритериальной оптимизации. Основа методов сводится к выявлению и соблюдению следующих этапов при нахождении оптимального решения:

1. выявление переменных, которые будут оказывать существенное воздействие на систему;
2. создание математической модели;
3. добавление ограничений в созданную модель;
4. отбор определенных оптимальных решений, основываясь на сравнение с которыми приминаются компромиссные решения.

В целом значимость и эффективность вычислительных методов проектирования и оценки эффективности деятельности сложных систем были проиллюстрированы на примере построения систем технического зрения мобильных колесных роботов. Данные методы значительно упрости задачу проектировщика по разработки наиболее технически сложных СТЗ МКЗ при минимизации затрат на их создание и эксплуатацию, что свидетельствует о эффективности применения данных методов при решении подобных задач.

Литература:

1. Cyberleninka [Электронный ресурс]. — Режим доступа: http://cyberleninka.ru, свободный;
2. Elibrary [Электронный ресурс]. — режим доступа: http://elibrary.ru/defaultx.asp, свободный;
3. Михалевич В. С., Волкович В. Л. «Вычислительные методы исследования и проектирования сложных систем», М.: Наука. Главная редакция физико-математической литературы, 288 с.;
4. Н. П. Бусленко, словарная статья «Сложная система» [Электронный ресурс]. — Режим доступа: http://victor-safronov.ru/systems-analysis/glossary/complex-system.html, свободный.
5. Статья «методы исследования и проектирования систем технического зрения мобильных колесных роботов» автор Акименко Т.А., журнал «Известия Тульского государственного университета. Технические науки», 2014 год