Система дополнительного образования по математике часто направлена на выявление талантливых обучающихся. Поэтому такое образование предполагает подготовку учащихся к участию в различных математических олимпиадах. При этом, если сравнить количество учащихся (1 группа), желающих участвовать в олимпиадах, и количество учащихся (2 группа), успешно справляющихся с решением олимпиадных задач, то ни для кого не секрет, что в 5–6 классах количество учащихся 1 группы в разы превышает количество учащихся 2 группы. Диаграмма составлена по данным участия в школьном этапе учащихся филиала в 2019 году
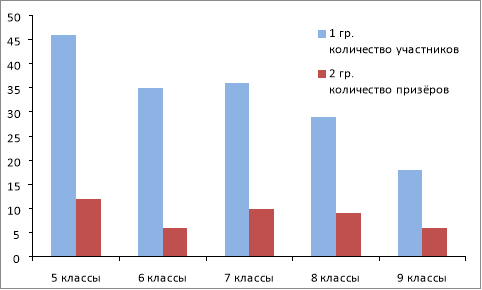
По диаграмме видно, что от класса к классу наиболее быстро убывает количество учащихся именно 1 группы. Здесь много причин, в том числе и формирование адекватной самооценки. Но немалую роль играет и падение интереса к решению нестандартных задач. Введение в систему дополнительного образования занятий, опосредованно связанных с математикой, поддерживает интерес учащихся к предмету, помогает расширить математический кругозор учащихся, не даёт потерять веру в свои силы. В первую очередь, говоря о таких занятиях, я имею в виду знакомство учащихся с миром головоломок, как механических (кубик Рубика разных размерностей и др.), так и аналитических.
К наиболее популярным аналитическим головоломкам сейчас можно отнести те, которые печатаются в развлекательных журналах — судоку и нонограммы. Но эти журналы, в основном, интересуют лишь взрослую аудиторию. Задания в таких изданиях рассчитаны на сосредоточенную длительную кропотливую работу, умение добиваться поставленной цели, а иногда и умения отступиться, признать своё поражение. В периодических изданиях, адресованных детям, таких головоломок практически нет.
В этом учебном году коллективом моих единомышленников была разработана система занятий математического кружка для 5–6 классов «Японские головоломки», где, начиная с азов, подробно рассматривается решение таких японских головоломок, как судоку, какуро, нонограмма.
Остановлюсь наиболее подробно на занятиях, посвящённых решению нонограмм. К нонограммам или японским кроссвордам относят рисунки на клетчатой бумаге, зашифрованные с помощью цифр.
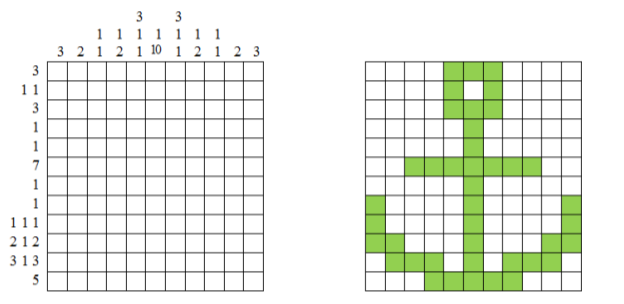
Для решения нонограммы используются два способа — аналитический и метод «от противного». В начале учебного года было проведено тестирование учащихся 5–9 классов на предмет умения решать нонограммы. Учащимся для решения была предложена простейшая нонограмма. В результате выяснилось, что в училище только один девятиклассник знает о существовании таких головоломок. Для сравнения: на момент исследования кубик Рубика размерностью 3х3 только среди 160 учащихся 5–6 классов умеют собирать 42 ученика. И их количество постоянно растёт! Такой результат связан, конечно, не с трудностью решения нонограмм, а с их малой распространённостью среди подростков.
Аналитический метод решения предусматривает нахождение закрашенных и пустых клеток. Рассмотрим основные аналитические методы решения.
Есть строки (столбцы), в которых можно сразу расположить закрашенные клетки, так как такое расположение единственно:
|
2 4 3 | |||||||||||
|
| |||||||||||
|
2 4 3 |
Есть строки (столбцы), в которых можно выделить клетки, являющиеся точно закрашенными. Например, блок из пяти клеток может располагаться в строке одним из четырёх способов, но при любом способе две центральные клетки будут закрашенными, так как блок должен быть хотя бы на одну клетку длиннее половины строки:
|
5 | ||||||||
|
| ||||||||
|
|
|
Если в строке (столбце) два блока клеток, то розовым цветом выделим область перемещения для первого блока из четырёх клеток:
|
4 3 |
И здесь можно выделить всегда закрашенную клетку:
|
4 3 |
Жёлтым цветом выделим область перемещения второго блока из трёх клеток:
|
4 3 |
Здесь нет клеток, закрашенных при любом положении блока. В результате решение такой строки (столбца) выглядит так:
|
4 3 |
Если удалось закрасить клетки в крайних строках (столбцах), то это даёт возможность закрасить некоторые клетки в столбцах (строках) и определить пустые клетки (отмечены точками):
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 | |
|
3 2 | ||||||||
|
| ||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 | |
|
3 2 | ||||||||
|
· |
· | |||||||
|
· |
· |
· |
Иногда удаётся выделить пустые клетки, если можно доказать, что блок закрашенных клеток до них не дойдёт:
|
4 |
· |
|
|
· |
· |
· |
могут быть закрашены
После знакомства с основными аналитическими методами обучающимся предлагается выполнить практическую работу № 1.
Определите в каждой строке (если это возможно) закрашенные или пустые клетки:
|
1) |
8 |
|
|
|
|
|
|
|
2) |
10 |
|
|
|
|
|
|
|
3) |
7 |
|
|
|
|
|
|
|
4) |
6 |
|
|
|
|
|
|
|
5) |
7 |
|
|
|
|
|
|
|
|
|
|
6) |
74 |
|
|
|
|
|
|
|
|
|
7) |
37 |
|
|
|
|
|
|
|
|
|
8) |
29 |
|
|
|
|
|
|
|
|
|
|
9) |
77 |
|
|
|
|
|
|
|
|
|
|
10) |
437 |
|
|
|
|
|
|
|
|
|
|
|
11) |
6 |
|
|
|
|
|
|
|
|
|
|
12) |
6 |
|
|
|
|
|
|
|
|
|
|
13) |
57 |
|
|
|
|
|
|
|
|
14) |
8 |
|
|
|
|
|
|
|
|
15) |
64 |
|
|
|
|
|
|
|
|
|
16) |
4 |
|
|
|
|
17) |
|
| |||||||
|
|
|
| |||||||
|
|
|
| |||||||
|
|
|
| |||||||
|
|
2 |
3 |
1 |
3 |
3 |
1 |
2 |
2 |
|
18) |
6 |
| |||||||
|
|
3 |
| |||||||
|
|
2 |
| |||||||
|
|
4 |
| |||||||
|
|
2 |
При выполнении этой работы автоматизируются навыки решения нонограмм. Затем учащимся предлагается выполнить четыре практических работы, в которых нонограммы расположены в порядке увеличения трудности решения.
Знакомство с методом «от противного» происходит на этапе, когда обучающиеся уже научились решать простые нонограммы небольшой размерности. Метод «от противного» предполагает, что какая-либо клетка (или группа клеток) закрашена, и, продолжив решение, приходим к противоречию, либо убеждаемся, что закраска была правильной.
|
3 |
1 1 |
4 1 1 |
6 3 |
4 1 1 |
1 1 |
3 | |
|
1 |
· |
· |
· |
· |
· |
· | |
|
3 |
· |
· |
· |
· | |||
|
3 |
· |
· |
· |
· | |||
|
1 3 1 |
· |
· | |||||
|
1 3 1 |
· |
· | |||||
|
1 1 1 |
· |
· |
· |
· | |||
|
1 1 |
· |
· | |||||
|
3 |
· |
· | |||||
|
1 |
· |
· |
· |
· |
· |
· | |
|
5 |
· |
· |
Например, если закрасить три клетки слева, отмеченные крестиками, то тогда в строке сверху невозможно разместить две единичные клетки. Если попробовать такую же группу клеток слева, то придём к такому же выводу. Значит, эта группа клеток будет закрашена по центру:
|
3 |
1 1 |
4 1 1 |
6 3 |
4 1 1 |
1 1 |
3 | |
|
1 |
· |
· |
· |
· |
· |
· | |
|
3 |
· |
· |
· |
· | |||
|
3 |
· |
· |
· |
· | |||
|
1 3 1 |
· |
· | |||||
|
1 3 1 |
· |
· | |||||
|
1 1 1 |
· |
· |
· |
· | |||
|
1 1 |
· |
· |
· |
· |
· | ||
|
3 |
· |
· |
· |
· | |||
|
1 |
· |
· |
· |
· |
· |
· | |
|
5 |
· |
· |
Решение нонограмм также даёт и простор для собственного творчества обучающихся. Создание собственных нонограмм — это не просто творческий процесс, ведь необходимо не только придумать красивый рисунок и зашифровать его с помощью цифр, но и проверить, действительно ли при решении получившейся нонограммы получается задуманный рисунок, т. е. проверить нонограмму на единственность её решения.
Задавшись вопросом единственности решения, мы с обучающимися пришли к необходимости поиска факторов, влияющих на разрешимость нонограммы (т. е. на существование единственного решения этой головоломки). В результате обучающимися была проведена исследовательская работа по поиску этих факторов, результаты которой были представлены на научно-практических конференциях школьников разного уровня.
В числе факторов, влияющих на неразрешимость нонограмм, были определены разреженность рисунка нонограммы и использование внутри рисунка единичных квадратов в нонограмме (квадратов, в которых в каждой строке и каждом столбце закрашено по одной клетке).
В результате планомерной работы по решению нонограмм у учащихся постепенно формируется стойкий интерес к решению японских головоломок, а также нестандартных логических задач. Положительные эмоции, которые обучающиеся получают, разгадав очередную нонограмму, помогают им лишний раз увидеть свои возможности. Решение каждой следующей нонограммы — это преодоление себя, воспитания стремления добиваться поставленной цели, тренировка логического мышления.
В целом весь курс решения японских головоломок рассчитан на раскрытие и развитие как математического мышления и исследовательских способностей, так и других качеств личности — терпения, умения ставить цель и добиваться её достижения, умения критически анализировать свои действия и искать допущенные ошибки.

