Исследование процессов лучистого теплообмена в излучающих системах различной конфигурации с поглощающей средой

Теория переноса излучения и лучистого теплообмена представляет собой одну из важнейших областей общей теории необратимых процессов. Разработана математическая строгая общая теория переноса излучения и лучистого теплообмена.

Разнообразие математических методов, используемых в теории лучистого теплообмена, определяется многообразием ее применения в различных областях естествознания и техники, и прежде всего в астрофизике, высокотемпературной теплофизике, теплоэнергетике, теплотехнике различного рода промышленных печей, ядерной энергетике, авиационной и космической технике.

В связи с разработкой проблем теории переноса излучения и лучистого теплообмена, связанных с различными и многообразными ее приложениями, были созданы научные школы, разрабатывающие и развивающие различные научные направления в этой области. К числу основных и важнейших направлений дальнейших теоретических исследований проблем лучистого теплообмена следует отнести развитие и широкое применение обобщенного зонального метода теории лучистого теплообмена к определению основных характеристик поля излучения в излучающих системах различной конфигурации, заполненных поглощающей и анизотропно рассеивающей средой.

Применение указанного метода позволяет произвести численное исследование и всесторонний анализ тепловой работы.

В данной работе дано применение метода приближенного решения интегральных уравнений излучения, разработанного профессором Ю. А. Суриновым, к численному решению различных постановок задачи о лучистом теплообмене в излучающих системах различной конфигурации. При этом рассматриваются следующие системы, состоящие из четырех оптически однородных серых тел, разделенных изотермической поглощающей средой:

а)     камера прямоугольного сечения бесконечной длины (нижнее основание — зона 1, боковые поверхности — зона 2 и 3, верхнее основание — зона 4);

б)     цилиндрическая камера конечной длины, нижнее и верхнее основания которой составляют зоны 1 и 4, а боковая поверхность подразделена на две зоны — 2 и 3.

Поглощающая среда, заполняющая излучающую систему, составляет объемную зону 5.

Заданы температура среды и коэффициент объемного поглощения среды. Известны геометрические размеры и коэффициенты поглощения отдельных зон системы.

В зависимости от способов задания граничных условий рассматриваются следующие постановки задачи о лучистом теплообмене:

а)     фундаментальная — задаются температуры всех граничных тел;

б)     первая смешенная — для тела 2 задается безразмерная плотность результирующего изучения, а для остальных тел системы — температуры;

в)     вторая смешенная — для граничных тел 2 и 3 задаются безразмерные плотности результирующего излучения, а для тел 1 и 4 — температуры Т₁, Т₄.

Решение интегральных уравнений изучения приводит к следующим выражениям, представленным в безразмерном виде.

а)     ) для фундаментальной постановки задачи

Θ_рез (М₁)=(1)

Θ_рез(М₂)=(2)

Θ_рез(М₃)=(3)

Θ_рез(М₄)=(4)

б)    для первой смешанной постановки задачи

Θ_рез(М₁)=(5)

Θ_рез(М₃)=(6)

Θ_рез(М₄)=(7)

Θ_рез(М₂)=(8)

в)    для второй смешанной постановки задачи

Θ_рез(М₁)=(9)

Θ_рез(М₄)=(10)

Θ(М₂)=(11)

Θ_рез(М₃)=(12)

где Θ(М₂) =Θ(М₃) =

Θ₂₁ =Θ₃₁ =Θ₄₁ =

Θ_рез,2 =Θ_рез,3 =

Аналогичные выражения можно получить для осредненных характеристик лучистого теплообмена.

Результирующий лучистый поток поглощающей среды определяется исходя из уравнения:

где Θ_рез,5 = -(Θ_рез,1 + Θ_рез,2 + Θ_рез,3 + Θ_рез,4)

Θ_рез,i = Е_рез,iF_i (I = 1, 2, 3, 4)

Е_{рез,i —} плотность результирующего лучистого потока данного тела.

Локальные разрешающие угловые коэффициенты излучения Ψ(M_i,F_к) определяются решением конечной системы алгебраических уравнений:

а) для фундаментальной постановки задачи

Ψ(M_i,F_к) — R₁Ψ(M_i,F₁) Ψ _1к — R₂Ψ(M_i,F₂) Ψ _2к — R₃Ψ(M_i,F₃) Ψ _3к — R₄Ψ(M_i,F₄) Ψ _4к = Ψ(M_i,F_к)       (13)

б) для первой смешанной

Ψ(M_i,F_к) — R₁Ψ(M_i,F₁)Ψ_1к — Ψ(M_i,F₂) Ψ_2к — R₃Ψ(M_i,F₃)Ψ_3к — R₄Ψ(M_i,F₄)Ψ_4к = Ψ(M_i,F_к) (i, к = 1, 2, 3,4)                                                                                                                                                     (14)

в) для второй смешанной

Ψ(M_i,F_к) — R₁Ψ(M_i,F₁)Ψ_1к — Ψ(M_i,F₂) Ψ_2к — Ψ(M_i,F₃)Ψ_3к — R₄Ψ(M_i,F₄)Ψ_4к = Ψ(M_i,F_к) (i, к = 1, 2, 3,4)                                                                                                                                                    (15)

В работе определена локальная разрешающая поглощательная способность Ы(M₁V) — есть доля поглощенного средой лучистого потока, направленного от элемента поверхности системы, с учетом поглощений, обусловленных многократными отражениями системы.

Определяется эта характеристика на основании следующих оптико-геометрических уравнений замкнутости:

Ы(M_iV) = 1 — 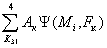 (M_iЄF_i, i = 1, 2, 3,4)                                                             (16)

В работе получены поля знаний локальной поглощательной способности среды А(M_iV) = 1 — и локальной поглощательной разрешающей способности среды Ы(M_iV) для разных постановок задачи. Равенство А(M_iV) = Ы(M_iV) выполнимо только в случае фундаментальной постановки задачи при условии, что все граничные тела являются черными. Для всех других постановок задачи А(M_iV) всегда меньше Ы(M_iV).

Локальные и средние обобщенные угловые коэффициенты изучения Ψ(M_i,F_к) и Ψ_iк определены для случая плоской задачи на основании приближенных методик. Численные значения в прилагаемых таблицах.

Используя полученные формулы и выражения, можно произвести численные расчеты локальных и средних характеристик излучения для рассмотренной постановки задачи с различными вариантами геометрических, оптических, температурных и энергетических параметров излучающих систем.

Результаты расчетов различных характеристик лучистого теплообмена в камере прямоугольного сечения бесконечной длины для фундаментальной постановки задачи, произведенные на ЭВМ, приведены в таблицах.

Результаты проведенного исследования могут найти применение в тепловых расчетах различных теплотехнических устройств.

Требования современной науки и техники заставляют все чаще обращаться к задачам теплообмена изучением с учетом поглощающей среды, заполняющей системы различной конфигурации.

Решена обобщенная задача о теплообмене излучением как для граничных, так и для объемных зон с диффузными оптическими свойствами.

Исследование выполнено для локальных разрешающих и энергетических характеристик прямоугольной камеры и локальных угловых коэффициентов излучения цилиндрической системы. Результаты численного исследования приведены в виде таблиц и графических зависимостей в безразмерн6ом виде.

Результаты работы с учетом последующих этапов исследования в этом направлении могут быть использованы при расчетах и проектировании промышленных печей (электрических печей сопротивления), для расчета сушильных процессов и других способов обработки сырья и полуфабрикатов пищевой промышленности, при исследовании тепловой работы различных нагревательных устройств, где лучистый теплообмен играет ведущую роль.

Средние угловые коэффициенты излучения для излучающей системы, состоящей из четырех зон (прямоугольная камера бесконечной длины h = )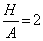

Z=2A	Ψ12= Ψ42= Ψ13= Ψ13	Ψ41= Ψ14	Ψ21= Ψ31= Ψ24= Ψ34	Ψ32= Ψ23	Ψ11= Ψ22= Ψ33= Ψ44
0,1	0,3455	0,1765	0,1726	0,5281	0,000
0,5	0,2432	0,0728	0,1216	0,3014	0,000
0,9	0,1821	0,0369	0,0910	0,1798	0,000
1,3	0,1428	0,02111	0,0714	0,1093	0,000
1,7	0,1160	0,0130	0,0580	0,6788	0,000

Локальные обобщенные угловые коэффициенты излучения в излучающей системе, состоящей из четырех зон (прямоугольная камера бесконечной длины)

Z=2A	х, у	Ψ(М1, F2) Ψ(М4, F2)	Ψ(М1, F3) Ψ(М4, F3)	Ψ(М1, F4) Ψ(М4, F1)	Ψ(М2, F1) Ψ(М3, F1)	Ψ(М4, F1) Ψ(М3, F2)	Ψ(М2, F4) Ψ(М3, F4)	Ψ(М1, F1) Ψ(М4, F2) Ψ(М3, F3) Ψ(М4, F4)
0,1	0	0,5000	0,2305	0,1708	0,5000	0,3767	0,0405	0,000
	0,2	0,4225	0,2686	0,1815	0,2903	0,5213	0,0611	0,000
	0,4	0,3634	0,3123	0,1872	0,1654	0,5969	0,0976	0,000
	0,6	0,3126	0,3634	0,1872	0,0976	0,5969	0,1654	0,000
	0,8	0,2683	0,4225	0,1815	0,0611	0,5213	0,2903	0,000
	1,0	0,2305	0,5000	0,1708	0,0405	0,3767	0,5000	0,000
0,9	0	0,5000	0,0622	0,0253	0,5000	0,1203	0,0057	0,000
	0,2	0,2736	0,0872	0,0276	0,1606	0,1779	0,0122	0,000
	0,4	0,1799	0,1288	0,0288	0,0642	0,2058	0,271	0,000
	0,6	0,1238	0,1799	0,0288	0,0271	0,2058	0,0642	0,000
	0,8	0,0872	0,2736	0,0276	0,0122	0,1779	0,1606	0,000
	1,0	0,0622	0,5000	0,0253	0,0057	0,1203	0,5000	0,000

Численные значения безмерной локальной плотности результирующего излучения для фундаментальной постановки задачи о лучистом теплообмене в прямоугольной камере бесконечной длины

Z=2A	хх, у	А1=0,9; А2=0,85; А5=0,8; А4=0,7 Θ21=0,2; Θ31=0,15; Θ41=0,6				А1=А4=1; А2=0,85; А3=0,8 Θ21=0,2; Θ31=0,15; Θ41=0,6
		Θрез=(М1)	Θрез=(М2)	Θрез=(М3)	Θрез=(М4)	Θрез=(М1)	Θрез=(М2)	Θрез=(М3)	Θрез=(М4)
0,1	0	0,6695	0,5694	0,6182	0,2471	0,7426	0,5612	0,6137	0,3517
	0,2	0,6851	0,5888	0,6267	0,2480	0,7602	0,5836	0,6238	0,3529
	0,4	0,6939	0,6004	0,6318	0,2485	0,7700	0,5969	0,6297	0,3534
	0,6	0,6991	0,6087	0,6359	0,2484	0,7757	0,6055	0,6340	0,3535
	0,8	0,7006	0,6166	0,6406	0,2483	0,7774	0,6128	0,6380	0,3532
	1,0	0,6965	0,6251	0,6460	0,2477	0,7728	0,6197	0,6423	0,3526
0,9	0	0,7274	0,5929	0,6331	0,2597	0,8073	0,5846	0,6288	0,3708
	0,2	0,7932	0,6400	0,6571	0,2665	0,8805	0,6372	0,6556	0,0380
	0,4	0,8148	0,6520	0,6630	0,2685	0,9045	0,6507	0,6623	0,3833
	0,6	0,8205	0,6566	0,6653	0,2686	0,9109	0,6554	0,6643	0,3836
	0,8	0,8121	0,6582	0,6662	0,2669	0,9016	0,6562	0,6648	0,3811
	1,0	0,7719	0,6536	0,6635	0,2606	0,8568	0,6477	0,6595	0,3722

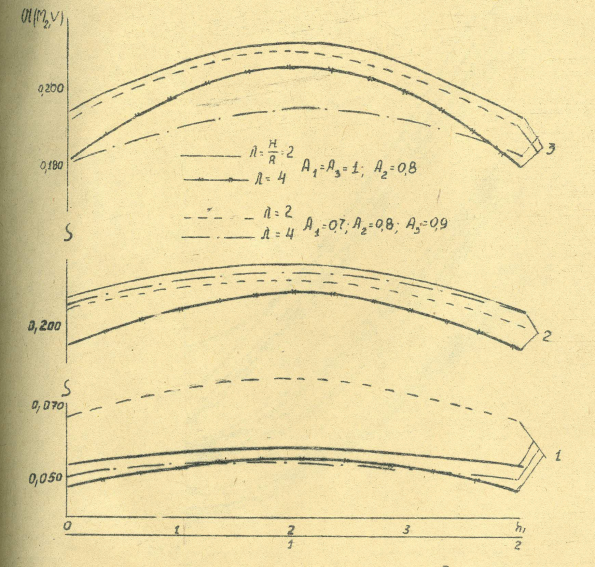
Зависимость Ы(М₂V) от h₁ = 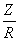 для цилиндра (λ = 2; 4), заполненного чисто поглощающей средой с dR = 0,05(1); 0,1(2); 0,2(3)

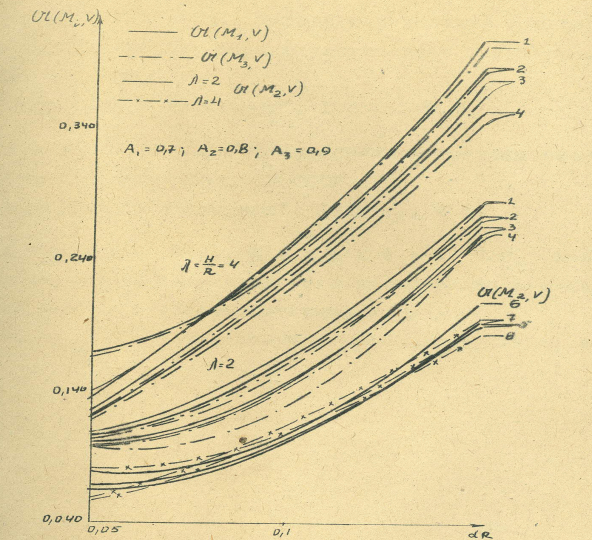
Зависимость Ы(М_iV) от dRдля цилиндра (λ = 2; 4), заполненного поглощающей средой при r = 0(1); 0,5(2); 0,8(3); 1(4); h=0(5); 1(6); 2(7); 4(8)

Литература:

1.          Суринов Ю. А. Методы определения и численного расчета локальных характеристик поля излучения. Изв. АН СССР. «Энергетика и транспорт», 1965. № 5.

2.          Суринов Ю. А. К определению поглощательной способности среды. Изв. АН СССР. «Энергетика и транспорт», 1967. № 4.

3.          Суринов Ю. А., Киселева Е. С. Исследование характеристики лучистого теплообмена в цилиндрической камере с учетом поглощения среды. Изв. АН СССР. «Энергетика и транспорт», 1971. № 6.