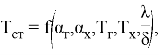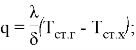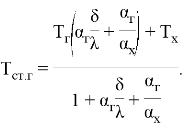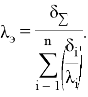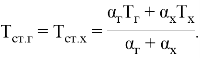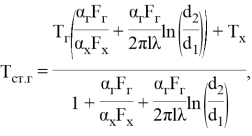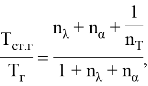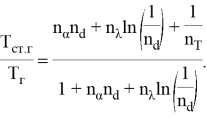Теплообменные установки (ТУ) широко применяются в энергетике, транспортной, химической и других отраслях промышленности и имеют разнообразные конструкции, зависящие от условий работы и предъявляемых к ним требований. Интенсивное развитие техники, в том числе ракетно-космической, в настоящее время характеризуется выдвижением современных требований к ТУ. Для решения новых задач необходимо создание усовершенствованных ТУ, обеспечивающих оптимальное сочетание тепловой эффективности, технологичности, удобства эксплуатации и минимальной стоимости.
Проблема разработки эффективной теплоэнергетической установки или аппарата обычно связана с необходимостью проведения огневых испытаний зачастую при достаточно высоких температурах. В связи с этим актуальной становится оценка температурного состояния поверхности теплообмена при различных режимах нагрева и охлаждения.
Целью настоящей работы является прогнозирование состояния объекта испытания и системы измерения и планирование режимов безаварийного испытания теплообменных трактов.
Задачи исследования:
- на основании теории тепломассообмена изучить методы определения температур поверхности теплообмена;
- получить расчетные зависимости для исследования температуры стенки;
- проанализировать степень влияния различных режимных и конструктивных параметров тракта на температурное состояние стенки.
Согласно известным закономерностям теплопереноса, температура стенки, как целевая функция исследования, представляется в виде зависимости, отражающей режимы нагрева и охлаждения.
|
|
(1) |
где ![]() температуры горячего и холодного теплоносителей соответственно, К;
температуры горячего и холодного теплоносителей соответственно, К; ![]() температура поверхности стенки, К;
температура поверхности стенки, К; ![]() коэффициент теплоотдачи от горячего теплоносителя к стенке, Вт/(м2
коэффициент теплоотдачи от горячего теплоносителя к стенке, Вт/(м2![]() К);
К); ![]() коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м2
коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м2![]() К);
К); ![]() коэффициент теплопроводности стенки, Вт/(м
коэффициент теплопроводности стенки, Вт/(м![]() К);
К); ![]() толщина стенки, м.
толщина стенки, м.
На основании закона Ньютона-Рихмана и закона Био-Фурье для стенки можно записать следующие расчетные формулы:
|
|
(2) | |
|
|
(3) | |
|
|
(4) |
где ![]() плотность теплового потока, Вт/м2;
плотность теплового потока, Вт/м2; ![]() температура горячей поверхности стенки, К;
температура горячей поверхности стенки, К; ![]() температура холодной поверхности стенки, К.
температура холодной поверхности стенки, К.
На основании баланса тепловых потоков получена следующая зависимость для температуры горячей поверхности теплообмена, например, плоской стенки, при граничных условиях III рода [1]:
|
|
(5) |
Полученные формулы справедливы для расчета температур и на многослойной поверхности теплообмена. В этом случае для плоских стенок в формулу (5) подставляется ![]() — полная толщина многослойной стенки и
— полная толщина многослойной стенки и ![]() эквивалентный коэффициент теплопроводности многослойной стенки,
эквивалентный коэффициент теплопроводности многослойной стенки,
|
|
(6) |
Если тепловым сопротивлением стенки можно пренебречь (![]() ), то формула (5) принимает вид:
), то формула (5) принимает вид:
|
|
(7) |
Аналогично, как и для плоской стенки, находится температура горячей поверхности цилиндрической стенки:
|
|
(8) |
где ![]() поверхности, непосредственно соприкасающиеся с теплоносителями,
поверхности, непосредственно соприкасающиеся с теплоносителями, ![]()
Методика исследования построена на использовании параметрического расчетного эксперимента, где целевой функцией является температура горячей стенки (точнее, отношение температуры горячей поверхности стенки к температуре горячего теплоносителя).
С целью обобщения полученных результатов исследование ведется в безразмерных параметрах.
Введем следующие безразмерные параметры:
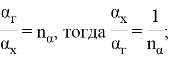
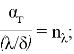
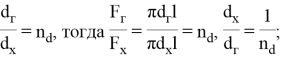
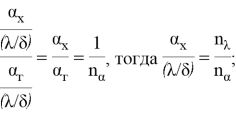
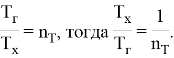
Таким образом, целевая функция в параметрической форме представляется в виде:
а) для плоской стенки
|
|
(9) |
б) для цилиндрической поверхности
|
|
(10) |
Характер исследования — двухпараметрический, т. е. предполагается, что нужно выбрать два из вышеперечисленных параметров, а остальные зафиксировать.
Диапазоны исследования выбраны на основании диапазонов натуральных переменных реальных задач и предстоящих испытаний и составляют:
![]()
![]()
![]()
Расчет и анализ результатов производится по приоритетным параметрам. Результаты эксперимента представляются в графическом виде.
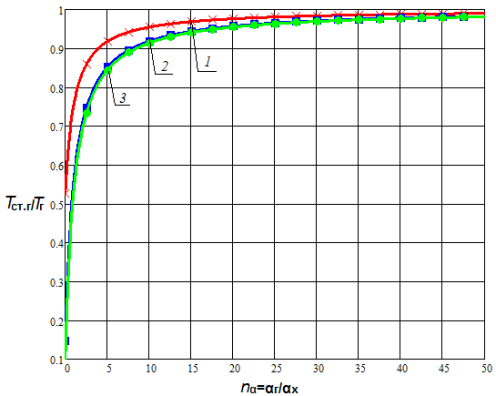
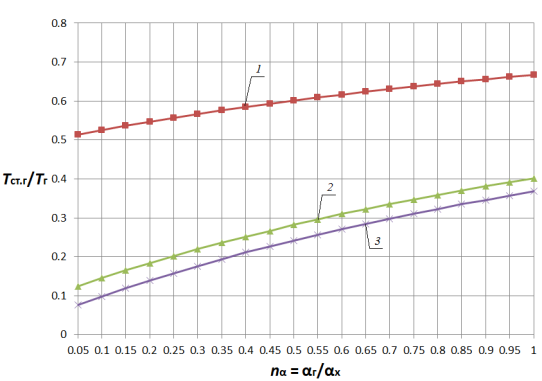
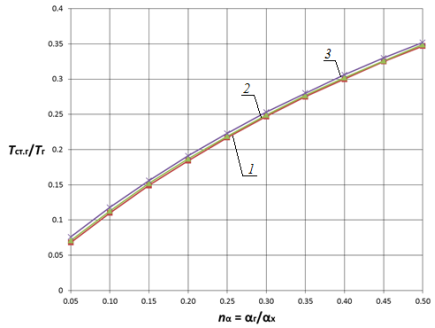
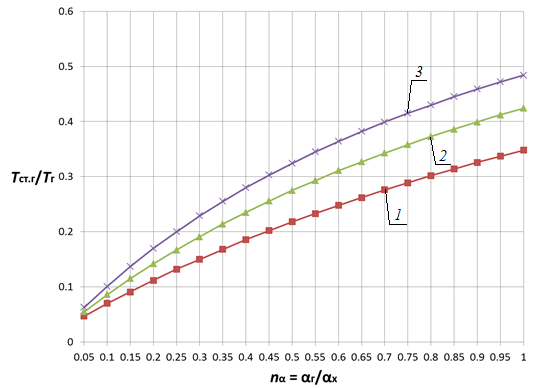
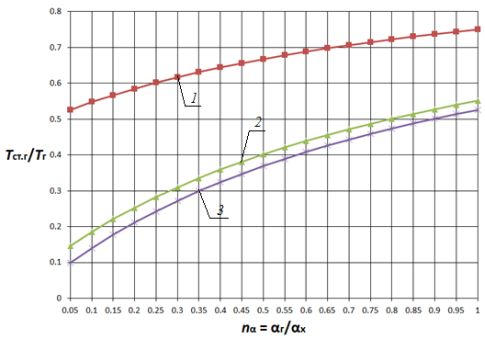
Анализ влияния отношения коэффициентов теплоотдачи показывает, что в диапазоне nα = 0,05…1,0 с увеличением отношения ![]() в 20 раз температура стенки монотонно возрастает приблизительно в 1,4…5,3 раз для плоской стенки и в 1,3…4,6 раз для цилиндрической поверхности теплообмена (рис. 1 (а), рис. 2 (а)) в зависимости от параметров
в 20 раз температура стенки монотонно возрастает приблизительно в 1,4…5,3 раз для плоской стенки и в 1,3…4,6 раз для цилиндрической поверхности теплообмена (рис. 1 (а), рис. 2 (а)) в зависимости от параметров ![]() и
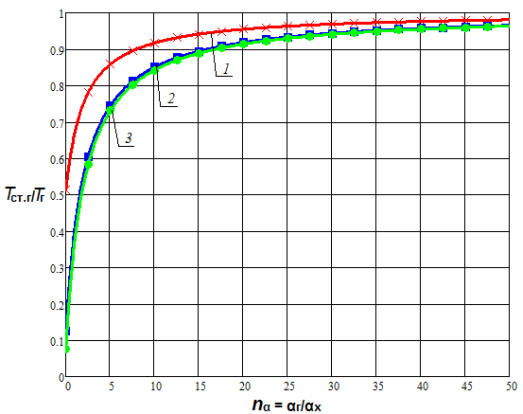
и ![]() при прочих равных условиях. При этом очевидна тенденция снижения этого роста по мере увеличения nα. Увеличение диапазона исследования (рис. 1 (б), рис. 2 (б)) показывает, что наиболее существенное влияние на температуру стенки nα оказывает в диапазоне nα< 5, что существует область значений параметра nα (nα > 15), при которой данный параметр не оказывает существенного влияния на температурное состояние стенки. При этом зависимости температуры плоской и цилиндрической поверхностей теплообмена от одноименных параметров имеют сходственный характер.
при прочих равных условиях. При этом очевидна тенденция снижения этого роста по мере увеличения nα. Увеличение диапазона исследования (рис. 1 (б), рис. 2 (б)) показывает, что наиболее существенное влияние на температуру стенки nα оказывает в диапазоне nα< 5, что существует область значений параметра nα (nα > 15), при которой данный параметр не оказывает существенного влияния на температурное состояние стенки. При этом зависимости температуры плоской и цилиндрической поверхностей теплообмена от одноименных параметров имеют сходственный характер.
|
а) |
|
|
|
б) |
|
Рис. 1. Зависимость Tст.г/Tг от nα и nT при nλ = 0,005 для плоской стенки 1 — Tг/Тх = 2; 2 — Tг/Тх = 10; 3 — Tг/Тх = 20 |
|
|
|
а) |
|
|
|
б) |
|
Рис. 2. Зависимость Tст.г/Tг от nα и nT при nλ = 0,005 и nd = 0,5 для цилиндрической стенки |
|
1 — Tг/Тх = 2; 2 — Tг/Тх = 10; 3 — Tг/Тх = 20 |
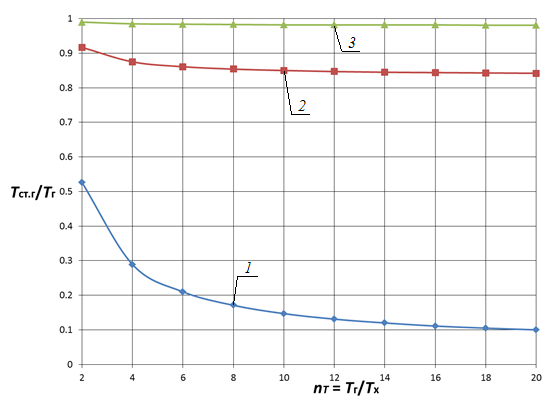
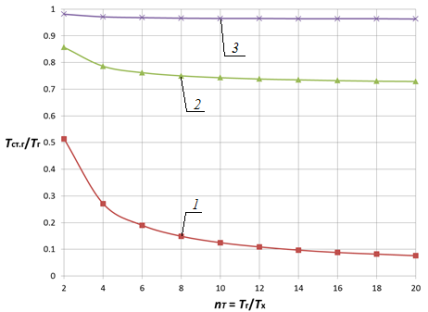
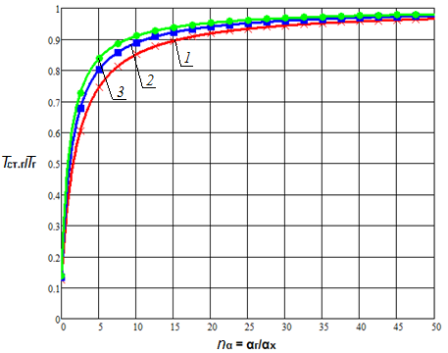
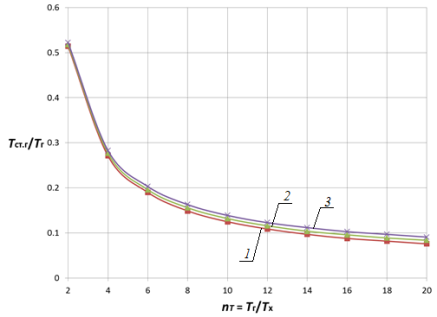
Анализ влияния отношения температур горячего и холодного теплоносителей![]() в исследованном диапазоне показывает следующее. При малых значениях nα увеличение температурного напора
в исследованном диапазоне показывает следующее. При малых значениях nα увеличение температурного напора ![]() ведет к существенному снижению температуры стенки, тогда как при больших значениях параметра (nα > 1) во всем диапазоне
ведет к существенному снижению температуры стенки, тогда как при больших значениях параметра (nα > 1) во всем диапазоне ![]() существенного снижения температуры стенки не наблюдается и ее относительное значение приближается к своему максимуму, т. е. Tст/Tг ≈ 1. Так, с ростом отношения температур горячего и холодного теплоносителей
существенного снижения температуры стенки не наблюдается и ее относительное значение приближается к своему максимуму, т. е. Tст/Tг ≈ 1. Так, с ростом отношения температур горячего и холодного теплоносителей![]() в 10 раз (рис. 3 и 4) температура стенки уменьшается в 5,3…1,1 раза для плоской стенки и в 6,4…1,2 раз для цилиндрической поверхности теплообмена на границах области nα = 0,05…50.
в 10 раз (рис. 3 и 4) температура стенки уменьшается в 5,3…1,1 раза для плоской стенки и в 6,4…1,2 раз для цилиндрической поверхности теплообмена на границах области nα = 0,05…50.
|
|
|
Рис. 3. Зависимость Tст.г/Tг от nT и nα при nλ = 0,005 для плоской стенки 1 — nα = 0,05; 2 — nα = 5; 3 — nα = 50 |
|
|
|
Рис. 4. Зависимость Tст.г/Tг от nT и nα при nλ = 0,005и nd = 0,5 для цилиндрической стенки |
|
1 — nα = 0,05; 2 — nα = 5; 3 — nα = 50 |
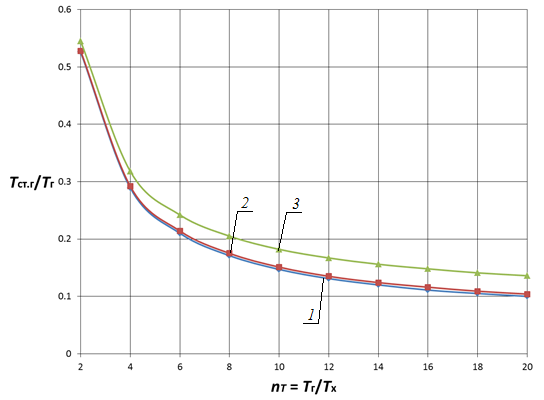
Исследование влияния проводимости стенки ![]() показывает ее слабое (до ничтожного) влияние на температурное состояние стенки в широком диапазоне исследованных параметров nλ, nα, nT (рис. 5–7).
показывает ее слабое (до ничтожного) влияние на температурное состояние стенки в широком диапазоне исследованных параметров nλ, nα, nT (рис. 5–7).
|
|
|
Рис. 5. Зависимость Tст.г/Tг от nα и nλ при nT = 20 для плоской стенки |
|
1 — nλ = 0,001; 2 — nλ = 0,005; 3 — nλ = 0,01 |
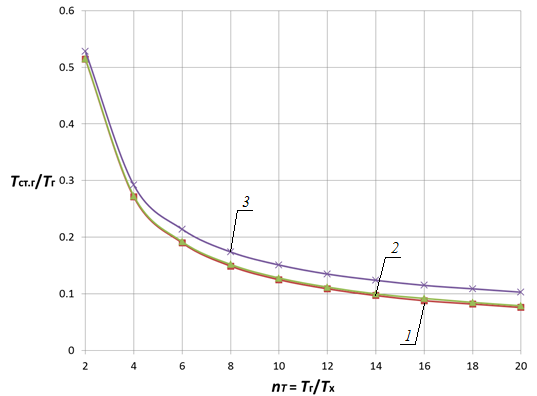
Анализ исследования влияния кривизны ![]() цилиндрической стенки (рис. 8 и 9) показывает следующее. Характер влияния кривизны на температуру стенки подобен влиянию nα и
цилиндрической стенки (рис. 8 и 9) показывает следующее. Характер влияния кривизны на температуру стенки подобен влиянию nα и ![]() . Так с увеличением степени кривизны (уменьшением
. Так с увеличением степени кривизны (уменьшением ![]() ) как и с увеличением
) как и с увеличением ![]() (рис. 1) и уменьшением nα (рис. 3, 4) температура стенки уменьшается. Количественная мера влияния
(рис. 1) и уменьшением nα (рис. 3, 4) температура стенки уменьшается. Количественная мера влияния ![]() на температуру стенки уменьшается с увеличением степени кривизны до 30 % в диапазоне nα = 0,05…1,0, особенно с ростом nα до 1,0, с дальнейшим ростом nα влияние уменьшается до 3…6 %.
на температуру стенки уменьшается с увеличением степени кривизны до 30 % в диапазоне nα = 0,05…1,0, особенно с ростом nα до 1,0, с дальнейшим ростом nα влияние уменьшается до 3…6 %.
|
|
|
Рис. 6. Зависимость Tст.г/Tг от nT и nλ при nα = 0,05 для плоской стенки 1 — nλ = 0,001; 2 — nλ = 0,005; 3 — nλ = 0,01 |
|
|
|
Рис. 7. Зависимость Tст.г/Tг от nT и nλ при nα = 0,05 и nd = 0,5 для цилиндрической стенки |
|
1 — nλ = 0,001; 2 — nλ = 0,005; 3 — nλ = 0,01 |
|
|
|
а) |
|
|
|
б) |
|
Рис. 8. Зависимость Tст.г/Tг от nα и nd при nT = 50 и nλ = 0,005 для цилиндрической стенки 1 — nd = 0,5; 2 — nd = 0,7; 3 — nd = 0,9 |
|
|
|
Рис. 9. Зависимость Tст.г/Tг от nT и nd при nα = 0,05 и nλ = 0,005 для цилиндрической стенки 1 — nd = 0,5; 2 — nd = 0,7; 3 — nd = 0,9 |
На основании полученных результатов сделаны следующие выводы:
1) Наиболее существенное влияние на температуру горячей поверхности стенки оказывают параметры nα и nT в диапазонах: nα < 1,0…5,0 и nT < 10…15.
2) Влияние степени кривизны цилиндрической стенки на температуру стенки значительно менее существенно и составляет по величине от 3 до 30 % в исследованном диапазоне параметров.
3) Влиянием относительной проводимости стенки в исследованном диапазоне параметров можно с достаточной точностью пренебрегать.
Литература:
- В. П. Исаченко, В. А. Осипова. А. С. Сукомел. Теплопередача. Учебник для вузов, Изд. 4-е перераб. и доп. — М.: «Энергоиздат», 1981. — 415 с.