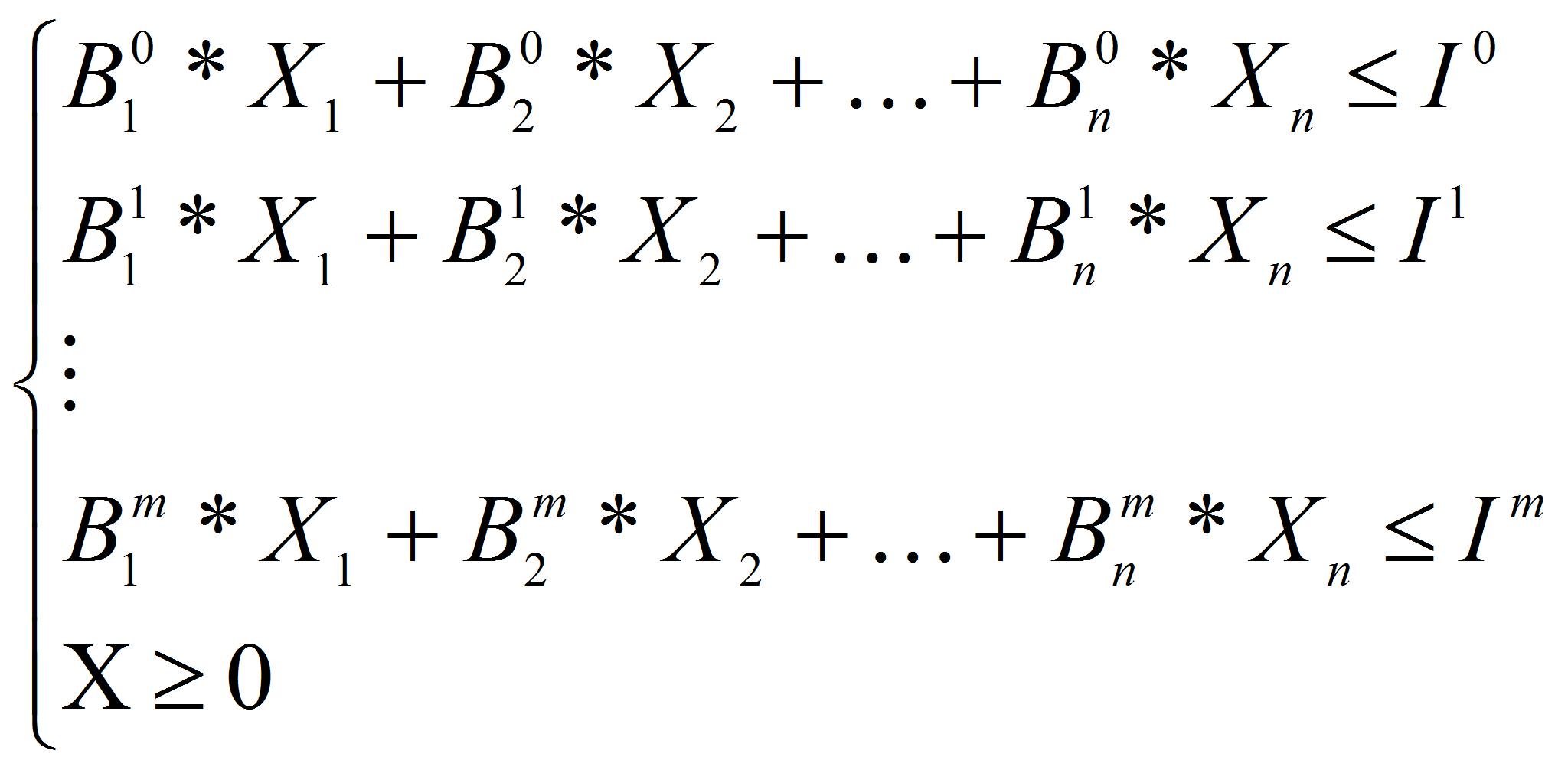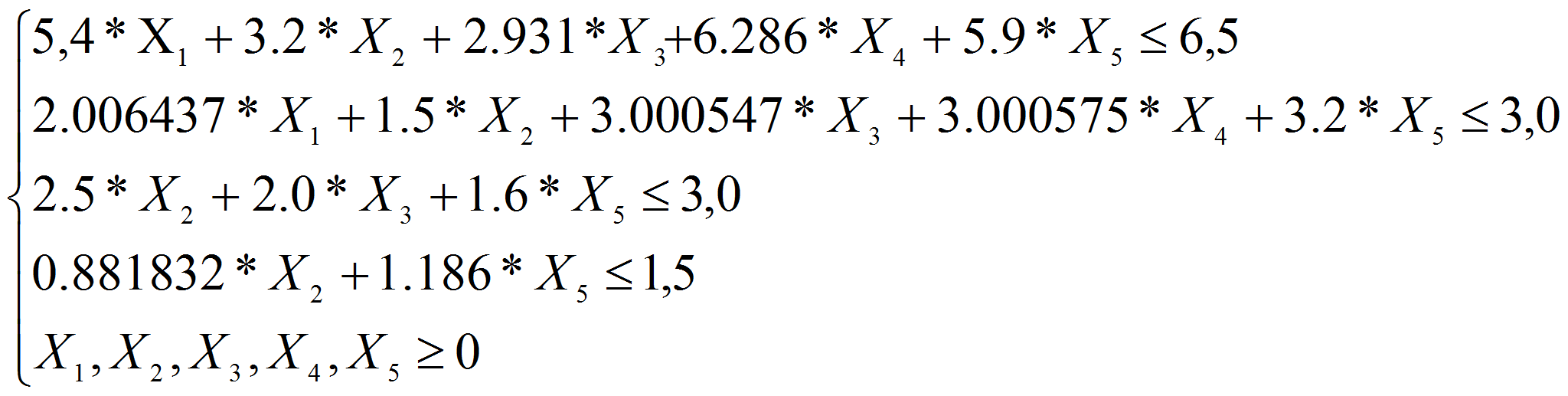The Analysis of Mathematical Model of Information System
Автор: Семахин Андрей Михайлович
Рубрика: 1. Информатика и кибернетика
Опубликовано в
международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2012)
Статья просмотрена: 131 раз
Библиографическое описание:
Семахин, А. М. The Analysis of Mathematical Model of Information System / А. М. Семахин. — Текст : непосредственный // Технические науки: теория и практика : материалы I Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита : Издательство Молодой ученый, 2012. — С. 31-34. — URL: https://moluch.ru/conf/tech/archive/7/2057/ (дата обращения: 27.04.2024).
The modern organization represents complex dynamic system. Perfection of information system is provided with use of modern means, the software and mathematical modeling.
Let's develop mathematical model of information system and we shall lead its analysis.
The mathematical model is formulated as follows: from among the firms, rendering services satellite Internet in territory of the Russian Federation, it is required to choose the provider satellite Internet with the maximal size of the net present value (NPV) and satisfying to financial restrictions.
The mathematical model includes two stages:
1. A method of expert estimations the firms giving satellite Internet in territory of the Russian Federation get out.
2. Methods of mathematical programming the optimum variant from among the satellite providers chosen at the first stage gets out.
Let
![]() - number of variants of projects satellite Internet;
- number of variants of projects satellite Internet;
![]() - number of the experts estimating variants of projects satellite
Internet;
- number of the experts estimating variants of projects satellite
Internet;
![]() -number of factors;
-number of factors;
![]() - the weight appropriated q by the expert k to the factor,
- the weight appropriated q by the expert k to the factor,
![]() -an estimation given q by the expert k to the factor then the average
estimation of i variant of the project satellite Internet is defined
under the formula
-an estimation given q by the expert k to the factor then the average
estimation of i variant of the project satellite Internet is defined
under the formula
At the second stage the optimum project from among the projects certain at the first stage gets out. The problem of linear programming of a choice of the optimum project from an investment portfolio is formulated.
The mathematical model of a choice of the optimum investment project satellite Internet looks like:
under restrictions
where
![]() is a target parameter, unit of measurement;
is a target parameter, unit of measurement;
![]() is investment expenses of i project in j period of
time, million. roubles;
is investment expenses of i project in j period of
time, million. roubles;
![]() is available means of financing in j period of
time, million. roubles;
is available means of financing in j period of
time, million. roubles;
![]() is a share of financing of the investment project;
is a share of financing of the investment project;
![]() is a number of the investment project;
is a number of the investment project;
![]() is a number of the period of time, year.
is a number of the period of time, year.
Let's carry out a choice of the optimum project satellite Internet for the District Compulsory Medical Insurance Fund of Kurgan region and we shall lead its analysis.
As a result of the first stage in a portfolio of investments are included by Joint-Stock Company " NTV-plus " (199 points), Europe Online Networks (EOL) (177 points), Astra Networks (157 points), Satpro (152 points) and Network Service (137 points).
Let's execute the second stage of mathematical model.
Let
![]() - a share of financing of the project NTV-plus,
- a share of financing of the project NTV-plus,
![]() - a share of financing of project Europe On Line,
- a share of financing of project Europe On Line,
![]() - a share of financing of project Astra Network,
- a share of financing of project Astra Network,
![]() - a share of financing of project Satpro,
- a share of financing of project Satpro,
![]() - a share of financing of project Network Service.
- a share of financing of project Network Service.
The mathematical model looks like
under restrictions (3)
The linear programming task is solved by Gauss – Jordan’s method [1, p. 107].
The optimum decision of a problem is resulted in table 1.
Let's lead the analysis of mathematical model.
Economic sense of additional variables
![]() - size of not used means of financing. Values of variables
- size of not used means of financing. Values of variables
![]() ,
,
![]() ,
hence, are completely used means of financing during periods
,
hence, are completely used means of financing during periods
![]() Values of variables
Values of variables
![]() and
and
![]() ,
hence, means of financing during periods
,
hence, means of financing during periods
![]() are underused on 2,3881 and 1,5 million
roubles.
are underused on 2,3881 and 1,5 million
roubles.
The dual estimation of required variables
![]() shows presence/absence of financing i project. If the dual estimation
is equal 0 financing of the project is made. If the dual estimation
of variable
shows presence/absence of financing i project. If the dual estimation
is equal 0 financing of the project is made. If the dual estimation
of variable
![]() is strictly positive, financing is not carried out. Dual estimations
is strictly positive, financing is not carried out. Dual estimations
![]() and
and
![]() have zero values, projects of NTV-plus and Astra Network are
financed. Dual estimations
have zero values, projects of NTV-plus and Astra Network are
financed. Dual estimations
![]() ,
,
![]() and
and
![]() are equal 0,2526, 1,8225 and 1,4259. Projects Europe On Line, Satpro
and Network Service are not financed.
are equal 0,2526, 1,8225 and 1,4259. Projects Europe On Line, Satpro
and Network Service are not financed.
Table 1
The optimum decision of a problem
|
Variable |
Size of variables |
Dual estimation |
Extremum of criterion function NPV, million roubles. |
|
1,0376 |
0,0000 |
2,00526 |
|
|
0,0000 |
0,2526 |
||
|
0,3060 |
0,0000 |
||
|
0,0000 |
1,8225 |
||
|
0,0000 |
1,4259 |
||
|
0,0000 |
0,1768 |
||
|
0,0000 |
0,2853 |
||
|
2,3881 |
0,0000 |
||
|
1,5000 |
0,0000 |
The dual estimation of variable
![]() defines deficiency of a resource. It shows on how many will increase
NPV at increase j a resource for one unit. Dual estimations of
variables
defines deficiency of a resource. It shows on how many will increase
NPV at increase j a resource for one unit. Dual estimations of
variables
![]() and
and
![]() are equal 0,1768 and 0,2853. It means that at increase in the
allocated means of financing at 1 million roubles during periods
are equal 0,1768 and 0,2853. It means that at increase in the
allocated means of financing at 1 million roubles during periods
![]() NPV will increase on 0,1768 and 0,2853 million roubles. During
periods
NPV will increase on 0,1768 and 0,2853 million roubles. During
periods
![]() the increase in means of financing is not recommended (dual
estimations of variables
the increase in means of financing is not recommended (dual
estimations of variables
![]() and
and
![]() have zero values).
have zero values).
The analysis of stability of the optimum decision is resulted in change of factors of criterion function in table 2.
The bottom border of an interval of the stability,
equal -![]() ,
corresponds to zero value of a required variable. If value of factor
of criterion function changes within the limits of an interval of
stability from bottom up to the top border value of criterion
function changes. In case of an output abroad an interval of
stability the size of criterion function and value of required
variables varies [2, p. 20].
,
corresponds to zero value of a required variable. If value of factor
of criterion function changes within the limits of an interval of
stability from bottom up to the top border value of criterion
function changes. In case of an output abroad an interval of
stability the size of criterion function and value of required
variables varies [2, p. 20].
Table 2
Factors of criterion function of mathematical model
|
Number of the subitem
|
The minimal value of factor |
Reference value of factor |
The maximal value factor |
|
|
1 |
1,0265 |
1,5273 |
2,5321 |
|
|
2 |
0,7412 |
0,9938 |
||
|
3 |
0,8290 |
1,3744 |
2,2840 |
|
|
4 |
0,1451 |
1,9676 |
||
|
5 |
0,5303 |
1,9562 |
If variable
![]() accepts nonzero value in the optimum plan (
accepts nonzero value in the optimum plan (![]() ,
,![]() ) the factor at this variable (investment expenses i the project,
) the factor at this variable (investment expenses i the project,
![]() , j the period of time
, j the period of time
![]() ), changing within the limits of an interval of stability, will lead
to change of criterion function, and distribution add financings it
will be kept. If the size of factor at variable
), changing within the limits of an interval of stability, will lead
to change of criterion function, and distribution add financings it
will be kept. If the size of factor at variable
![]() leaves for the top border of an interval of stability the share of
financing j the project will increase due to shares of financing of
other projects. Otherwise the share of financing j the project will
be reduced, and shares of financing of other projects will increase.
leaves for the top border of an interval of stability the share of
financing j the project will increase due to shares of financing of
other projects. Otherwise the share of financing j the project will
be reduced, and shares of financing of other projects will increase.
If variable
![]() accepts zero value in case of change of factor of a variable inside
of an interval of stability in the decision of a problem nothing will
change. If the size of factor will leave for the top border of an
interval of stability the given project is necessary to start for
financing, reducing financing of other projects. For example,
investment projects Europe On Line, Satpro and Network Service in the
optimum decision have zero values of required variables (there is no
financing). If NPV project Satpro will exceed 1,9676 million roubles
the project will start to be financed. Similarly for projects Europe
On Line and Network Service.
accepts zero value in case of change of factor of a variable inside
of an interval of stability in the decision of a problem nothing will
change. If the size of factor will leave for the top border of an
interval of stability the given project is necessary to start for
financing, reducing financing of other projects. For example,
investment projects Europe On Line, Satpro and Network Service in the
optimum decision have zero values of required variables (there is no
financing). If NPV project Satpro will exceed 1,9676 million roubles
the project will start to be financed. Similarly for projects Europe
On Line and Network Service.
The analysis of stability of the optimum decision is resulted in change of the right parts of restrictions in the table. 3.
Table 3
Values of the right parts of system of restrictions
|
Number of the subitem
|
The period of time f |
The minimal value of the right part of restrictions |
Reference value of the right part of restrictions |
The maximal value of the right part of restrictions |
|
1 |
0 |
2,9305 |
6,5 |
8,0740 |
|
2 |
1 |
2,4152 |
3,0 |
5,2824 |
|
3 |
2 |
0,6119 |
3,0 |
|
|
4 |
3 |
0,0 |
1,5 |
In the optimum plan of means of
financing are underused in the periods of time
![]() and
and
![]() ,
because the top border of an interval of stability +
,
because the top border of an interval of stability +![]() .
If available means of financing it is a lot of, change in an interval
of stability does not change the list of financed projects, shares of
financing and size NPV. At an output for the bottom border of an
interval of stability shares of financing and size NPV vary the list
of financed projects. For example, if means of financing of projects
in the period of time
.
If available means of financing it is a lot of, change in an interval
of stability does not change the list of financed projects, shares of
financing and size NPV. At an output for the bottom border of an
interval of stability shares of financing and size NPV vary the list
of financed projects. For example, if means of financing of projects
in the period of time
![]() will be less than 0,6119 million roubles the list of financed
projects will change, shares of financing and size NPV. If means of
financing are spent completely its change in an interval of stability
does not change the list of financed projects, but changes a share of
financing and size NPV. At an output abroad an interval of stability
the list of financed projects, shares of financing and sizes NPV
varies. For example, if means of financing in the period of time
will be less than 0,6119 million roubles the list of financed
projects will change, shares of financing and size NPV. If means of
financing are spent completely its change in an interval of stability
does not change the list of financed projects, but changes a share of
financing and size NPV. At an output abroad an interval of stability
the list of financed projects, shares of financing and sizes NPV
varies. For example, if means of financing in the period of time
![]() will change from 2,9305 million roubles up to 8,0740 million roubles
financing of projects will not change (NTV Plus and Astra Network
with values
will change from 2,9305 million roubles up to 8,0740 million roubles
financing of projects will not change (NTV Plus and Astra Network
with values
![]() and
and
![]() ),
but will change shares of financing and size NPV. If means of
financing overstep the bounds of an interval the list of financed
projects will change, share of financing and size NPV.
),
but will change shares of financing and size NPV. If means of
financing overstep the bounds of an interval the list of financed
projects will change, share of financing and size NPV.
Results of the lead researches have allowed to draw following conclusions.
1. The mathematical model of optimization of the information systems is developed, allowing to reduce expenses and terms of designing of information systems and to raise validity of accepted decisions.
2. The analysis of variables and mathematical model on stability of factors of criterion function and values of the right parts of restrictions is lead.
References:
H. A. Taha. Operations Research: An Introduction. Seven Edition: Traslation From English, M.: Publishing House Williams, 2005. – 912 p.
Kochkina E.M., Radkovskaya E.V. Methods Of Research And Modelling Of National Economy. - Ekaterinburg, Publishing house Ural State Economic University, 2001. - 93 p.