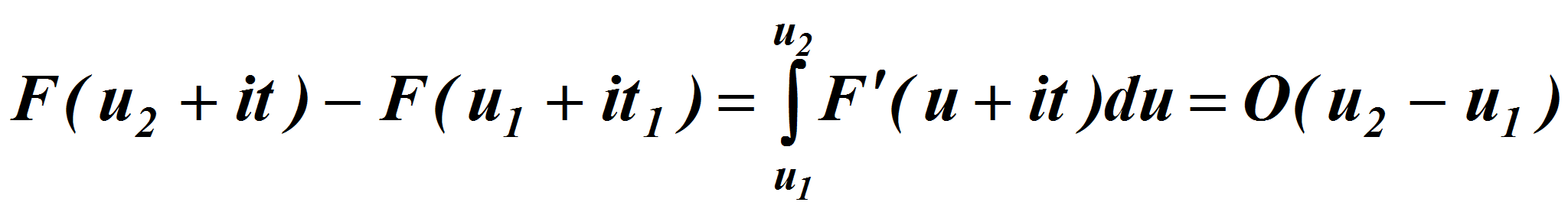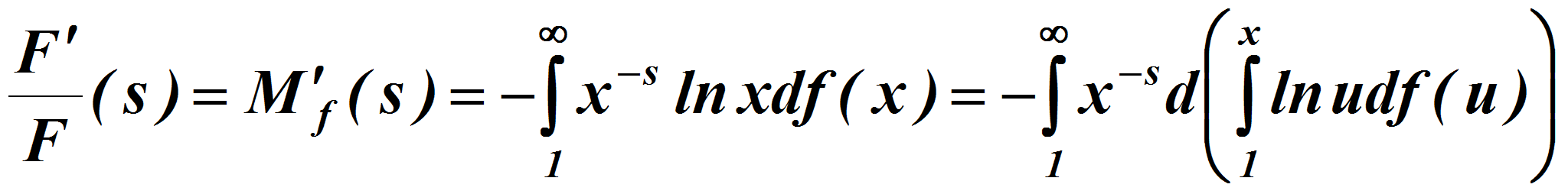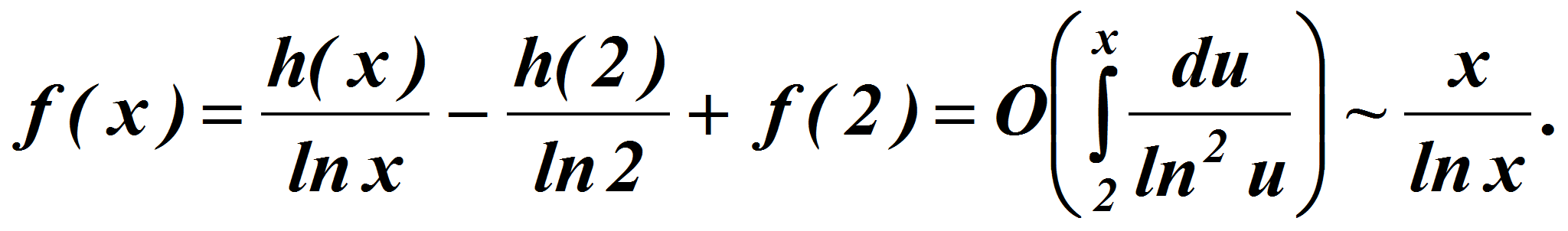Работа содержит достаточные условия, которым должно удовлетворять преобразование Меллина неубывающей функции , чтобы была справедлива асимптотическая формула при . Из полученных результатов, в частности, при здесь содержится асимптотический закон распределения простых чисел.

Work contains sufficient conditions with which should satisfy transformation Меllin of not decreasing function that it was fair Asymptotic formulae at . From the received results, in particular, at here contains asymptotic the law of distribution of simple numbers.

Пусть − неубывающая функция, определенная при

Поставим вопрос о том, какие минимальные ограничения на функцию обеспечивают асимптотическую формулу

− аналог закона простых чисел.

В работе доказывается следующая лемма.

Лемма 1. Пусть интеграл сходится при ,. Если производная равномерно продолжима на прямую , исключая точку ,

при , то функция не обращается в нуль в замкнутой полуплоскости .

Мы воспользовались тем, что из равномерной продолжимости следует равномерная продолжимость , так как при

,

что влечет за собой равномерную продолжимость функции , и следовательно, оценку

Далее из равенства следует

.

Функция очевидно неубывающая.

Применим к ней сформулированную ниже теорему Икеара.

Теорема. (Теорема Икеара [2]). Пусть неубывающая функция, определенная при .

Если функция

равномерно продолжима на прямую , то при .

В нашем случае

,

так что из предыдущего вытекает, что условия теоремы Икеара выполнены. Согласно этой теоремы

Отсюда следует

,

откуда

Теорема доказана.

Литература:

1. Ингам А.Е. Распределение простых чисел.− ОНТИ, 1936.
2. Райков Д.А. Обобщение теоремы Икеара−Ландау.− Матем. сб. 8(45), №3, 1938, 559-568.
3. Постников А.Г. Упрощение элементарного доказательства А.Сельберга асимптотического закона распределения простых чисел.− УМН, т.х., 1955, №4.