Применение многоуровневой фрактальной модели для задач тематической обработки данных



Рассмотрено применение метода покрытий многоуровневой фрактальной модели при анализе текстур изображений для задач тематической обработки данных, при этом выявлено, что оценка фрактальной размерности определяется наклоном, порождаемым первым и последним масштабами, в то время как промежуточные масштабы не дают вклада в расчеты. Определено, что метод имеет морфологическое осуществление и дает возможность использовать расчетные преимущества морфологической обработки данных, при этом предложенный метод определен в рекурсивной форме и позволяет вести расчеты при больших массивах данных.

Ключевые слова: локальная фрактальная размерность, морфологическое расширение, фрактальная размерность, рекурсивная форма метода, фрактальная сигнатура, морфологическое разрушение, сероуровневая поверхность.

При решении задач тематической обработки данных часто приходится анализировать пространственную структуру поля интенсивности изображений. Для детальных изображений характерно наличие целей и стохастического фона. Для текстурных изображений с точки зрения информативности необходимо учитывать параметры всего изображения. Практически в любых изображениях земных покровов можно выделить области, относящиеся к текстурным изображениям [1]. В последние годы для анализа природных объектов все чаще используются методы фрактальной геометрии. Универсальное описание естественных и антропогенных объектов в оптическом диапазоне представлено в [2], где фрактальная размерность рассчитывается как фрактальная сигнатура для различения поверхностных неровностей.

Фрактальные сигнатуры, полученные с помощью морфологического фильтра, использованы для идентификации ландшафтов и объектов военной техники на фоне земных покровов. Оценка фрактальной размерности проводилась модифицированным методом покрытий, разработанным для анализа текстурных изображений [3]. Рассмотрим метод покрытий в анализе текстур. Суть данного метода состоит в том, что квантованные значения интенсивности двумерного сигнала должны располагаться между двумя функциями, называемыми верхней и нижней поверхностями. Верхняя поверхность содержит множество точек, значения которых всегда, по крайней мере, на один квант превышают интенсивность входного сигнала. Нижняя поверхность L имеет значения точек, которые всегда ниже, по крайней мере, на один квант интенсивности входного изображения.

Верхняя и нижняя поверхности при нулевой шкале масштабов определяются как

(1)

где g(i, j) ‒ входное изображение. В общем случае

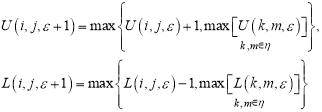(2)

где η = {(k, m)} расстояние { [(k, m), (i, j)] ≤ 1}.

Сконструированное покрытие, образованное двумя указанными функциями, имеет толщину 2ε. Для двумерного сигнала площадь «поверхности» есть объем, занятый покрытием и деленный на величину 2ε. Площадь «поверхности» интенсивности А(ε) в пределах окна наблюдения R рассчитывают вычитанием точки за точкой нижней «поверхности» из верхней с дальнейшим суммированием по всему окну [1].

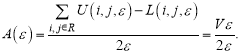(3)

Фрактальную размерность определяют по наклону log А(ε) как функцию log ε. В [3] измеряемая «поверхность» А₁(ε) определяется разностью объемов при последовательных масштабах:

(4)

На основе (9.40) получаем

(5)

Тогда из [3] имеем

(6)

где К ‒ постоянная величина.

Рассчитанное значение А₁(ε) является аппроксимацией производной V(ε) по ε и определяется по формуле

(7)

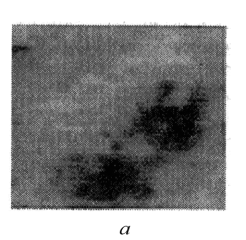
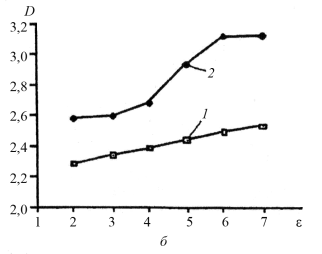
Рис. 1. Изображение дерева (а) и фрактальные сигнатуры (б), определенные по формуле (3) — кривая 1 и (4) — кривая 2

Следует уточнить, что реальные изображения всегда имеют шумовую составляющую, поэтому расчет А(ε) по (7) может дать оценку шума. В качестве примера на рис. 1,а приведено изображение размером 32х32 пиксел дерева, а на рис. 1,б ‒ соответствующие фрактальные сигнатуры, рассчитанные по формулам (3) и (4). Значения D соответствующие (3), находятся в ожидаемом диапазоне от 2 до 3 при котором D = 2 соответствует плоской поверхности. Фрактальная сигнатура, рассчитанная по (4), превышает допустимую верхнюю границу, равную 3. Следовательно, расчет по производной дает сильную шумовую составляющую. Фрактальная размерность D(i, j) при нахождении пиксела (i, j) на всех масштабах оценивается в [4] как взвешенная сумма локальных фрактальных размерностей F(i, j) в виде

(8)

при

(9)

Вследствие свойства масштабирования фракталов величина F_ε(i, j) является результатом деления A(i, j, ε) на A(i, j, ε — 1):

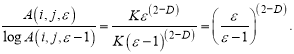(10)

Логарифмируя (10), имеем

(11)

Локальные фрактальные размерности F_ε(i, j) рассчитывают только на промежуточных этапах. Затем последовательные значения F_ε(i, j) накапливаются с определенными весами по всему диапазону шкал для получения оценки фрактальной размерности D(i, j). Соотношение (8) является функцией только первой и последней шкал масштабов. Элемент суммы числителя в (8)

Тогда

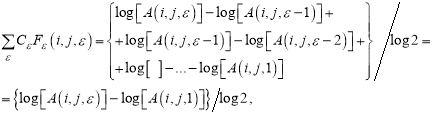(12)

при этом

Уравнение (12) показывает, что оценка фрактальной размерности определяется наклоном, порождаемым первым и последним масштабами, в то время как промежуточные масштабы не дают вклада в расчеты.

Рассмотрим морфологическое осуществление метода. Предложенный метод покрытий для нахождения D прост и одновременно эффективен в реализации. Следует уточнить, что метод определен в рекурсивной форме, позволяющей вести расчеты при больших массивах данных. Соответственно метод имеет морфологическое осуществление, что дает возможность использовать расчетные преимущества морфологической обработки. Расчеты верхней и нижней поверхностей по (2) эквивалентны морфологическому расширению и разрушению [5]. Данные операции определяются как:

разрушение:

расширение:

здесь (k) ‒ двумерные фигуры, размер, форма и пространственная ориентация которых определяют фильтрующие свойства; Ros(k) ‒ область содержания k. Данные о выходной точке получаются расположением ядра k на определенной доле входного образа и действием min-оператором (при разрушении) или mах-оператором (при расширении) на значения, объемлемые ядром. Такая операция повторяется при перемещении ядра по всему образу g.

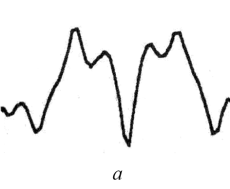
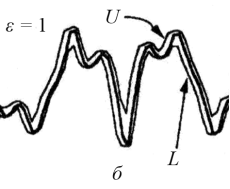
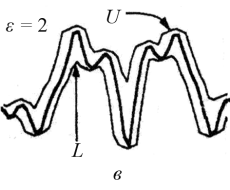
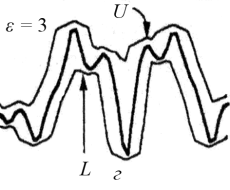
Рис. 2. Конструирование верхней U и нижней L «поверхностей» при различных масштабах: а ‒ истинный одномерный сигнал; б ‒ масштаб ε = 1; в ‒ ε = 2; г ‒ ε = 3

Разнообразие функциональных морфологических операций достигается использованием этих простейших действий. На рис.2 представлено создание верхней U и нижней L «поверхностей» при различных масштабах. Можно считать, что изображения являются комбинацией различных сероуровневых «поверхностей», которые самоподобны в определенном диапазоне масштабов и поэтому их соответствующие фрактальные размерности стабильны на малом числе шкал. Схема расчета фрактальной сигнатуры по формуле (3) морфологическим фильтром приведена в [2] и в [6].

Каждая точка изображения (k, l) определяется оценкой площади при масштабе ε. Для начальной нулевой шкалы верхние и нижние «поверхности» идентичны и равны истинному изображению (см. (1)). Для конечного числа масштабов оценка А(k, l, ε) следует из соотношения

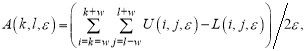(13)

где окно размером (2w+1) x (2w+1) имеет переменные размеры, устанавливаемые нижней и верхней шкалами масштабов.

Предложенный метод покрытий для нахождения D прост и одновременно эффективен в реализации. Следует уточнить, что метод определен в рекурсивной форме, позволяющей вести расчеты при больших массивах данных. Соответственно метод имеет морфологическое осуществление, что дает возможность использовать расчетные преимущества морфологической обработки [8]. Расчеты верхней и нижней поверхностей эквивалентны морфологическому расширению и разрушению. Отметим, что изображения являются комбинацией различных сероуровневых «поверхностей», которые самоподобны в определенном диапазоне масштабов и поэтому их соответствующие фрактальные размерности стабильны на малом числе шкал. Таким образом, для построения многоуровневой фрактальной модели при задачах тематической обработки данных для соответствующей характеристики объектов предложено использовать метод покрытий.

Литература:

1. Потапов А. А. Фракталы в радиофизике и радиолокации: Топология выборки. Изд.2-е, перераб.и доп. М. Университетская книга. 2005. С.848.
2. Peli O. Multiscale Fractal Theory and Object Characterization// Opt. Soc. Am. A. 1990. V. 7. P. 1101–1112.
3. Peleg S., Naor J., Hartely R., Avnir D. Multiple Resolution Texture Analysis and Classification//IEEE Trans. 1984. V. PAMI-6. P. 518–523.
4. Carlotto M. Stein M. C. Detecting Man-Made Change in Imagery// Proc. Soc. Photo-Optical Instruments Engineering. 1985. V. 1002. P. 6–11.
5. Serra J. Image Analysis and Mathematical Morphology. — L.: Academic Press. 1982.
6. Потапов А. А. Фракталы в дистанционном зондирование/Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2000. № 6. С. 3–65.
7. Аветисов А. С., Карпов М. А., Юрков М. В., Егорова Е. В., Нефедов В. И., Харитонов А. Ю. Математическое и программное обеспечение фрактального распознавания природных и искусственных объектов. Электромагнитные волны и электронные системы. № 8. Т.17. 2012. С. 45–48.
8. Аксяитов М. Х., Егорова Е. В., Мартынов Н. В., Рыбаков А. Н. Обнаружение малоконтрастных целей, Успехи современной радиоэлектроники № 1, 2017, стр. 23–26