Методы оптимизации дальности полета летательного аппарата
Автор: Нечепуренко Константин Юрьевич
Рубрика: 7. Технические науки
Опубликовано в
XLII международная научная конференция «Исследования молодых ученых» (Казань, июль 2022)
Дата публикации: 02.07.2022
Статья просмотрена: 47 раз
Библиографическое описание:
Нечепуренко, К. Ю. Методы оптимизации дальности полета летательного аппарата / К. Ю. Нечепуренко. — Текст : непосредственный // Исследования молодых ученых : материалы XLII Междунар. науч. конф. (г. Казань, июль 2022 г.). — Казань : Молодой ученый, 2022. — С. 11-19. — URL: https://moluch.ru/conf/stud/archive/454/17368/ (дата обращения: 27.04.2024).
В статье сформулирована задача оптимизации дальности полета летательного аппарата, рассмотрены классы методов оптимизации и выбраны пригодные для решения поставленной задачи. Рассмотрены алгоритмы выбранных методов.
Ключевые слова: оптимальное управление, оптимизация, дальность полета, методы оптимизации, летательный аппарат.
В настоящее время одним из актуальных направлений инженерной деятельности является улучшение параметров летательных аппаратов (ЛА). Одной из основных характеристик для всех типов ЛА является дальность полета, соответственно, актуальной является задача по ее увеличению. Этого можно достигнуть различными способами для разных типов ЛА. В данной статье предлагается к рассмотрению задача оптимизации дальности полета крылатого летательного аппарата, оборудованного двигательной установкой.
«Оптимизация — процесс нахождения экстремума (глобального максимума или минимума) определённой функции или выбора наилучшего (оптимального) варианта из множества возможных» [1 с.21].
В динамических задачах (где ограничения переменных, зависимы от времени) применяют методы оптимального управления и динамического программирования. Можно использовать эти методы, если произведена постановка задачи:
— задан набор переменных;
— задана область их изменения (наложены ограничения);
— определён вид целевой функции (функции, для которой идет поиск экстремума) от переменных: задан критерий оценки степени достижения поставленной цели.
Общая задача оптимизации управления может быть сформулирована как задача минимизации функционала
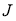
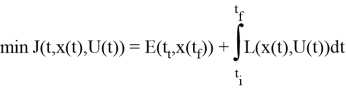
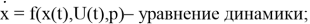
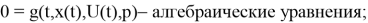
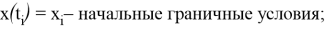
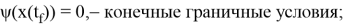
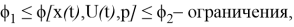
где
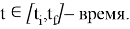
Важно отметить, что начальное время
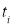
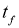
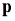
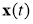
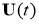
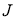
Полагаясь на поставленную задачу оптимизации и математическую модель объекта прежде всего выбирается математический метод, приводящий к результатам с наименьшим потреблением вычислительных ресурсов или же представляющий наибольший объем информации о решении.
К наиболее значимым для решения задачи параметрам относят:
— количество переменных;
— ограничения на переменные процесса;
— математическое описание процесса.
С учетом особенностей объекта (летательного аппарата) можно выделить несколько подходов, применимых для решения задачи оптимизации: методы динамического программирования, прямые и косвенные методы.
Динамическое программирование — метод, применяемый для решения задач оптимизации для задач с дискретизацией по времени, либо имеющих несколько стадий (многостадийных).
Критерий оптимальности задается как аддитивная функция критериев оптимальности отдельных стадий. Если критерий оптимальности имеет иную форме, данный метод также можно применять, но размерность отдельных стадий может увеличиться.
Переменные состояния x (i) и управляющих воздействий u (i) в неидеальных процессах имеют ограничения, определяющие диапазон их изменения или связь между ними. В следствие этого появляются дополнительные условия, выраженные через неравенства или равенства, которые тоже должны входить в систему уравнений, описывающих процесс:
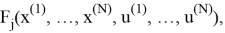
Эффективность одной стадии определяется функцией переменных состояния x (i-1) на i-й стадии и управления на данной стадии u (i) .
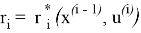
Критерий оптимальности многостадийного процесса тогда определяется как сумма аддитивных функций для каждой стадии процесса:
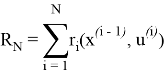
Таким образом, критерий оптимальности определяется совокупностью управляющих воздействий u (i) N , то есть набором векторов u (i) для каждой стадии:
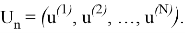
Тогда задача оптимизации многостадийного процесса сводится к оптимизации стратегии управления на всех отдельных стадиях:
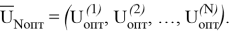
Критерий оптимальности принимает в принимает максимальное или минимальное значение в зависимости от целей задачи оптимизации.
Метод динамического программирования основан на принципе оптимальности:
Вне зависимости от начального состояния x
(0)
и управления на первой стадии u
(1)
, управления на всех последующих стадиях u
(i)
(i
Исходя из этого, оптимальное управление на последующих стадиях определяется только состоянием выхода первой стадии:
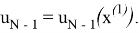
Если известна оптимальная стратегия управления u N -1 , то можно получить оптимальное управление первой стадии
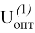
Таким образом, оптимизацию многостадийного процесса начинают с последней стадии, так как для нее не существует последующих стадий, влияющих на выбор управления
u
опт
(N)
на этой стадии. После нахождения оптимального управления
u
опт
(N)
для всех возможных состояний входа последней стадии
x
(N-
1
)
Прямые методы состоят в дискретизации непрерывной задачи оптимального управления и построении последовательности точек управления.
Одним из наиболее распространенных является метод проекции градиента.
Сначала выбирается некоторая точка х [0] из допустимой области G. Уравнения для градиентного метода будут выглядеть следующим образом:
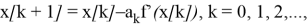
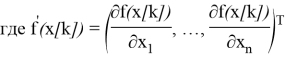
градиент целевой функции f(х) в точке x [ k ].
В некоторой граничной точке
х
[
k
]
, k
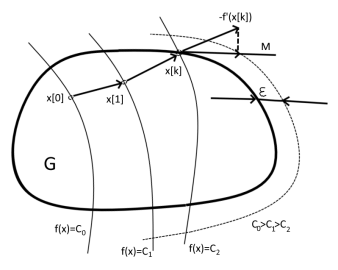
Рис. 1. Геометрическая интерпретация метода проекции градиента
Активными называют ограничения-неравенства если они в точке x [k] превращаются в равенства:
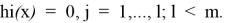
Обозначим через J набор индексов j(1≤j≤
l
) этих ограничений. Их уравнения определяют гиперповерхности, образующие нелинейную (в общем случае) границу области G в окрестности точки х [k]. Ограничения hj(x), j
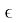
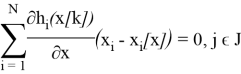
Полученные гиперплоскости ограничивают некоторый многогранник М, аппроксимирующий допустимую область G в окрестности точки х [k] (см. Рис. 1).
Проекция р [k] вектора -f'(x [k]) на многогранник:
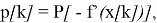
где Р — оператор ортогонального проектирования, заданный выражением
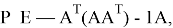
где Е — единичная матрица размеров n; А — матрица размеров l х n. Она образуется транспонированными векторами-градиентами а j , j=1,..., i, активных ограничений. Далее осуществляется спуск в выбранном направлении:
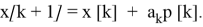
Можно показать, что точка х [ k +1] является решением задачи минимизации функции f(х) в области G тогда и только тогда, когда
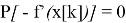
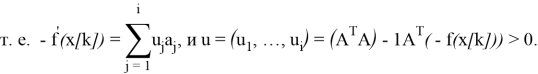
В общем виде алгоритм метода проекции градиента можно представить в виде нескольких этапов:
— Поиск направления спуска p [k] в выбранной точке x [k];
— Определение величины шага а k ;
— Определяется новое приближение х [k+1].
1. Поиск направления спуска. В качестве начального приближения выбирается точка
х
[
k
]
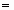
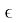
А) Если Р [-f’(х [k])] не равна 0. За направление спуска р [k] принимают полученную проекцию;
Б)
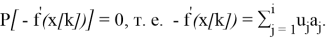
Это выражение является системой из
п
уравнений для определения коэффициентов
и
j
. При условии
и
j
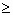
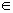
2. Для определения величины шага
а
k
вводится дополнительный параметр точности соблюдения ограничений (положительное число b). Целевая функция минимизируется по направлению
р
[
k
] при условии с соблюдением ограничений. Точка
х
удовлетворяет условиям задачи с заданной точностью, если
h
i
(х)
≤b
, j
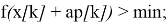
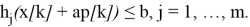
3. Определение нового приближения начинается с вычисления следующей точки:
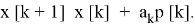
Если векторы р [k] стремятся к 0, то процесс сходится.
Недостатком рассмотренного метода является медленная сходимость.
Косвенные методы используют вариационное исчисление и принцип максимума Понтрягина.
В некоторых задачах оптимизации удобно использовать принцип максимума. Тогда решение может быть представлено в виде разрывных функций, что характерно для подобного класса задач.
Среди косвенных методов наиболее распространен метод последовательных приближений. Рассмотрим его принцип.
Объект управления описывается уравнениями с начальными условиями и ограничениями:
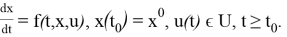
Необходимо определить допустимое управление u(t), минимизирующее функционал
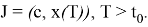
Если поставленная задача имеет решение в классе допустимых уравнений u(t), это решение будет являться оптимальным управлением.
Введем n-мерный вектор p=(p1, …, pn) сопряженных переменных (импульсов), функцию Гамильтона H и запишем сопряженную систему и условия трансверсальности
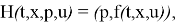
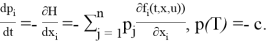
Согласно принципу максимума [2, с.251], искомое оптимальное управление доставляет функции H из (1) максимум по u
В качестве начального приближения u (1) (t) зададим некоторое допустимое управление; при его выборе обычно используются различные физические соображения. Метод состоит из последовательных итераций; k-я итерация заключается в следующем (k=1, 2, …):
— Решая задачу Коши (1) с управлением u=u ( k ) (t), определяем траекторию. x=x ( k ) (t) на интервале [t 0 , T];
— Решая задачу Коши (2) «справа налево» от момента t=T до t=t 0 при u=u ( k ) (t), x=x ( k ) (t), определяем сопряженные переменные p ( k ) (t) на интервале [t 0 , T];
— Определяем управление u=u ( k +1) (t) на интервале [t 0 , T] из условия
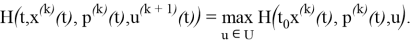
Далее осуществляется переход к следующей итерации и т. д.
При сходимости процесса последовательных приближений, процесс оптимизации продолжается до тех пор, пока результаты двух последовательных итераций не будут отличаться между собой на величину меньше заданной точности. Полученное решение будет удовлетворять принципу максимума.
Описанный простейший вариант итерационного процесса далеко не всегда сходится и чаще всего применяется с модификациями для улучшения сходимости, например методом Черноусько-Крылова [3, с. 1132–1139].
В статье сформулирована задача оптимизации дальности полета летательного аппарата, рассмотрены классы методов оптимизации (методы динамического программирования, прямые и косвенные методы) и выбраны пригодные для решения поставленной задачи. Рассмотрено математическое описание наиболее распространенных из выбранных классов методов.
Литература:
1. Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа. — M.: Наука, 1969. — 382с.
2. Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко. Математическая теория оптимальных процессов. М., Физматгиз, 1961.
3. Крылов И. А., Черноусько Ф. Л. О методе последовательных приближений для решения задач оптимального управления. // Ж. вычисл. матем. и матем. физ. 1962. Т. 2, № 6. С. 1132–1139.











