Цели урока:
Образовательные:
- повторить понятие рационального числа;
- повторить правила сложения, вычитания, умножения и деления рациональных чисел;
- повторить порядок действий в выражениях с целыми числами
- формировать умение выполнять действия в выражениях с рациональными числами
Развивающие:
- развивать внимание, речь, память, логическое мышление, самостоятельность.
Воспитательные:
- воспитывать стремление достигать поставленную цель; уверенности в себе, умение работать в коллективе.
Знать: правила сложения, вычитания, умножение и деление рациональных чисел
Уметь: выполнять действия в выражениях с рациональными числами
Тип урока: обобщение и систематизация знаний
Оборудование: экран, мультимедиа, презентация, раздаточный материал
|
№ п/п |
Этап урока |
Время |
Задачи этапа |
|
1 |
Организационный момент. |
1 мин |
Настроить учащихся на урок. |
|
2 |
Актуализация знаний. Повторение пройденного материала. |
8 мин |
Повторить правила сложения, вычитания, умножение и деление рациональных чисел |
|
3 |
Постановка проблемы |
10 мин |
Выведение алгоритма определения порядка действий в выражениях с рациональными числами |
|
4 |
Физкультминутка. |
3мин |
Снять утомление ребенка, обеспечить активный отдых и повысить умственную работоспособность учащихся. |
|
5 |
Закрепление изученного материала. |
15 мин |
Формировать умение применять алгоритм при определение порядка действий в числовом выражении и искать рациональные пути решения. |
|
6 |
Итог урока. |
5 мин |
- Подсчитать количество плюсов; - Самооценка - Рефлексия |
|
7 |
Домашнее задание |
3 мин |
|
Ход урока
1) Организационный момент.
2) Актуализация знаний. Повторение пройденного материала.
Фронтальный опрос:
- Какие числа вы изучили? (рациональные)
- Какие числа называются рациональными? (целые + дроби)
- Какие действия с рациональными числами вы умеете выполнять?
Нам сегодня необходимо повторить все действия с рациональными числами
Для того чтобы всё успеть повторить необходим план урока.
|
№ п/п |
Этап урока |
Время |
|
1 |
Организационный момент. |
1 мин |
|
2 |
Актуализация знаний. Повторение пройденного материала. |
8 мин |
|
3 |
Постановка проблемы |
10 мин |
|
4 |
Физкультминутка. |
3мин |
|
5 |
Закрепление изученного материала. |
15 мин |
|
6 |
Итог урока. |
5 мин |
|
7 |
Домашнее задание |
3 мин |
— Запишите в тетрадях тему сегодняшнего урока: «Все действия с рациональными числами»
— Сейчас вы разобьётесь на пять группы: четыре группы будут теоретиками, а одна практиками.
Теоретикам необходимо заполнить пропуски, используя знания теории, а практикам применить теоретические знания при решении задач. (На самостоятельную работу групп выделить 2–2,5 минуты. На проверку по 1 минуте на группу).
Iгруппа (теоретики): Закончите предложения
— Для сложения двух чисел одного знака нужно … (сложить их модули и поставить перед найденной суммой общий знак слагаемых)
— Для сложения двух чисел разного знака, имеющих разные модули, нужно …(вычесть из большего модуля меньший и поставить перед найденной разностью знак того слагаемого, чей модуль больше)
— Сумма двух противоположных чисел равна …(нулю) — Сумма рационального числа х и нуля равна … (х)
IIгруппа (теоретики): Закончите предложения
— Для нахождения разности рациональных чисел нужно … (к уменьшаемому прибавить число, противоположное вычитаемому)
— Если в алгебраической сумме перед скобками стоит знак «плюс», то … (скобки можно убрать, оставив все знаки внутри без изменения)
— Если в алгебраической сумме перед скобками стоит знак «минус», то … (скобки можно убрать, изменив все знаки внутри на противоположные)
IIIгруппа (теоретики): Закончите предложения
— Какой знак имеет произведение двух рациональных чисел одинаковых знаков?
— Какой знак имеет произведение двух рациональных чисел разных знаков?
— Чему равно произведение любого рационального числа и нуля? (х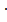 0 = 0)
0 = 0)
— Чему равно произведение любого рационального числа на -1? (х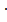 (-1) = — х)
(-1) = — х)
IVгруппа (теоретики): Закончите предложения
— Частным двух отличных от нуля рациональных чисел одного знака является …(положительное число)
— Частным двух отличных от нуля рациональных чисел разных знаков является …(отрицательное число)
— На нуль делить … (нельзя)
Vгруппа (практики): Письменно на листочках:
|
1) 1)-2,5 + (-6,4) = 2) 2)6,5 + (-8,8) = 3) 3)-7,1 + 7,1 = |
4) 4)- 9,8–4,9 = 5) 5) 6) 11 |
7) -1,1 8) |
9) 1: ( 10) 0: ( |
Проверить и подвести итоги (подсчитать количество плюсов и записать на полях)
3) Постановка проблемы: Чем мы с вами занимались? Что мы с вами повторили?
Вы обладаете достаточными знаниями, чтобы разобраться в одной проблемной ситуации:
Найдите значение выражения записанного на доске: (- 25–10): 5 +6 *(-3) =
— Чему равно значение выражения? (-25)
— Как узнали? (Выполнили действия)
— Я тоже решила это выражение, но у меня получился другой ответ (3).
— Как вы думаете почему? (Изменился порядок действий, т. е. действия выполнены в другой последовательности).
Какой вывод можно сделать из обсуждения нашей проблемной ситуации?
(Надо знать алгоритм для выполнения порядка действий)
На слайде записаны правила для выполнения порядка действий. Внимательно прочитайте их и пронумеруйте эти правила так, чтобы получился алгоритм для выполнения порядка действий.
Алгоритм
1. В выражения без скобок сначала выполняются умножение или деление, вычитание или сложение по порядку слева направо.
2. В выражениях со скобками — сначала выполняются действия в скобках, учитывая правило 1.
3. Если в числовом выражение есть степень числа, то сначала нужно записать её в виде числа и после этого приступить к выполнению остальных действий по уже сформулированным правилам.
— Как вы думаете, справедлив ли этот алгоритм для рациональных чисел?
(-2 * 0,5–1): (-0,4) + (-7,2). (Да) (на доске)
— Найдите значение этого выражения (1 ученик комментирует с места, остальные записывают в тетрадь)
Ответ -2,2
4) Физкультминутка
5) Закрепление
Задание 1. Правильно ли расставлен порядок действий в выражениях?
Почему вы так считаете. А как рациональнее?
1) 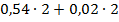 ; 2)
; 2) 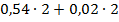 ; 3)
; 3) 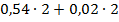
2) Рациональный способ: 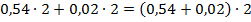
Задание 2. Выберите из данных числовых выражений те, порядок действий в которых таков: 1) сложение; 2) сложение; 3) умножение; 4) сложение; 5) деление; 6) вычитание.
а) 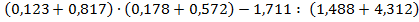 ;
;
б) 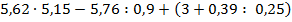 ;
;
в) 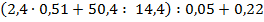 .
.
г) 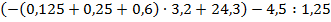 ;
;
Найдите значение этих выражений.
(выполнить взаимопроверку по слайду)
6) Подведение итогов (подсчитать количество плюсов)
- Самооценка (оценку, поставленную себе учеником, выставить в журнал)
- Рефлексия
|
1. На уроке я работал 2. Своей работой на уроке я 3. Урок для меня показался 4. За урок я 5. Мое настроение 6. Материал урока мне был 7. Домашнее задание мне кажется |
активно / пассивно доволен / не доволен коротким / длинным не устал / устал стало лучше / стало хуже понятен / не понятен полезен / бесполезен интересен / скучен легким / трудным интересным / неинтересным |
Литература:
1. Математика 6 класс.: учебник для общеобразоват. учреждений: в 2-х частях. Ч.1/С. А. Козлова, А. Г. Рубин.-2-е изд. — М.: Баласс, 2013 (Образовательная система «Школа 2100»
2. Математика 6 класс.: учебник для общеобразоват. учреждений: в 2-х частях. Ч.2/С. А. Козлова, А. Г. Рубин.-2-е изд. — М.: Баласс, 2013 (Образовательная система «Школа 2100»
3. http://festival.1september.ru







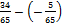 =
=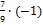 =
= (-1,1) =
(-1,1) =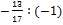 =
=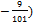 =
=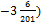 =
=