В статье показано, как с помощью компьютерной модели интерференции от двух точечных источников волн, предлагаемой автором, демонстрируется зависимость интерференционной картины от разности начальных фаз когерентных волн.
Ключевые слова:визуализация, компьютерная визуализация, компьютерное моделирование, модель, учебная компьютерная модель, интерференция, опыт Юнга, когерентные волны.
Эта статья является продолжением серии наших статей и других работ, опубликованных ранее [1; 2; 3; 4; 5; 6; 7; 9].
В учебной теории приводится формула для расчета координаты максимумов интерференционной картины (рис. 1):
xk,max = kyλ / d, k = 0, ±1, ±2, …,
где xk,max — координата максимума интенсивности, k — порядок максимума интенсивности, y — расстояние от источников до интерференционной картины (одномерного распределения интенсивности, представленного в виде графика), λ — длина волны, d — расстояние между источниками когерентных волн (d << y). Это условие получается из предположения того, что максимум интерференционной картины будет наблюдаться в данной точке пространства в том случае, если разность хода, приходящих в нее волн, равна целому числу длин волн (kλ) или четному числу длин полуволн (2kˑ λ/2). Иными словами, если колебания, созданные двумя волнами в данной точке, происходят в ней синфазно (разность их начальных фаз равна 2πn, где n — целое число), то в точке расположен максимум интенсивности результирующей волны. В точках, где находятся минимумы интерференционной картины эти колебания происходят в противофазе, то есть взаимно гасят друг друга. Разность начальных фаз колебаний в этом случае должна быть равна πn (n - нечетное число). Таким образом, если изменить начальную фазу одной из интерферирующих волн на π, то минимумы и максимумы интерференционной картины (функции I(x)) согласно теоретическим рассуждениям поменяются местами (рис. 1).
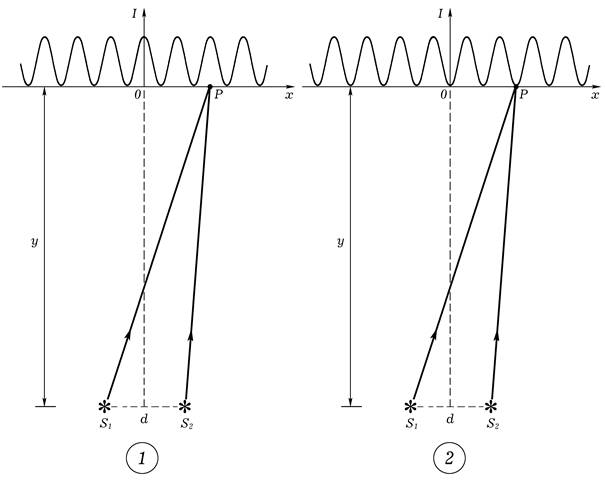
Рис. 1. Теоретические представления об интерференционной картине при изменении разности начальных фаз колебаний источников: 1 — разность начальных фаз волн равна 2πn (n = 0, ±1, ±2, …), 2 — разность начальных фаз волн равна πn (n = ±1, ±3, ±5,…)
Изменение интерференционной картины можно демонстрировать обучающимся с помощью компьютерной модели интерференции, созданной нами специально для изучения этого явления [4]. Это компьютерное приложение позволяет визуализировать распределение интенсивности результирующей волны на плоскости и вдоль прямой, параллельной отрезку, соединяющему источники волн. Демонстрация зависимости, о которой шла речь выше, может быть осуществлена следующим образом. Сначала обучающимся показывают картину распределения интенсивности, представленную на рис. 2. Обращают внимание на то, что в центре интерференционной картины расположен максимум интенсивности. Затем, меняя начальную фазу одной из волн, демонстрируют изменение интерференционной картины (рис. 3). Все остальные условия виртуального опыта при этом остаются неизменными. И наконец, когда разность фаз двух интерферирующих волн станет равной π, обращают внимание на то, что теперь в центре интерференционной картины расположен минимум интенсивности (рис. 3).
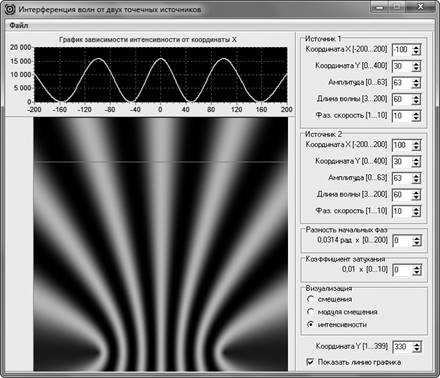
Рис. 2. Интерференционная картина, наблюдаемая при разности начальных фаз интерферирующих волн равной 0
Применение в обучении моделей, подобных той, что представлена в этой статье, способствует сближению естественно-научного образования и аутентичной педагогики [8, с. 120–137]. Учебные компьютерные модели предлагают новый метод исследования конкретного физического явления. В этом случае преподаватель осуществляет обучение, демонстрируя умение использовать носители информации, которые помогают активизировать процесс обучения. Этому способствует сама специфика физического явления, которая может быть такой, что какую-то информацию при непосредственном наблюдении явления получить невозможно или очень сложно. Чтобы создать такую модель, преподаватель должен осмыслить весь спектр возникающих познавательных проблем, которые ему необходимо будет решить совместно с обучающимися. Для обучающихся эта работа будет незаметна, но для преподавателя она очень важна, так как помогает избежать трудности, которые могут возникнуть в процессе обучения. Проектирование и создание модели облегчается, если преподаватель ясно представляет суть исследуемого явления и, основываясь на своем опыте, может предложить обучающимся удачные ориентиры, реализованные в модели чаще всего с помощью компьютерной визуализации.
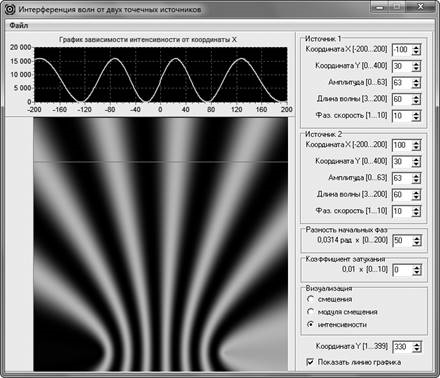
Рис. 3. Изменение интерференционной картины при изменении разности начальных фаз волн
Следует отметить, что при создании и использовании наглядных компьютерных моделей в обучении физике от преподавателя требуется умелая компиляция, а также оригинальное, а в некоторых случаях уникальное, соединение визуальных образов с теоретическими сведениями. Во многих решаемых физических задачах можно легко выделить эмпирическую составляющую имитационной модели и математическое описание явления. Но наибольшая ценность построенной модели определяется представленной в ней возможностью предсказывать поведение и развитие явления. Предложенный метод обучения объединяет традиционное (чаще всего репродуктивное) обучение и аутентичную технологию. Используя такое обучение, преподаватель выявляет сущность объекта исследования для обучающихся и раскрывает для них суть самого метода объяснения (чаще всего таким методом является метод научной визуализации). Объяснение преподавателя в этом случае может рассматриваться обучающимися как процедура собственной познавательной деятельности, а также как понимание через восприятие объяснения кого-то другого и дальнейшее освоение этого учебного материала. Говорят, что в этом случае обучающийся обращает метод объяснения на самого себя.
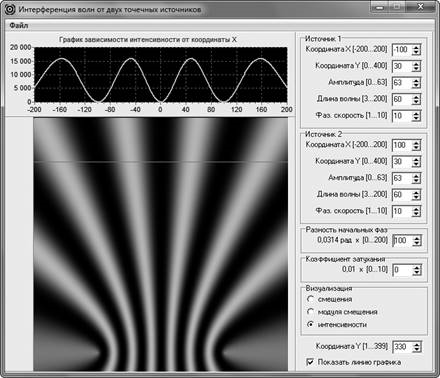
Рис. 4. Смена центрального максимума интерференционной картины на минимум при изменении разности начальных фаз волн на π
Литература:
1. Данилов О. Е. Демонстрация зависимости интерференционной картины от расстояния между двумя источниками волн с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2015. — № 1. — С. 15–18.
2. Данилов О. Е. Демонстрация зависимости распределения интенсивности интерферируемой волны вдоль прямой от расстояния между этой прямой и отрезком, соединяющим точечные источники когерентных волн, с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 16. — С. 15–19.
3. Данилов О. Е. Демонстрация явления интерференции волн от двух точечных источников с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 13. — С. 5–10.
4. Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 9. — С. 50–58.
5. Данилов О. Е. Компьютерная модель интерференции от двух точечных источников / О. Е. Данилов // Информатика: проблемы, методология, технологии: Материалы XI Международной научно-практической конференции, Воронеж, 10-11 февраля 2011 г.: в 3 т. Т. 3. Школа-конференция "Информатика в образовании". – Воронеж: Издательско-полиграфический центр Воронежского государственного университета, 2011. – С. 87-89.
6. Данилов О. Е. Компьютерное моделирование: Волновое уравнение. Численные методы решения физических задач. Borland Pascal. Учебно-методическое пособие / О. Е. Данилов. — Глазов: ГГПИ, 2009. — 24 с.
7. Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7. — С. 84–94.
8. Дахин А. Н. Моделирование компетентности участников образовательного процесса / А. Н. Дахин. — М.: НИИ школьных технологий, 2009. — 292 с.
9. Компьютерная модель интерференции / О. Е. Данилов. — Электрон. дан. — Сайты Google, 2011. — Режим доступа: https://sites.google.com/site/intercommod/. — Загл. с экрана.







