В статье рассматривается, как с помощью компьютерной модели интерференции от двух точечных источников когерентных волн, предлагаемой автором, демонстрируется зависимость интерференционной картины от длин этих волн.
Ключевые слова:визуализация, компьютерная визуализация, компьютерное моделирование, модель, учебная компьютерная модель, интерференция, опыт Юнга, когерентные волны.
Ранее нами уже были опубликованы статьи, посвященные учебной компьютерной модели интерференции волн от двух точечных источников [1; 2; 3; 4; 5; 6; 7]. Эта статья является их логическим продолжением.
Из учебной теории известна формула для расчета ширины максимумов интерференционной картины, полученной от двух точечных источников когерентных волн (рис. 1) [1]:
Δx= xk+1 — xk= yλ / d,
где k — номер интерференционного максимума, y — расстояние от отрезка, соединяющего источники волн; λ — длина волны; d — расстояние между источниками. Выражение получено аналитически при условии, что расстояние y >> d. Именно поэтому на графике, изображающем зависимость интенсивности интерферируемой волны I(x) от координаты x максимумы интенсивности имеют одинаковую ширину (рис. 1). Эта приближенная формула позволяет сделать вывод, согласно которому при изменении длины волны и неизменных расстояниях y и d, ширина интерференционных максимумов также будет изменяться. И эта зависимость ширины максимума от длины волны будет прямо пропорциональной. Иными словами, например, при увеличении длины волны в два раза ширина интерференционных максимумов, находящихся на прежнем расстоянии от источников когерентных волн, также увеличится в два раза (рис. 1). Следует отметить, что, на самом деле, если считать волны, распространяющиеся от точечных источников, сферическими, ширина максимумов в разных местах интерференционной картины будет различной, — она будет увеличивается по мере удаления от центрального (нулевого) максимума интенсивности волны при перемещении вдоль прямой, параллельной отрезку, соединяющему источники волн. Это будет хорошо заметно в случае расчета интерференционной картины с помощью компьютера и последующего вывода ее на экран. Тем не менее, вывод о том, что при увеличении длины волны ширина максимумов будет увеличиваться, является правильным.
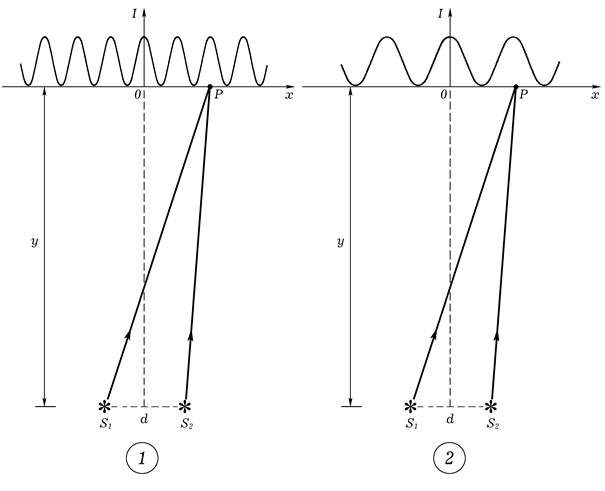
Рис. 1. Теоретические картины распределений интенсивности интерферируемой волны вдоль отрезка прямой, соответствующие разным длинам волн
В предыдущих наших статьях уже была описана компьютерная программа, моделирующая двумерную (плоскую) и одномерную картины распределения интенсивности интерферируемой волны в пространстве. Поэтому кратко рассмотрим, как с помощью нее можно демонстрировать учащимся изменение интерференционной картины при изменении длин интерферирующих волн. Сначала с помощью интерфейса программы устанавливают некоторые одинаковые значения длин волн, распространяющихся от источников. Наблюдают картины распределений (рис. 2). Отмечают, что максимумы на одномерном распределении (расположено в верхней части окна программы) неодинаковы по ширине. Кроме того, картина двумерного распределения позволяет говорить о том, что ширина каждого максимума увеличивается по мере удаления от источников.
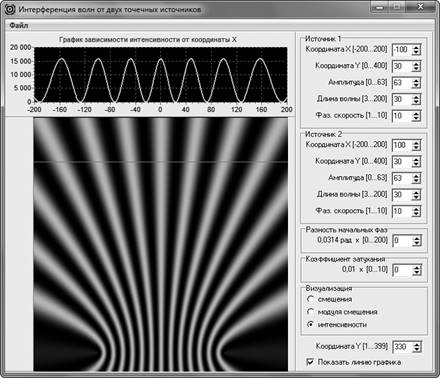
Рис. 2. Интерференционная картина
После этого, оставляя все параметры, кроме длин волн, неизменными, наблюдают новые картины двух распределений (рис. 3). Замечают, что ширина максимумов в том же месте пространства увеличивается примерно в такое же число раз, в какое была увеличена длина волны от каждого из источников.
Предлагаемая нами для изучения интерференции волн учебная компьютерная модель имеет несомненные преимущества перед обычными иллюстрациями в учебниках, так как обеспечивает лучшую наглядность, а также является интерактивной. Последнее ее качество позволяет организовать активное обучение, предполагающее модельное экспериментирование. Это, в свою очередь, развивает у учащихся навыки, необходимые для исследовательской деятельности.
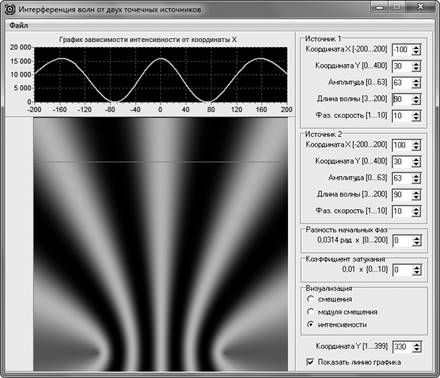
Рис. 3. Изменение вида интерференционной картины
Литература:
1. Данилов О. Е. Демонстрация зависимости интерференционной картины от расстояния между двумя источниками волн с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2015. — № 1. — С. 15–18.
2. Данилов О. Е. Демонстрация зависимости распределения интенсивности интерферируемой волны вдоль прямой от расстояния между этой прямой и отрезком, соединяющим точечные источники когерентных волн, с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 16. — С. 15–19.
3. Данилов О. Е. Демонстрация явления интерференции волн от двух точечных источников с помощью компьютерной модели / О. Е. Данилов // Молодой ученый. — 2014. — № 13. — С. 5–10.
4. Данилов О. Е. Изучение интерференции с помощью компьютерного моделирования / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 9. — С. 50–58.
5. Данилов О. Е. Компьютерная модель интерференции от двух точечных источников / О. Е. Данилов // Информатика: проблемы, методология, технологии: Материалы XI Международной научно-практической конференции, Воронеж, 10–11 февраля 2011 г.: в 3 т. Т. 3. Школа-конференция «Информатика в образовании». — Воронеж: Издательско-полиграфический центр Воронежского государственного университета, 2011. — С. 87–89.
6. Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7. — С. 84–94.
7. Компьютерная модель интерференции / О. Е. Данилов. — Электрон. дан. — Сайты Google, 2011. — Режим доступа: https://sites.google.com/site/intercommod/. — Загл. с экрана.







