Математическая статистика — это наука, изучающая количественные показатели развития общества и общественного производства. Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Статистическая информация — это числовые данные о массовых явлениях.
Предметом статистики являются размеры и количественные соотношения между массовыми общественными явлениями, закономерности их формирования, развития, взаимосвязи. Одной из основных задач статистики является обработка информации. Конечно, у статистики есть много и других задач: получение и хранение информации, выработка различных прогнозов, оценка их достоверности. Статистические данные применяются постоянно во всех сферах жизни, так же как и статистические методы, которые обеспечивают сбор необходимых данных. Основу статистики должны знать все люди, так как эта наука обучает, как собирать и систематизировать их, а также анализировать и делать выводы. В жизни подобные знаний могут пригодиться и не раз, причем на любой работе. Статистика помогает формировать наблюдательность, которая нужна при сборе информации. Информация должна быть качественной и достоверной, так как на основе нее придется принимать решения. Очень заметна польза статистики в экономике.
В результате работы со статистическими данными у учащихся формулируются представления о простейших статистических характеристиках; повторяются полученные знания по математике — вычислять моду, медиану, среднее арифметическое, размах числового ряда; показать прикладной характер математики к изучению окружающего мира; использовать возможностями электронных таблиц Excel, осуществлять поиск информации в Интернете.
Вначале урока необходимо повторить понятия математической статистики:
- Что такое размах числового ряда ряд? (Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.)
- Что характеризует размах?
- Что такое среднее арифметическое значение набора? (Частное от деления суммы этих чисел на число слагаемых.)
- Что такое медиана числового набора? (Число, стоящее посередине в упорядоченном по возрастанию ряду этих чисел, если их количество нечетно; полусумма чисел, стоящих на средних местах в упорядоченном наборе этих чисел, если их количество четно.)
- Мода числового набора? (Модой числового ряда называется число, которое встречается в ряду чаще других.)
- Сколько мод может иметь числовой ряд?
- Как упорядочить ряд чисел? (Записать числа так, чтобы каждое последующее число было не меньше предыдущего.)
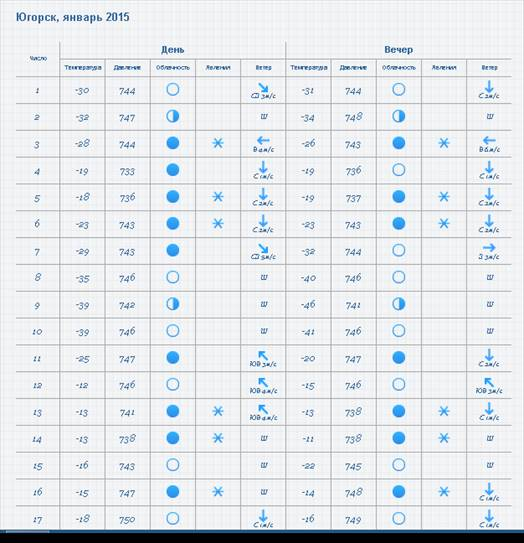
Статистические исследования можно применять при изучении погоды и климата. Например, можно использовать дневник погоды на сайте: http://beta.gismeteo.ru/diary/11965/2015/1/.
Таблица, скопированная с сайта, легко вставляется в электронную таблицу Excel. Эту таблицу легко обработать, ненужные столбцы можно удалить. Используя математические определения и формулы, легко рассчитать статистические данные: среднее арифметическое, размах, моду и медиану. В результате некоторых преобразований получаем следующую таблицу, в которой можно производить математические операции.
|
|
День |
Вечер |
|||
|
Число |
Температура |
Давление |
Температура |
Давление |
|
|
1 |
-30 |
744 |
-31 |
744 |
|
|
2 |
-32 |
747 |
-34 |
748 |
|
|
3 |
-28 |
744 |
-26 |
743 |
|
|
4 |
-19 |
733 |
-19 |
736 |
|
|
5 |
-18 |
736 |
-19 |
737 |
|
|
6 |
-23 |
743 |
-23 |
743 |
|
|
7 |
-29 |
743 |
-32 |
744 |
|
|
8 |
-35 |
746 |
-40 |
746 |
|
|
9 |
-39 |
742 |
-46 |
741 |
|
|
10 |
-39 |
746 |
-41 |
746 |
|
|
11 |
-25 |
747 |
-20 |
747 |
|
|
12 |
-12 |
746 |
-15 |
746 |
|
|
13 |
-13 |
741 |
-13 |
738 |
|
|
14 |
-13 |
738 |
-11 |
738 |
|
|
15 |
-16 |
743 |
-22 |
745 |
|
|
16 |
-15 |
747 |
-14 |
748 |
|
|
17 |
-18 |
750 |
-16 |
749 |
|
|
18 |
-7 |
742 |
-5 |
737 |
|
|
19 |
-2 |
735 |
-11 |
737 |
|
|
20 |
-17 |
743 |
-20 |
744 |
|
|
21 |
-18 |
742 |
-23 |
746 |
|
|
22 |
-22 |
756 |
-23 |
758 |
|
|
23 |
-25 |
765 |
-32 |
766 |
|
|
24 |
-20 |
768 |
-24 |
768 |
|
|
25 |
-13 |
759 |
-15 |
759 |
|
|
26 |
-8 |
752 |
-8 |
752 |
|
|
27 |
-8 |
752 |
-8 |
752 |
|
|
28 |
-8 |
746 |
-9 |
745 |
|
|
29 |
-9 |
747 |
-10 |
746 |
|
|
30 |
-6 |
749 |
-6 |
752 |
|
|
31 |
-8 |
754 |
-9 |
754 |
|
|
Мода |
-8 |
747 |
-23 |
746 |
|
|
746 |
|||||
|
743 |
|||||
|
Медиана |
-18 |
746 |
-19 |
746 |
|
|
Размах |
37 |
35 |
41 |
32 |
|
|
Среднее арифметическое |
-18,55 |
746,65 |
-20,16 |
746,94 |
|
Для нахождения Моды и Медианы дневной температуры используем соответствующие функции: =МОДА(C4:C34); =МЕДИАНА(C4:C34). Чтобы определить Размах нужно найти разность между максимальным и минимальным значением в числовом ряде: =МАКС(C4:C34)-МИН(C4:C34). Для нахождения Среднего значения применяем известную функцию: =СРЗНАЧ(C4:C34). В 3-ем столбце должно быть 3 значения Моды, функция находит 1 значение. Чтобы эти значения определить, можно воспользоваться вспомогательной таблицей, которая показывает сколько раз встречается число в данном ряду, т. е. применим формулу: =СЧЁТЕСЛИ(C$4:C$34;C4). Выделенные ячейки жёлтым цветом показывают сколько раз они повторяются. В 3 столбце мы наблюдаем 12 повторений, следовательно получаем 12/4=3 Моды.
|
Число |
День |
Вечер |
||
|
Температура |
Давление |
Температура |
Давление |
|
|
1 |
1 |
2 |
1 |
3 |
|
2 |
1 |
4 |
1 |
2 |
|
3 |
1 |
2 |
1 |
2 |
|
4 |
1 |
1 |
2 |
1 |
|
5 |
3 |
1 |
2 |
3 |
|
6 |
1 |
4 |
3 |
2 |
|
7 |
1 |
4 |
2 |
3 |
|
8 |
1 |
4 |
1 |
5 |
|
9 |
2 |
3 |
1 |
1 |
|
10 |
2 |
4 |
1 |
5 |
|
11 |
2 |
4 |
2 |
1 |
|
12 |
1 |
4 |
2 |
5 |
|
13 |
3 |
1 |
1 |
2 |
|
14 |
3 |
1 |
2 |
2 |
|
15 |
1 |
4 |
1 |
2 |
|
16 |
1 |
4 |
1 |
2 |
|
17 |
3 |
1 |
1 |
1 |
|
18 |
1 |
3 |
1 |
3 |
|
19 |
1 |
1 |
2 |
3 |
|
20 |
1 |
4 |
2 |
3 |
|
21 |
3 |
3 |
3 |
5 |
|
22 |
1 |
1 |
3 |
1 |
|
23 |
2 |
1 |
2 |
1 |
|
24 |
1 |
1 |
1 |
1 |
|
25 |
3 |
1 |
2 |
1 |
|
26 |
4 |
2 |
2 |
3 |
|
27 |
4 |
2 |
2 |
3 |
|
28 |
4 |
4 |
2 |
2 |
|
29 |
1 |
4 |
1 |
5 |
|
30 |
1 |
1 |
1 |
3 |
|
31 |
4 |
1 |
2 |
1 |
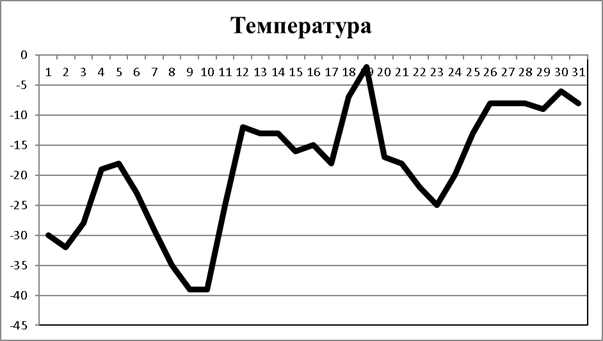
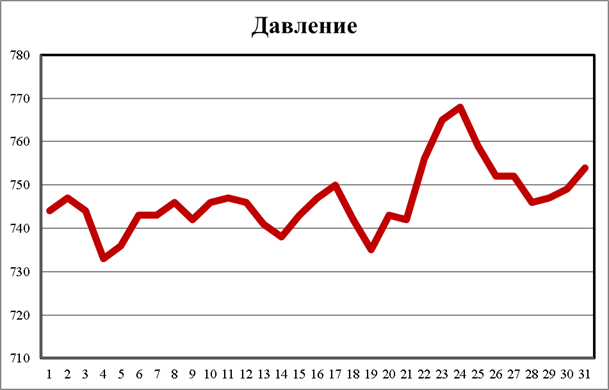
По готовой таблице дополнительно построить графики зависимости температуры, давления от времени.
Подводя итоги, хотелось бы сказать, что статистика — интересная и занимательная область математики. Статистические наблюдения используются практически везде, где только можно обусловить их применение. Вместе с тем, несмотря на обширную область применения, статистические наблюдения являются довольно сложным предметом и ошибки нередки. Однако, в целом наблюдения как предмет для рассмотрения представляют собой большой интерес. Необходимо организовать учебный процесс так, чтобы уроки информатики шли за уроками математики, т. е. те задачи, которые обучающиеся решали на математике, сразу решали и на уроках информатики с использованием современных технологий.
Из материалов Википедии https://ru.wikipedia.org/wiki/Югорск можно найти информацию о среднемесячных температурах города.
|
Климат Югорска |
|||||||||||||
|
Показатель |
Янв. |
Фев. |
Март |
Апр. |
Май |
Июнь |
Июль |
Авг. |
Сен. |
Окт. |
Нояб. |
Дек. |
Год |
|
Средняя температура, °C |
−16,5 |
−15,1 |
−8,1 |
−2 |
6,7 |
14,5 |
17,5 |
13,4 |
7,0 |
−0,4 |
−10,9 |
−15,1 |
−0,7 |
Мы видим, что температура в январе оказалась ниже среднемесячной. Статистические характеристики помогают выявить типичные показатели и особенности погоды. Если планировать путешествие — важно учесть информацию о погоде, в этом случае логично воспользоваться статистическими данными о погоде в районе предполагаемого маршрута. Погодная статистика существует во всём мире. Например:
http://philippine.ru/climate.html
http://www.holiday-weather.com/sharm_el_sheikh/averages/
http://www.windguru.cz/ru/historie_statsw.php
Литература:
1. https://ru.wikipedia.org/wiki/Югорск
2. http://beta.gismeteo.ru/diary/11965/2015/1/
3. Алгебра и начала математического анализа. 10–11 кл. Алимов А. Ш., Колягин Ю. М.
4. Информатика и информационные технологии. Учебник для 10–11 классов. Угринович Н. Д.







