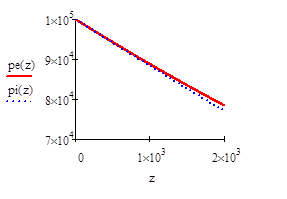Рассмотрим уравнение движения идеальной жидкости в форме Эйлера в инерциальной системе отсчета, без учета вращения Земли:
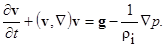(1)
Будем рассматривать плоский вертикальный случай, т. е. движение в плоскости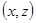 
. Запишем уравнение (1) в проекциях на оси координат:
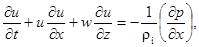(2)
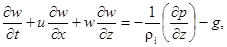(3)
В состоянии равновесия (статики атмосферы):
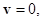
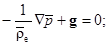
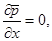
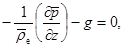
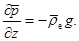(4)
Уравнение (4) есть уравнение статики атмосферы. Здесь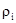 
– плотность воздушной частицы; 
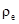– плотность окружающей воздушную частицу атмосферы. Параметры окружающей атмосферы мы рассматриваем как невозмущенное состояние.
Запишем уравнение состояния для окружающего сухого воздуха (уравнение Менделеева — Клапейрона):
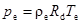(5)
Отсюда, взяв оператор «набла» с обеих частей равенства, получим
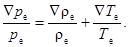
Для состояния статики атмосферы:
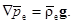
Тогда
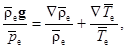
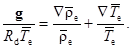
Предварительно предположим, что в состоянии статики атмосферы температура окружающей атмосферы изменяется не только с высотой 
, но и по оси 
по закону:
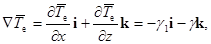(6)
где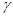 
— вертикальный градиент температуры окружающего воздуха по оси ; 
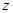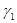— горизонтальный градиент температуры окружающего воздуха по оси .
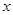Отсюда
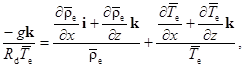
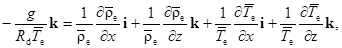
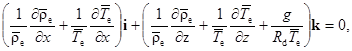
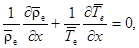
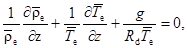
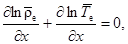
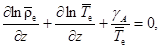
где
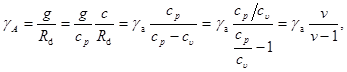
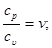
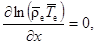
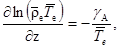
где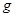 
— ускорение свободного падения; 
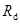– удельная газовая постоянная сухого воздуха.
Взяв производную по 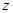от левого равенства и производную по 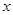от правого, и приравняв смешанные производные, получим, что в состоянии статики атмосферы
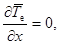
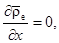
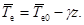
Отсюда следует, что в состоянии статики атмосферы горизонтальный градиент температуры (и плотности) равен нулю. Другими словами, наличие горизонтального градиента температуры (и плотности) всегда будет вызывать конвективное движение. Далее имеем
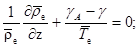
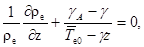
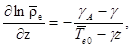(7)
где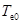 
— температура окружающего воздуха у земли в некоторой точке отсчета.
Найдем решение этого уравнения:
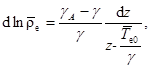
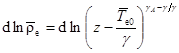
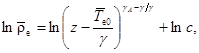
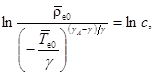
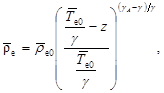
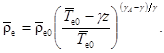(8)
Давление в окружающей атмосфере определяется барометрической формулой
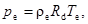
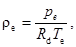
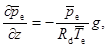
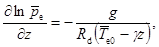
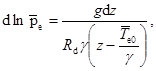
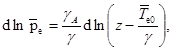
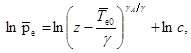
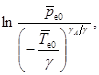
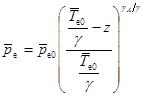
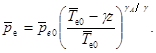(9)
Или приблизительно
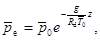
а давление воздуха, поднимающегося адиабатически, изменяется по закону
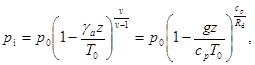
где 
— средняя температура окружающего подоблачного воздуха (рис. 1).
|
|
|
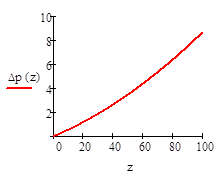
Рис. 1. Изменение давления с высотой в адиабатически поднимающемся воздухе и окружающей атмосфере
Из рисунков видно, что возмущение давления, вызванное адиабатическим подъемом воздуха, незначительно.
Литература:
1. Матвеев Л. Т. Физика атмосферы. — СПб: Гидрометеоиздат, 2000, 779 с.
